Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 4. Tính chất ba đường trung tuyến của tam giác
Đề kiểm tra 15 phút - Đề số 4 - Bài 4 - Chương 3 – Hình học 7
Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 4 - Chương 3 – Hình học 7
Đề bài
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC) trên tia AH lấy E sao cho H là trung điểm của AE. Trên tia đối của tia CB lấy F sao cho \(CF = BC\). Gọi M là trung điểm EB.
Chứng minh rằng: A, C, M thẳng hàng.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất đường trung tuyến trong tam giác
Lời giải chi tiết
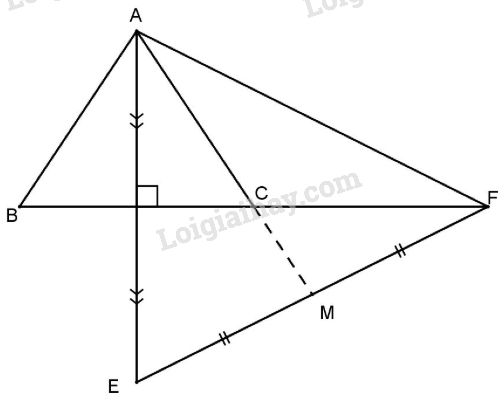
Xét hai tam giác vuông AHB và AHC có:
+) AH cạnh chung;
+) \(AB = AC\) (gt).
Do đó \(\Delta AHB = \Delta AHC\) (cạnh huyền - cạnh góc vuông)
\( \Rightarrow HB = HC = \dfrac{1 }{ 2}BC,\)
Mà \(CF = BC\) (gt) \( \Rightarrow HC = \dfrac{1 }{ 2}CF\).
Mặt khác H là trung điểm của AE (gt) nên FH là đường trung tuyến của \(\Delta A{\rm{E}}F\), lại có \(HC = \dfrac{1 }{2}CF\) (cmt), do đó C là trọng tâm của \(\Delta A{\rm{E}}F\).
Vì M là trung điểm của EF (gt) nên AM là trung tuyến của \(\Delta A{\rm{E}}F\).
Do đó AM phải đi qua trọng tâm C.
Hay ba điểm A, C, M thẳng hàng.
Loigiaihay.com
Bình luận
Chia sẻ
- Đề kiểm tra 15 phút - Đề số 5 - Bài 4 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 1 - Bài 4 - Chương 3 – Hình học 7
- Bài 30 trang 67 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
