Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 4. Tính chất ba đường trung tuyến của tam giác
Bài 24 trang 66 SGK Toán 7 tập 2
Cho hình bên. Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau :
Đề bài
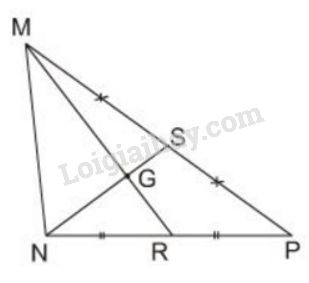
Cho hình \(25\). Hãy điền số thích hợp vào chỗ trống trong các đẳng thức sau:
a) \(MG = … MR ;\) \(GR = … MR ;\) \(GR = … MG\)
b) \(NS = ... NG;\) \(NS = …GS;\) \(NG = ... GS\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất ba đường trung tuyến của tam giác.
Lời giải chi tiết
Từ hình vẽ ta thấy: \(S, R\) lần lượt là trung điểm của \(MP;\,NP\) nên \(NS\) và \(MR\) là hai đường trung tuyến của tam giác \(MNP\).
\(G\) là giao của hai đường trung tuyến nên \(G\) là trọng tâm của \(ΔMNP\), do đó ta có thể điền như sau:
a) \(MG =\dfrac{2}{3} MR ;\) \(GR = \dfrac{1}{3} MR ;\) \(GR =\dfrac{1}{2} MG.\)
b) \(NS =\dfrac{3}{2} NG;\) \(NS =3GS;\) \(NG =2GS.\)
Ta chứng minh:
a) Vì \(G\) là trọng tâm của \(ΔMNP\) nên theo tính chất trọng tâm tam giác ta có:
\(\begin{array}{l}
\dfrac{{MG}}{{MR}} = \dfrac{2}{3} \Rightarrow MG = \dfrac{2}{3}MR\\
\Rightarrow GR = MR - MG = MR - \dfrac{2}{3}MR = \dfrac{1}{3}MR
\end{array}\)
Từ đó suy ra: \(\dfrac{{GR}}{{MG}} = \dfrac{{\dfrac{1}{3}MR}}{{\dfrac{2}{3}MR}}= \dfrac{1}{2} \)\(\Rightarrow GR = \dfrac{1}{2}MG\)
b) Vì \(G\) là trọng tâm của \(ΔMNP\) nên theo tính chất trọng tâm tam giác ta có:
\(\begin{array}{l}
\dfrac{{NG}}{{NS}} = \dfrac{2}{3} \Rightarrow NG = \dfrac{2}{3}NS;NS = \dfrac{3}{2}NG\\
\Rightarrow GS = NS - NG = NS - \dfrac{2}{3}NS = \dfrac{1}{3}NS\\
\Rightarrow NS = 3GS\\
\dfrac{{NG}}{{GS}} = \dfrac{{\dfrac{2}{3}NS}}{{\dfrac{1}{3}NS}} = 2 \Rightarrow NG = 2GS
\end{array}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 25 trang 67 SGK Toán 7 tập 2
- Bài 26 trang 67 SGK Toán 7 tập 2
- Bài 27 trang 67 SGK Toán 7 tập 2
- Bài 28 trang 67 SGK Toán 7 tập 2
- Bài 29 trang 67 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
