Đề khảo sát chất lượng đầu năm Toán 11- Đề số 8
Đề bài
Trong mặt phẳng $Oxy$, cho $A\left( {{x_A};{y_A}} \right)$ và ${\rm{ }}B\left( {{x_B};{y_B}} \right)$. Tọa độ của vectơ $\overrightarrow {AB} $ là
-
A.
$\overrightarrow {AB} = \left( {{y_A} - {x_A};{y_B} - {x_B}} \right)$.
-
B.
$\overrightarrow {AB} = \left( {{x_A} + {x_B};{y_A} + {y_B}} \right)$
-
C.
$\overrightarrow {AB} = \left( {{x_A} - {x_B};{y_A} - {y_B}} \right)$.
-
D.
$\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$.
Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?
-
A.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ cùng hướng
-
B.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ ngược hướng.
-
C.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ đối nhau.
-
D.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ bằng nhau.
-
A.
\(f\left( x \right) = - 8 - 4x\)
-
B.
\(f\left( x \right) = - 8 + 4x\)
-
C.
\(f\left( x \right) = 16 - 8x\)
-
D.
\(f\left( x \right) = 16 + 8x\)
Bạn An chọn một số nguyên, nhân số đó với 4 rồi trừ đi 30. Lấy kết quả có được nhân với 2 và cuối cùng trừ đi 10 thì được một số có hai chữ số. Số lớn nhất An có thể chọn được có hàng đơn vị bằng:
-
A.
\(8\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(2\)
Một công ty kinh chuẩn bị cho đợt khuyến mại nhằm mục đích thu hút khác hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên internet và truyền hình. Chi phí cho 1 phút quảng cáo trên internet là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Trang internet chỉ nhận phát các chương trình quảng cáo ngắn nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dì tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên internet. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên internet và truyền hình như thế nào để hiệu quả nhất?
-
A.
3 phút và 5 phút
-
B.
5 phút và 3 phút
-
C.
4 phút và 5 phút
-
D.
5 phút và 4 phút
Elip có độ dài trục lớn là 12, độ dài trục nhỏ là 8 có phương trình chính tắc là:
-
A.
\(\dfrac{{{x^2}}}{{36}} + \dfrac{{{y^2}}}{{16}} = 1\).
-
B.
\(\dfrac{{{x^2}}}{{144}} + \dfrac{{{y^2}}}{{64}} = 1\).
-
C.
\(\dfrac{{{x^2}}}{{12}} + \dfrac{{{y^2}}}{8} = 1\).
-
D.
\(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{36}} = 1\).
Khoảng cách từ điểm M(–2;2) đến đường thẳng Δ: \(5x - 12y + 8 = 0\) bằng
-
A.
\(\dfrac{2}{{13}}\)
-
B.
\(2\)
-
C.
\(13\)
-
D.
\(14\)
Trên mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C(-1;0). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC.
-
A.
(0;0)
-
B.
(1;0)
-
C.
(2;0)
-
D.
(3;0)
Trên đường tròn lượng giác, khẳng định nào sau đây là đúng?
-
A.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có một số đo.
-
B.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có $2$ số đo sao cho tổng của chúng bằng $2\pi $.
-
C.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có $2$ số đo hơn kém nhau $2\pi $.
-
D.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ có vô số số đo sai khác nhau $2\pi $.
Đường thẳng đi qua \(A( - 2;3)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 3} \right)\) có phương trình tham số là:
-
A.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 3 + 3t\end{array} \right.\,\,\)
-
B.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3 + 3t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 2 - 2t\\y = 3 - 3t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = 3 - 3t\end{array} \right.\)
-
A.
\(0 < m < 3\)
-
B.
\(m < 0\)
-
C.
\(m < 0\) hoặc \(m > 3\)
-
D.
\(m > 3\)
Điều kiện xác định của phương trình \(\dfrac{{\sqrt {x + 2} }}{x} = \dfrac{2}{{{x^2} + 3x - 4}}\) là
-
A.
\(x \in \left( { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\)
-
B.
\(x \in \left[ { - 2; + \infty } \right)\)
-
C.
\(x \in \left[ { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\)
-
D.
\(x \in \left[ { - 2; + \infty } \right]\backslash \left\{ {0,1} \right\}\)
Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh.

Tính số trung vị của bảng số liệu trên.
-
A.
8
-
B.
7,5
-
C.
7,3
-
D.
7
Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?
-
A.
32 giờ
-
B.
84 giờ
-
C.
60 giờ
-
D.
40 giờ
Với giá trị nào của n thì đẳng thức sau luôn đúng?
\(\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\cos 12x} } } = \cos \dfrac{x}{{2n}}\)\(\,\,0 < x < \dfrac{\pi }{{12}}\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(\dfrac{1}{3}\)
-
D.
\(3\)
Trong các khẳng định sau khẳng định nào đúng:
-
A.
\(\mathbb{R}\backslash \mathbb{Q} = \mathbb{N}\).
-
B.
${\mathbb{N}^*} \cup \mathbb{N} = \mathbb{Z}$.
-
C.
${\mathbb{N}^*} \cap \mathbb{Z} = \mathbb{Z}$.
-
D.
${\mathbb{N}^*} \cap \mathbb{Q} = {\mathbb{N}^*}$.
-
A.
\(y = - 2 + 3x\)
-
B.
\(y = \dfrac{2}{x}\)
-
C.
\(y = \sqrt {x + 3} \)
-
D.
\(y = - x + 2\)
-
A.
\({90^o}\)
-
B.
\({120^o}\)
-
C.
\({60^o}\)
-
D.
\({45^o}\)
Đường tròn có tâm trùng với gốc tọa độ, bán kính \(R = 1\) có phương trình là:
-
A.
\({x^2} + {\left( {y + 1} \right)^2} = 1.\)
-
B.
\({x^2} + {y^2} = 1.\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1.\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1.\)
-
A.
\({120^0}\)
-
B.
\({60^0}\)
-
C.
\({150^0}\)
-
D.
\({45^0}\)
Cho tam giác \(ABC\) có \(A\left( {2;4} \right),B\left( {5;0} \right),C\left( {2;1} \right).\) Điểm \(N\) thuộc đường trung tuyến \(BM\) của tam giác \(ABC\) và có hoành độ bằng \( - 1.\) Tung độ của điểm \(N\) bằng
-
A.
\( - 5.\)
-
B.
\(5.\)
-
C.
\(2.\)
-
D.
\(1.\)
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có $A\left( {3; - 4} \right),$ $B\left( {1;5} \right)$ và $C\left( {3;1} \right)$. Tính diện tích tam giác \(ABC\).
-
A.
\(10.\)
-
B.
$5.$
-
C.
$\sqrt {26} .$
-
D.
$2\sqrt 5 .$
-
A.
y = –4x + 9
-
B.
y = 3x – 12
-
C.
y = –3x + 16
-
D.
y = 4x – 11
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\), \(B\left( {4;6} \right)\), tìm tọa độ điểm \(M\) trên trục \(Oy\) sao cho diện tích \(\Delta MAB\) bằng 1.
-
A.
\(\left( {0;0} \right)\) và \(\left( { - 1;0} \right).\)
-
B.
\(\left( {0;0} \right)\) và \(\left( {0;\dfrac{4}{3}} \right).\)
-
C.
\(\left( {0; - 1} \right)\) và \(\left( {0;\dfrac{4}{3}} \right)\).
-
D.
\(\left( {0;\dfrac{2}{3}} \right)\) và \(\left( { - \dfrac{1}{2};0} \right)\).
Giá trị lớn nhất của biểu thức \(A = \dfrac{{{x^4} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}\) là
-
A.
\(1\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(0\)
-
D.
\(2\)
-
A.
\(\cos a + \cos b = 2\cos \dfrac{{a + b}}{2}.\cos \dfrac{{a - b}}{2}\).
-
B.
\(\sin a - \sin b = 2\cos \dfrac{{a + b}}{2}.\sin \dfrac{{a - b}}{2}\).
-
C.
\(\cos a - \cos b = 2\sin \dfrac{{a + b}}{2}.\sin \dfrac{{a - b}}{2}\).
-
D.
\(\sin a + \sin b = 2\sin \dfrac{{a + b}}{2}.\cos \dfrac{{a - b}}{2}\).
Cho \(a,\,\,b,\,\,c\) là độ dài ba cạnh của một tam giác. Mệnh đề nào sau đây không đúng?
-
A.
\({a^2} < ab + ac\)
-
B.
\(ab + bc > {b^2}\)
-
C.
\(b{}^2 + {c^2} < {a^2} + 2bc\)
-
D.
\(b{}^2 + {c^2} > {a^2} + 2bc\)
Mệnh đề nào sau đây sai? Đường thẳng \(\left( d \right)\) được xác định khi biết.
-
A.
Một vecto pháp tuyến hoặc một vec tơ chỉ phương.
-
B.
Hệ số góc và một điểm thuộc đường thẳng
-
C.
Một điểm thuộc \(\left( d \right)\) và biết \(\left( d \right)\) song song với một đường thẳng cho trước
-
D.
Hai điểm phân biệt thuộc \(\left( d \right)\).
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = 2{x^2} - mx + m\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) là
-
A.
\(( - \infty ;4]\)
-
B.
\(( - \infty ;2]\)
-
C.
\({\rm{[}}2; + \infty )\)
-
D.
\({\rm{[4}}; + \infty )\)
Tổng số nghiệm của phương trình \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\) bằng
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(1\)
Bất phương trình \(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \) có nghiệm là
-
A.
\( - 9 < x \le 4\)
-
B.
\( - 9 < x < 4\)
-
C.
\( - 9 < x < - 4\)
-
D.
\( - 4 < x < - 1\)
Lời giải và đáp án
Trong mặt phẳng $Oxy$, cho $A\left( {{x_A};{y_A}} \right)$ và ${\rm{ }}B\left( {{x_B};{y_B}} \right)$. Tọa độ của vectơ $\overrightarrow {AB} $ là
-
A.
$\overrightarrow {AB} = \left( {{y_A} - {x_A};{y_B} - {x_B}} \right)$.
-
B.
$\overrightarrow {AB} = \left( {{x_A} + {x_B};{y_A} + {y_B}} \right)$
-
C.
$\overrightarrow {AB} = \left( {{x_A} - {x_B};{y_A} - {y_B}} \right)$.
-
D.
$\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$.
Đáp án : D
Theo công thức tọa độ vectơ $\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)$.
Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?
-
A.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ cùng hướng
-
B.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ ngược hướng.
-
C.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ đối nhau.
-
D.
Hai vectơ $\overrightarrow b ,\overrightarrow c $ bằng nhau.
Đáp án : B
Vẽ hình và nhận xét dựa vào định nghĩa véc tơ đối.
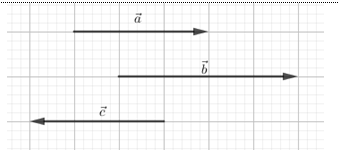
Quan sát hình vẽ trên ta thấy hai vectơ $\overrightarrow b ,\overrightarrow c $ ngược hướng.
Một số em có thể nhầm lẫn với đáp án C là sai vì hai véc tơ \(\overrightarrow b ,\overrightarrow c \) không cùng độ dài nên không đối nhau.
-
A.
\(f\left( x \right) = - 8 - 4x\)
-
B.
\(f\left( x \right) = - 8 + 4x\)
-
C.
\(f\left( x \right) = 16 - 8x\)
-
D.
\(f\left( x \right) = 16 + 8x\)
Đáp án : A
Dựa vào bảng xét dấu để tìm từng hệ số a, b của hàm số \(f\left( x \right) = ax + b\)
Xét phương trình:\(f\left( x \right) = 0 \Leftrightarrow ax + b = 0\) có nghiệm \(x = {x_0}\) thì:
+) Số \({x_1} > {x_0}\) thì \(f\left( {{x_1}} \right)\) cùng dấu với \(a.\)
+) Số \({x_1} < {x_0}\) thì \(f\left( {{x_1}} \right)\) trái dấu với \(a.\)
Gọi hàm số cần tìm có dạng \(f\left( x \right) = ax + b\)
Nhìn bảng xét dấu ta thấy với \({x_1} > - 2\) thì \(f\left( {{x_1}} \right) < 0 \Rightarrow \) hệ số \(a < 0\) \( \Rightarrow \) Loại B, D
Mặt khác với \(x = - 2\) thì \(f\left( x \right) = 0 \Rightarrow \) Chọn A.
Bạn An chọn một số nguyên, nhân số đó với 4 rồi trừ đi 30. Lấy kết quả có được nhân với 2 và cuối cùng trừ đi 10 thì được một số có hai chữ số. Số lớn nhất An có thể chọn được có hàng đơn vị bằng:
-
A.
\(8\)
-
B.
\(0\)
-
C.
\(1\)
-
D.
\(2\)
Đáp án : C
- Gọi số nguyên lớn nhất bạn An có thể chọn là \(x\) \(\left( {x \in \mathbb{Z}} \right)\).
- Tìm số \(A\) sau khi nhân số đó với 4 rồi trừ đi 30. Lấy kết quả có được nhân với 2 và cuối cùng trừ đi 100.
- Giải bất phương trình \(10 \le A \le 99\) và tìm \(x\) lớn nhất, từ đó suy ra hàng đơn vị của \(x\)
Gọi số nguyên lớn nhất bạn An có thể chọn là \(x\) \(\left( {x \in \mathbb{Z}} \right)\).
Theo bài ra ta có \(2\left( {4x - 30} \right) - 10\) là số có 2 chữ số.
\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}10 \le 2\left( {4x - 30} \right) - 10 \le 99\\ - 99 \le 2\left( {4x - 30} \right) - 10 \le - 10\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}20 \le 2\left( {4x - 30} \right) \le 109\\ - 89 \le 2\left( {4x - 30} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}10 \le 4x - 30 \le \dfrac{{109}}{2}\\ - \dfrac{{89}}{2} \le 4x - 30 \le 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}40 \le 4x \le \dfrac{{169}}{2}\\ - \dfrac{{29}}{2} \le 4x \le 30\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}10 \le x \le \dfrac{{169}}{8}\\ - \dfrac{{29}}{8} \le x \le \dfrac{{30}}{4}\end{array} \right.\end{array}\)
Vì \(x \in \mathbb{Z}\) và \(x\) là số lớn nhất nên \(x = 21\).
Vậy số lớn nhất An có thể chọn có hàng đơn vị bằng 1.
Một công ty kinh chuẩn bị cho đợt khuyến mại nhằm mục đích thu hút khác hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên internet và truyền hình. Chi phí cho 1 phút quảng cáo trên internet là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Trang internet chỉ nhận phát các chương trình quảng cáo ngắn nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dì tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên internet. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên internet và truyền hình như thế nào để hiệu quả nhất?
-
A.
3 phút và 5 phút
-
B.
5 phút và 3 phút
-
C.
4 phút và 5 phút
-
D.
5 phút và 4 phút
Đáp án : B
Bước 1: Gọi thời lượng công ty đặt quảng cáo trên internet là x (phút), trên truyền hình là y (phút).
Bước 2: Tìm các bất phương trình về chi phí quảng cáo, thời lượng.
Bước 3: Xác định bài toán tối ưu.
Bước 4: Vẽ miền nghiệm của hệ bất phương trình.
Bước 5: Tìm giá trị lớn nhất cho hiệu quả chung của quảng cáo.
Bước 1:
Gọi thời lượng công ty đặt quảng cáo trên internet là x (phút)\(\left( {x \ge 0} \right)\), trên truyền hình là y (phút)\(\left( {y \ge 0} \right)\).
Bước 2:
Chi phí cho việc quảng cáo là \(800000x + 4000000y\).
Vì mức chi phí tối đa là 16.000.000 đồng nên ta có bất phương trình:
\(\begin{array}{l}800000x + 4000000y \le 16000000\\ \Leftrightarrow x + 5y - 20 \le 0\end{array}\)
Do các điều kiện của internet và truyền hình nên ta có: \(x \ge 5,y \le 4\).
Hiệu quả chung của quảng cáo là \(x + 6y\).
Bước 3:
Bài toán trở thành: Xác định \(x,y\) sao cho \(M\left( {x;y} \right) = x + 6y\) đạt giá trị lớn nhất.
Với điều kiện \(\left\{ \begin{array}{l}x + 5y - 20 \le 0\\x \ge 5\\y \ge 0\\y \le 4\end{array} \right.\left( * \right)\)
Bước 4:
Xác định miền nghiệm của hệ (*):
Trong mặt phẳng tọa độ vẽ các đường thẳng \(\left( d \right):x + 5y - 20 = 0;\left( {d'} \right):x = 5;\)\(\left( {d''} \right):y = 4\).
Khi đó miền nghiệm của hệ (*) là phần mặt phẳng (tam giác) bị tô màu trên hình vẽ

Bước 5:
\(M\left( {x;y} \right) = x + 6y\) đạt giá trị lớn nhất tại một trong các điểm \(\left( {5;3} \right),\left( {5;0} \right),\left( {20;0} \right)\).
Ta có: \(M\left( {5;3} \right) = 23;M\left( {5;0} \right) = 5;\)\(M\left( {20;0} \right) = 20\).
Vậy nếu đặt thời lượng quảng cáo trên internet là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.
Elip có độ dài trục lớn là 12, độ dài trục nhỏ là 8 có phương trình chính tắc là:
-
A.
\(\dfrac{{{x^2}}}{{36}} + \dfrac{{{y^2}}}{{16}} = 1\).
-
B.
\(\dfrac{{{x^2}}}{{144}} + \dfrac{{{y^2}}}{{64}} = 1\).
-
C.
\(\dfrac{{{x^2}}}{{12}} + \dfrac{{{y^2}}}{8} = 1\).
-
D.
\(\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{36}} = 1\).
Đáp án : A
Phương trình chính tắc của elip có dạng \(\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\). Tìm\(a,b\)
- Elip có độ dài trục lớn bằng \(2a\)
- Elip có độ dài trục bé bằng \(2b\)
Độ dài trục lớn là 12, suy ra \(2a = 12\) hay \(a = 6\)
Độ dài trục nhỏ là 8, suy ra \(2b = 8\) hay \(b = 4\)
Vậy elip cần tìm là \(\dfrac{{{x^2}}}{{36}} + \dfrac{{{y^2}}}{{16}} = 1\)
Khoảng cách từ điểm M(–2;2) đến đường thẳng Δ: \(5x - 12y + 8 = 0\) bằng
-
A.
\(\dfrac{2}{{13}}\)
-
B.
\(2\)
-
C.
\(13\)
-
D.
\(14\)
Đáp án : B
Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\) là:
\(d\left( {{M_0};\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Khoảng cách từ điểm M(–2;2) đến đường thẳng Δ: \(5x - 12y + 8 = 0\):
\(d\left( {M;\Delta } \right) = \dfrac{{\left| { - 2.5 - 12.2 + 8} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \dfrac{{26}}{{13}} = 2\).
Trên mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C(-1;0). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC.
-
A.
(0;0)
-
B.
(1;0)
-
C.
(2;0)
-
D.
(3;0)
Đáp án : B
- Viết phương trình đường thẳng \(BC\), tham số hóa tọa độ điểm \(M \in BC\) theo tham số \(m\).
- Viết phương trình đường thẳng \(AM\) theo \(m\).
- Tính \(d\left( {B;AM} \right)\) và \(d\left( {C;AM} \right)\). Sử dụng công thức khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(ax + by + c = 0\) là \(d\left( {M;AB} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
- Để \({S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\), giải phương trình tìm \(m\).
Phương trình đường thẳng \(BC\) là \(y = 0\), vì \(M \in BC\) nên gọi \(M\left( {m;0} \right)\).
Ta có: \(\overrightarrow {AM} = \left( {m - 2; - 3} \right)\) nên \(\overrightarrow n = \left( {3;m - 2} \right)\) là 1 VTPT của đường thẳng \(AM\).
Phương trình đường thẳng \(AM\) là:
\(\begin{array}{l}3\left( {x - 2} \right) + \left( {m - 2} \right)\left( {y - 3} \right) = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 6 - 3m + 6 = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 3m = 0\end{array}\)
\(\begin{array}{l} \Rightarrow d\left( {B;AM} \right) = \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\\,\,\,\,\,\,d\left( {C;AM} \right) = \dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\end{array}\)
Ta có: \(\left\{ \begin{array}{l}{S_{\Delta MAB}} = \dfrac{1}{2}d\left( {B;AM} \right).AM\\{S_{\Delta MAC}} = \dfrac{1}{2}d\left( {C;AM} \right).AM\end{array} \right. \Rightarrow {S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\).
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }} = 2\dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\ \Leftrightarrow \left| {15 - 3m} \right| = 2\left| { - 3 - 3m} \right|\\ \Leftrightarrow \left[ \begin{array}{l}15 - 3m = - 6 - 6m\\15 - 3m = 6 + 6m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 7\\m = 1\end{array} \right.\end{array}\)
Vậy \(M\left( {1;0} \right)\) hoặc \(M\left( { - 7;0} \right)\).
Trên đường tròn lượng giác, khẳng định nào sau đây là đúng?
-
A.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có một số đo.
-
B.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có $2$ số đo sao cho tổng của chúng bằng $2\pi $.
-
C.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ chỉ có $2$ số đo hơn kém nhau $2\pi $.
-
D.
Cung lượng giác có điểm đầu $A$ và điểm cuối $B$ có vô số số đo sai khác nhau $2\pi $.
Đáp án : D
Sử dụng khái niệm cung lượng giác để xét tính đúng sai cho từng đáp án.
Đáp án A sai vì cung lượng giác có điểm đầu \(A\) điểm cuối \(B\) có vô số số đo hơn kém nhau \(k2\pi \).
Đáp án B sai vì chẳng hạn cung lượng giác \(AB\) có số đo \(\dfrac{\pi }{3}\) sẽ có các cặp số đo: \(\dfrac{\pi }{3};\dfrac{{5\pi }}{3}\) hay \(\dfrac{\pi }{3} + 6\pi ;\dfrac{{5\pi }}{3} - 6\pi \) hay nhũng cặp số đo khác mà tổng của chúng đều bằng \(2\pi \) chứ không phải chỉ \(1\).
Đáp án C sai vì cung lượng giác có điểm đầu \(A\) điểm cuối \(B\) có vô số số đo hơn kém nhau \(2\pi \).
Và do đó đáp án D đúng.
Đường thẳng đi qua \(A( - 2;3)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 3} \right)\) có phương trình tham số là:
-
A.
\(\left\{ \begin{array}{l}x = 2 - 2t\\y = - 3 + 3t\end{array} \right.\,\,\)
-
B.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3 + 3t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 2 - 2t\\y = 3 - 3t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = 3 - 3t\end{array} \right.\)
Đáp án : D
Phương trình tham số của đường thẳng \(\Delta \) đi qua \(A\left( {{x_0};{y_0}} \right)\) có VTCP \(\overrightarrow u = \left( {a;b} \right)\) là: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\)
-
A.
\(0 < m < 3\)
-
B.
\(m < 0\)
-
C.
\(m < 0\) hoặc \(m > 3\)
-
D.
\(m > 3\)
Đáp án : C
Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\)
Phương trình \(m{x^2} - 2\left( {m - 2} \right)x + 3 - m = 0\) có hai nghiệm trái dấu
\( \Leftrightarrow m\left( {3 - m} \right) < 0 \Leftrightarrow m\left( {m - 3} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m > 3\\m < 0\end{array} \right..\)
Điều kiện xác định của phương trình \(\dfrac{{\sqrt {x + 2} }}{x} = \dfrac{2}{{{x^2} + 3x - 4}}\) là
-
A.
\(x \in \left( { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\)
-
B.
\(x \in \left[ { - 2; + \infty } \right)\)
-
C.
\(x \in \left[ { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\)
-
D.
\(x \in \left[ { - 2; + \infty } \right]\backslash \left\{ {0,1} \right\}\)
Đáp án : C
Tỉm điều kiện xác định $\sqrt A $ xác định khi $A \ge 0$ và $\dfrac{1}{B}$ xác định khi $B \ne 0$.
Điều kiện xác định \(\left\{ {\begin{array}{*{20}{c}}{x + 2 \ge 0}\\{x \ne 0}\\{{x^2} + 3x - 4 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 1\\x \ne 0\\x \ne - 4\end{array} \right. \Leftrightarrow \) \(x \in \left[ { - 2; + \infty } \right)\backslash \left\{ {0,1} \right\}\).
Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh.

Tính số trung vị của bảng số liệu trên.
-
A.
8
-
B.
7,5
-
C.
7,3
-
D.
7
Đáp án : B
Với \(n = 2k\) (số chẵn) số liệu, số trung vị \({M_e} = \dfrac{{{x_k} + {x_{k + 1}}}}{2}\).
Do \(n = 20\) (số chẵn) nên \({M_e} = \dfrac{{{x_{10}} + {x_{11}}}}{2} = \dfrac{{7 + 8}}{2} = 7,5.\)
Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?
-
A.
32 giờ
-
B.
84 giờ
-
C.
60 giờ
-
D.
40 giờ
Đáp án : A
Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải bài toán.
Gọi số vòng tay bạn An làm là x (cái; \(x \in \mathbb{N}\)).
Số vòng đeo cổ bạn An làm là y (cái; \(y \in \mathbb{N}\)).
An bán x vòng tay được 40x ngàn đồng, bán y vòng đeo cổ được 80y ngàn đồng.
Vì An cần bán được ít nhất 400 ngàn đồng nên \(40x + 80y \ge 400\) hay \(x + 2y \ge 10\).
Mỗi tuần An bán được không quá 15 vòng tay và 4 vòng cổ nên \(x \le 15\) và \(y \le 4\).
Ta có hệ \(\left\{ \begin{array}{l}0 \le x \le 15\\0 \le y \le 4\\x + 2y \ge 10\end{array} \right.\).
Miền nghiệm của hệ là tứ giác ABCD với A(2;4), B(15;4), C(15;0), D(10;0).
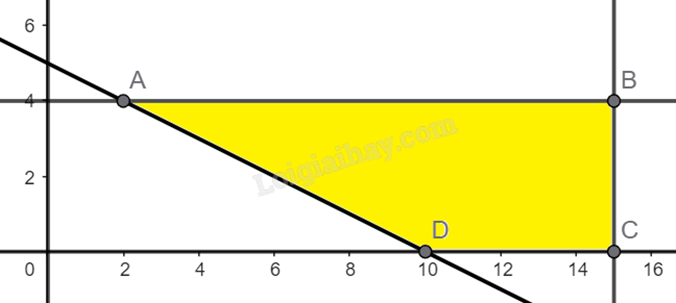
Số giờ An cần để làm x vòng tay và y vòng cổ là T = 4x + 6y.
Có T(2;4) = 4.2 + 6.4 = 32;
T(15;4) = 4.15 + 6.4 = 84;
T(15;0) = 4.15 + 6.0 = 60;
T(10;0) = 4.10 + 6.0 = 40.
Vậy số giờ tối thiểu An cần dùng trong tuần để bán được ít nhất 400 ngàn đồng là 32 giờ.
Với giá trị nào của n thì đẳng thức sau luôn đúng?
\(\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\cos 12x} } } = \cos \dfrac{x}{{2n}}\)\(\,\,0 < x < \dfrac{\pi }{{12}}\).
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(\dfrac{1}{3}\)
-
D.
\(3\)
Đáp án : C
Sử dụng công thức nhân đôi để biến đổi đẳng thức: \(\cos 2x = 2{\cos ^2}x - 1.\)
Hàm số \(y = \cos x\) là hàm số nghịch biến.
Ta có: \(0 < x < \dfrac{\pi }{{12}} \Rightarrow 0 < \dfrac{{3x}}{2} < 3x < 6x < \dfrac{\pi }{2} \Rightarrow 0 < \cos 6x < \cos 3x < \cos \dfrac{{3x}}{2} < 1\) (do hàm số \(y = \cos x\) là hàm số nghịch biến).
\(\begin{array}{l}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\cos 12x} } } \\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\left( {2{{\cos }^2}6x - 1} \right)} } } \\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + {{\cos }^2}6x - \dfrac{1}{2}} } } \\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {{{\cos }^2}6x} } } \\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\cos 6x} } \left( {do\cos 6x > 0} \right)\\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {\dfrac{1}{2} + \dfrac{1}{2}\left( {2{{\cos }^2}3x - 1} \right)} } \\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\sqrt {{{\cos }^2}3x} } \end{array}\)
\(\begin{array}{l} = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\cos 3x} \left( {do\cos 3x > 0} \right)\\ = \sqrt {\dfrac{1}{2} + \dfrac{1}{2}\left( {2{{\cos }^2}\dfrac{{3x}}{2} - 1} \right)} \\ = \sqrt {{{\cos }^2}\dfrac{{3x}}{2}} = \cos \dfrac{{3x}}{2}\left( {do\cos \dfrac{{3x}}{2} > 0} \right)\\ \Rightarrow \cos \dfrac{{3x}}{2} = \cos \dfrac{x}{{2n}}\left( 1 \right)\end{array}\)
Để (1) luôn đúng \( \Rightarrow \dfrac{{3x}}{2} = \dfrac{x}{{2n}} \Leftrightarrow n = \dfrac{1}{3}\)
Trong các khẳng định sau khẳng định nào đúng:
-
A.
\(\mathbb{R}\backslash \mathbb{Q} = \mathbb{N}\).
-
B.
${\mathbb{N}^*} \cup \mathbb{N} = \mathbb{Z}$.
-
C.
${\mathbb{N}^*} \cap \mathbb{Z} = \mathbb{Z}$.
-
D.
${\mathbb{N}^*} \cap \mathbb{Q} = {\mathbb{N}^*}$.
Đáp án : D
Xét tính đúng sai của mỗi đáp án dựa vào các phép toán giao, hợp, hiệu các tập hợp.
A sai vì \(\mathbb{R}\backslash \mathbb{Q} = I\)
B sai vì ${\mathbb{N}^*} \subset \mathbb{N} \Rightarrow {\mathbb{N}^*} \cup \mathbb{N} = \mathbb{N}$
C sai vì ${\mathbb{N}^*} \subset \mathbb{Z} \Rightarrow {\mathbb{N}^*} \cap \mathbb{Z} = {\mathbb{N}^*}$
D đúng do ${\mathbb{N}^*} \subset \mathbb{Q} \Rightarrow {\mathbb{N}^*} \cap \mathbb{Q} = {\mathbb{N}^*}$
-
A.
\(y = - 2 + 3x\)
-
B.
\(y = \dfrac{2}{x}\)
-
C.
\(y = \sqrt {x + 3} \)
-
D.
\(y = - x + 2\)
Đáp án : A
Hàm số: \(y = ax + b\,\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)
+) Xét đáp án A: \(y = - 2 + 3x\) có \(a = 3 > 0 \Rightarrow \) hàm số đồng biến trên \(\mathbb{R}.\)
-
A.
\({90^o}\)
-
B.
\({120^o}\)
-
C.
\({60^o}\)
-
D.
\({45^o}\)
Đáp án : A
Sử dụng công thức biến tổng thành tích và công thức lượng giác của các cung đặc biệt để biến đổi dữ kiện đề bài, kết hợp định lý tổng 3 góc trong tam giác để kết luận.
\(\sin A + \sin B = \cos A + \cos B \Leftrightarrow \sin \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2} = \cos \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2}\,\,\,\,\left( 1 \right)\)
TH1: \(\cos \dfrac{{A - B}}{2} = 0 \Rightarrow \dfrac{{A - B}}{2} = {90^o} \Rightarrow A - B = {180^o} = A + B + C \Leftrightarrow 2B + C = 0\) vô lý
TH2: \(\cos \dfrac{{A - B}}{2} \ne 0\) khi đó \(\left( 1 \right) \Leftrightarrow \sin \dfrac{{A + B}}{2} = \cos \dfrac{{A + B}}{2} \Leftrightarrow \sin \dfrac{{A + B}}{2} = \sin \dfrac{C}{2}\,\,\,\,\left( {do\,\,\,\dfrac{{A + B}}{2} + \dfrac{C}{2} = {{90}^o}} \right)\)
\( \Rightarrow \dfrac{{A + B}}{2} = \dfrac{C}{2} \Leftrightarrow A + B = C \Leftrightarrow {180^o} - C = C \Leftrightarrow 2C = {180^o} \Leftrightarrow C = {90^o}\)
Đường tròn có tâm trùng với gốc tọa độ, bán kính \(R = 1\) có phương trình là:
-
A.
\({x^2} + {\left( {y + 1} \right)^2} = 1.\)
-
B.
\({x^2} + {y^2} = 1.\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1.\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1.\)
Đáp án : B
Áp dụng cách viết phương trình đường tròn có tâm tâm \(I(a;b)\) và bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
\(\left( C \right):\left\{ \begin{array}{l}I\left( {0;0} \right)\\R = 1\end{array} \right. \) \( \to \left( C \right):{(x-0)^2} + {(y-0)^2} = 1 \) \(\to \left( C \right):{x^2} + {y^2} = 1.\)
-
A.
\({120^0}\)
-
B.
\({60^0}\)
-
C.
\({150^0}\)
-
D.
\({45^0}\)
Đáp án : A
Ta có: ABCD là hình chữ nhật nên ta có: AB = DC = a.
\(\begin{array}{l}\angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {DC} } \right) = \angle \left( {\overrightarrow {CA} ,\,\,\overrightarrow {Cx} } \right) = \angle ACx = {180^0} - \angle ACD.\\ \Rightarrow \cos \angle ACD = \dfrac{{AD}}{{AC}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\end{array}\)
\(\begin{array}{l} \Rightarrow \angle ACD = {60^0}\\ \Rightarrow \angle ACx = {180^0} - {60^0} = {120^0}.\end{array}\)
Cho tam giác \(ABC\) có \(A\left( {2;4} \right),B\left( {5;0} \right),C\left( {2;1} \right).\) Điểm \(N\) thuộc đường trung tuyến \(BM\) của tam giác \(ABC\) và có hoành độ bằng \( - 1.\) Tung độ của điểm \(N\) bằng
-
A.
\( - 5.\)
-
B.
\(5.\)
-
C.
\(2.\)
-
D.
\(1.\)
Đáp án : B
Tìm tọa độ trung điểm \(M\) của \(AC\) sau đó viết phương trình đường thẳng \(BM.\)
Thay hoành độ điểm \(N\) vào phương trình đường thẳng \(BM\) để tìm tung độ điểm \(N.\)
Ta có: \(M\) là trung điểm của \(AC\) suy ra \(M\left( {2;\dfrac{5}{2}} \right).\)
Phương trình đường trung tuyến \(BM\) đi qua hai điểm \(B\left( {5;0} \right)\) và \(M\left( {2;\dfrac{5}{2}} \right)\) là:
\(\begin{array}{l}\dfrac{{x - 5}}{{2 - 5}} = \dfrac{y}{{\dfrac{5}{2}}} \Leftrightarrow \dfrac{5}{2}\left( {x - 5} \right) = - 3y\\ \Leftrightarrow 5x - 25 + 6y = 0 \Leftrightarrow 5x + 6y - 25 = 0.\end{array}\)
Điểm \(N\) thuộc đường trung tuyến \(BM\) của \(\Delta ABC\) và có hoành độ bằng \( - 1\)
\( \Rightarrow 5.\left( { - 1} \right) + 6{y_N} - 25 = 0 \Rightarrow {y_N} = 5.\)
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có $A\left( {3; - 4} \right),$ $B\left( {1;5} \right)$ và $C\left( {3;1} \right)$. Tính diện tích tam giác \(ABC\).
-
A.
\(10.\)
-
B.
$5.$
-
C.
$\sqrt {26} .$
-
D.
$2\sqrt 5 .$
Đáp án : B
- Tính độ dài \(BC\) và chiều cao \({h_A} = d\left( {A,BC} \right)\)
- Công thức diện tích \({S_\Delta } = \dfrac{1}{2}BC.{h_A}\)
Cách 1:
+) Viết phương trình \(BC\):
Ta có: \(\overrightarrow {BC} = \left( {2; - 4} \right)\) nên \(\overrightarrow {{u_{BC}}} = \dfrac{1}{2}\overrightarrow {BC} = \left( {1; - 2} \right)\) là VTCP của \(BC\), do đó \(\overrightarrow {{n_{BC}}} = \left( {2;1} \right)\).
Đường thẳng \(BC\) đi qua \(B\left( {1;5} \right)\) và nhận \(\overrightarrow {{n_{BC}}} = \left( {2;1} \right)\) làm VTPT nên: \(BC:2\left( {x - 1} \right) + 1\left( {y - 5} \right) = 0\) hay \(BC:2x + y - 7 = 0\).
Suy ra $\left\{ \begin{array}{l}A\left( {3; - 4} \right)\\B\left( {1;5} \right),\,C\left( {3;1} \right)\end{array} \right. \to \left\{ \begin{array}{l}A\left( {3; - 4} \right)\\BC = 2\sqrt 5 \\BC:2x + y - 7 = 0\end{array} \right. \to \left\{ \begin{array}{l}BC = 2\sqrt 5 \\{h_A} = d\left( {A;BC} \right) = \sqrt 5 \end{array} \right.$
$ \to {S_{ABC}} = \dfrac{1}{2}.2\sqrt 5 .\sqrt 5 = 5.$
Các em có thể sử dụng công thức: ${S_{\Delta ABC}} = \dfrac{1}{2}\sqrt {A{B^2}.A{C^2} - {{\left( {\overrightarrow {AB} \cdot \overrightarrow {AC} } \right)}^2}} .$
-
A.
y = –4x + 9
-
B.
y = 3x – 12
-
C.
y = –3x + 16
-
D.
y = 4x – 11
Đáp án : C
- Giải phương trình hoành độ giao điểm để tìm tọa độ các điểm A, B.
- Gọi phương trình đường thẳng AB là y = ax + b. Thay tọa độ các điểm A, B vào và tìm a, b.
Xét phương trình hoành độ giao điểm:
\(\begin{array}{l}\,\,\,\,\,\,3{x^2} - 2 = 2{x^2} - x + 4\\ \Leftrightarrow {x^2} + x - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\end{array}\)
Với x = 2 thì y = 10 => A(2;10).
Với x = -3 thì y = 25 => B(-3;25).
Gọi phương trình đường thẳng AB là y = ax + b.
Vì \(A \in AB\) nên 10 = 2a + b.
Vì \(B \in AB\) nên 25 = -3a + b.
Ta có hệ phương trình
\(\left\{ \begin{array}{l}2a + b = 10\\ - 3a + b = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\b = 16\end{array} \right.\)
Vậy phương trình đường thẳng AB là y = –3x + 16.
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường thẳng đi qua hai điểm \(A\left( {1;2} \right)\), \(B\left( {4;6} \right)\), tìm tọa độ điểm \(M\) trên trục \(Oy\) sao cho diện tích \(\Delta MAB\) bằng 1.
-
A.
\(\left( {0;0} \right)\) và \(\left( { - 1;0} \right).\)
-
B.
\(\left( {0;0} \right)\) và \(\left( {0;\dfrac{4}{3}} \right).\)
-
C.
\(\left( {0; - 1} \right)\) và \(\left( {0;\dfrac{4}{3}} \right)\).
-
D.
\(\left( {0;\dfrac{2}{3}} \right)\) và \(\left( { - \dfrac{1}{2};0} \right)\).
Đáp án : B
Gọi M theo 1 chữ, từ diện tích \(\Delta MAB\) bằng 1 viết phương trình tìm M.
Gọi \(M\left( {0;m} \right) \in Oy;\,\,AB = \sqrt {{{\left( {4 - 1} \right)}^2} + {{\left( {6 - 2} \right)}^2}} = 5.\)
Có \({S_{\Delta MAB}} = \dfrac{1}{2}d\left( {M,AB} \right).AB\) \( \Leftrightarrow 1 = \dfrac{1}{2}.d\left( {M,AB} \right).5 \Leftrightarrow d\left( {M,AB} \right) = \dfrac{2}{5}\)
\(\overrightarrow {AB} = \left( {3;4} \right) \Rightarrow \overrightarrow n = \left( {4; - 3} \right)\) là 1 VTPT của AB.
\( \Rightarrow \) Phương trình AB: \(4\left( {x - 1} \right) - 3\left( {y - 2} \right) = 0 \Leftrightarrow 4x - 3y + 2 = 0\)
\( \Rightarrow d\left( {M,AB} \right) = \dfrac{{\left| { - 3m + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }}\)\( \Leftrightarrow \dfrac{2}{5} = \dfrac{{\left| { - 3m + 2} \right|}}{5} \Leftrightarrow \left| { - 3m + 2} \right| = 2\)
\( \Leftrightarrow \left[ \begin{array}{l} - 3m + 2 = 2\\ - 3m + 2 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0 \Rightarrow M\left( {0;0} \right)\\m = \dfrac{4}{3} \Rightarrow M\left( {0;\dfrac{4}{3}} \right)\end{array} \right.\)
Giá trị lớn nhất của biểu thức \(A = \dfrac{{{x^4} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}}\) là
-
A.
\(1\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(0\)
-
D.
\(2\)
Đáp án : A
\(A > 0\) nên \(A\) lớn nhất khi \(\dfrac{1}{A}\) nhỏ nhất và ngược lại.
Với mọi \(x \in \mathbb{R}\) ta có: \(\left. \begin{array}{l}{x^4} + 1 > 0\\{\left( {{x^2} + 1} \right)^2} > 0\end{array} \right\}\)\( \Rightarrow A = \dfrac{{{x^4} + 1}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{A} = \dfrac{{{{\left( {{x^2} + 1} \right)}^2}}}{{{x^4} + 1}}= \dfrac{{{x^4} + 2{x^2} + 1}}{{{x^4} + 1}}\\\,= 1 + \dfrac{{2{x^2}}}{{{x^4} + 1}}\end{array}\)
Ta có: \(\left\{ \begin{array}{l}2{x^2} \ge 0\\{x^4} + 1 > 0\end{array} \right.\) với mọi \(x \in \mathbb{R}\)
\( \Rightarrow \dfrac{{2{x^2}}}{{{x^4} + 1}} \ge 0\) với mọi \(x \in \mathbb{R}\)
\( \Rightarrow 1 + \dfrac{{2{x^2}}}{{{x^4} + 1}} \ge 1\) với mọi \(x \in \mathbb{R}\)
\(\min \dfrac{1}{A} = 1 \Leftrightarrow x = 0\)
Vậy \(\max A = 1 \Leftrightarrow x = 0\).
-
A.
\(\cos a + \cos b = 2\cos \dfrac{{a + b}}{2}.\cos \dfrac{{a - b}}{2}\).
-
B.
\(\sin a - \sin b = 2\cos \dfrac{{a + b}}{2}.\sin \dfrac{{a - b}}{2}\).
-
C.
\(\cos a - \cos b = 2\sin \dfrac{{a + b}}{2}.\sin \dfrac{{a - b}}{2}\).
-
D.
\(\sin a + \sin b = 2\sin \dfrac{{a + b}}{2}.\cos \dfrac{{a - b}}{2}\).
Đáp án : C
Sử dụng công thức lượng giác biến tổng thành tích.
Ta có: \(\cos a - \cos b = - 2\sin \dfrac{{a + b}}{2}\sin \dfrac{{a - b}}{2}\)
Vậy C sai.
Cho \(a,\,\,b,\,\,c\) là độ dài ba cạnh của một tam giác. Mệnh đề nào sau đây không đúng?
-
A.
\({a^2} < ab + ac\)
-
B.
\(ab + bc > {b^2}\)
-
C.
\(b{}^2 + {c^2} < {a^2} + 2bc\)
-
D.
\(b{}^2 + {c^2} > {a^2} + 2bc\)
Đáp án : D
Biến đổi các mệnh đề và áp dụng bất đẳng thức tam giác.
\(a,\,\,b,\,\,c\) là độ dài ba cạnh của một tam giác thì \(a > 0,\,\,b > 0,\,\,c > 0\).
Bất đẳng thức tam giác: \(\left\{ \begin{array}{l}a + b > c\\a + c > b\\b + c > a\end{array} \right.\)
Vì \(a,\,\,b,\,\,c\) là độ dài ba cạnh của một tam giác nên \(a > 0,\,\,b > 0,\,\,c > 0\).
Áp dụng bất đẳng thức tam giác ta có: \(\left\{ \begin{array}{l}a + b > c\\a + c > b\\b + c > a\end{array} \right.\)
+) Xét \({a^2} < ab + ac\)\( \Leftrightarrow {a^2} < a\left( {b + c} \right)\) \( \Leftrightarrow a < b + c\,\,\,\,\left( {tm} \right)\)
\( \Rightarrow \) Đáp án A đúng.
+) Xét \(ab + bc > {b^2}\) \( \Leftrightarrow b\left( {a + c} \right) > {b^2}\)\( \Leftrightarrow a + c > b\,\,\,\left( {tm} \right)\)
\( \Rightarrow \) Đáp án B đúng.
+) Xét \(b{}^2 + {c^2} < {a^2} + 2bc\)\( \Leftrightarrow b{}^2 + {c^2} - 2bc < {a^2}\)\( \Leftrightarrow {\left( {b - c} \right)^2} < {a^2}\)
\( \Leftrightarrow (b - c - a)(b-c+a)<0 \left( {tm} \right)\)
\( \Rightarrow \) Đáp án C đúng.
+) Xét \(b{}^2 + {c^2} > {a^2} + 2bc\)
\(\begin{array}{l} \Leftrightarrow b{}^2 + {c^2} - 2bc > {a^2}\\ \Leftrightarrow {\left( {b - c} \right)^2} > {a^2}\\ \Leftrightarrow |b - c| > a\left( {ktm} \right)\end{array}\)
\( \Rightarrow \) Đáp án D sai.
Mệnh đề nào sau đây sai? Đường thẳng \(\left( d \right)\) được xác định khi biết.
-
A.
Một vecto pháp tuyến hoặc một vec tơ chỉ phương.
-
B.
Hệ số góc và một điểm thuộc đường thẳng
-
C.
Một điểm thuộc \(\left( d \right)\) và biết \(\left( d \right)\) song song với một đường thẳng cho trước
-
D.
Hai điểm phân biệt thuộc \(\left( d \right)\).
Đáp án : A
Nếu chỉ có vecto pháp tuyến hoặc một vecto chỉ phương thì thiếu điểm đi qua để viết phương trình đường thẳng.
Tập hợp các giá trị của tham số \(m\) để hàm số \(y = 2{x^2} - mx + m\) đồng biến trên khoảng \(\left( {1; + \infty } \right)\) là
-
A.
\(( - \infty ;4]\)
-
B.
\(( - \infty ;2]\)
-
C.
\({\rm{[}}2; + \infty )\)
-
D.
\({\rm{[4}}; + \infty )\)
Đáp án : A
- Hàm số \(y = a{x^2} + bx + c\,\,\left( {a > 0} \right)\) đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\).
- Hàm số \(y = 2{x^2} - mx + m\) đồng biến trên \(\left( {\dfrac{m}{4}; + \infty } \right)\) nên để hàm số đồng biến trên \(\left( {1; + \infty } \right)\) thì \(\left( {1; + \infty } \right) \subset \left( {\dfrac{m}{4}; + \infty } \right)\)
Hàm số \(y = 2{x^2} - mx + m\) đồng biến trên \(\left( {\dfrac{m}{4}; + \infty } \right)\) nên để hàm số đồng biến trên \(\left( {1; + \infty } \right)\) thì \(\left( {1; + \infty } \right) \subset \left( {\dfrac{m}{4}; + \infty } \right)\)
\( \Rightarrow \dfrac{m}{4} \le 1 \Leftrightarrow m \le 4\).
Vậy \(m \in \left( { - \infty ;4} \right]\).
Tổng số nghiệm của phương trình \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\) bằng
-
A.
\(3\)
-
B.
\(2\)
-
C.
\(0\)
-
D.
\(1\)
Đáp án : A
Tìm điều kiện xác định.
Biến đổi và giải phương trình bằng phương pháp đưa về phương trình tích.
ĐK: \(x \ge \dfrac{{ - 7}}{2}\)
Ta có \(\left( {x - 2} \right)\sqrt {2x + 7} = {x^2} - 4\)
\(\begin{array}{l} \Leftrightarrow \left( {x - 2} \right)\sqrt {2x + 7} = \left( {x - 2} \right)\left( {x + 2} \right)\\ \Leftrightarrow \left( {x - 2} \right)\left[ {\sqrt {2x + 7} - \left( {x + 2} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\sqrt {2x + 7} = x + 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}2x + 7 = {\left( {x + 2} \right)^2}\\x \ge - 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\2x + 7 = {x^2} + 4x + 4\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\{x^2} + 2x - 3 = 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\\left\{ \begin{array}{l}x \ge - 2\\\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = 1\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow \) Tổng hai nghiệm của phương trình là: \(2 + 1 = 3.\)
Bất phương trình \(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \) có nghiệm là
-
A.
\( - 9 < x \le 4\)
-
B.
\( - 9 < x < 4\)
-
C.
\( - 9 < x < - 4\)
-
D.
\( - 4 < x < - 1\)
Đáp án : B
Đặt \(\sqrt {{x^2} + 5x + 28} = t\left( {t > 0} \right)\)
Giải bất phương trình ẩn t rồi tìm x.
TXĐ: \(D = \mathbb{R}\)
\(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \)\( \Leftrightarrow {x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} < 0\)(1)
Đặt \(\sqrt {{x^2} + 5x + 28} = t\left( {t > 0} \right)\)
(1) trở thành: \({t^2} - 5t - 24 < 0 \Leftrightarrow - 3 < t < 8\)
\(\begin{array}{l} \Rightarrow {x^2} + 5x + 28 < 64\\ \Leftrightarrow {x^2} + 5x - 36 < 0 \Leftrightarrow - 9 < x < 4\end{array}\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2











Danh sách bình luận