Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
Đề bài
Trong các mệnh đề sau mệnh đề nào sai?
-
A.
Dùng nét đứt biểu diễn cho đường bị che khuất
-
B.
Hình biểu diễn của đường thẳng là đường thẳng
-
C.
Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng
-
D.
Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song
Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A,B,C,D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?
-
A.
$4$.
-
B.
$5$.
-
C.
$6$.
-
D.
$8$.
Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ thì $I$ không phải là điểm chung của hai mặt phẳng nào sau đây?
-
A.
$\left( {BCD} \right)$ và $\left( {DEF} \right).$
-
B.
\(\left( {BCD} \right)\) và $\left( {ABC} \right).$
-
C.
\(\left( {BCD} \right)\) và $\left( {AEF} \right).$
-
D.
$\left( {BCD} \right)$ và $\left( {ABD} \right).$
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(AD\) và \(BC.\) Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:
-
A.
\(SD.\)
-
B.
\(SO{\rm{ }}(O\) là tâm hình bình hành \(ABCD).\)
-
C.
\(SG{\rm{ }}(G\) là trung điểm \(AB).\)
-
D.
\(SF{\rm{ }}(F\) là trung điểm \(CD).\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?
-
A.
\(IJCD\) là hình thang
-
B.
\(\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\)
-
C.
\(\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\)
-
D.
\(\left( {IAC} \right) \cap \left( {JBD} \right) = AO{\rm{ }}(O\) là tâm \(ABCD).\)
Cho hai đường thẳng \(a,b\) có một điểm chung duy nhất. Có thể kết luận gì về vị trí tương đối của hai đường thẳng đó?
-
A.
chéo nhau
-
B.
song song
-
C.
trùng nhau
-
D.
cắt nhau
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:
-
A.
$CM$ trong đó $M$ là trung điểm của $BD$
-
B.
$AC$
-
C.
$DB$
-
D.
$CD$
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
-
A.
Hình thang
-
B.
Hình bình hành
-
C.
Hình chữ nhật
-
D.
Tứ diện vì $MN$ và $BD$ chéo nhau
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD,\) \(M\) là trung điểm \(CD,\) \(I\) là điểm ở trên đoạn thẳng \(AG,\) \(BI\) cắt mặt phẳng \(\left( {ACD} \right)\) tại \(J.\) Khẳng định nào sau đây sai?
-
A.
\(AM = \left( {ACD} \right) \cap \left( {ABG} \right).\)
-
B.
\(A,{\rm{ }}J,{\rm{ }}M\) thẳng hàng
-
C.
\(J\) là trung điểm của \(AM.\)
-
D.
\(DJ = \left( {ACD} \right) \cap \left( {BDJ} \right).\)
Hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ cắt nhau theo giao tuyến là đường thẳng $d$. Hai đường thẳng $a,b$ lần lượt nằm trong $\left( \alpha \right),\left( \beta \right)$ và đều cắt đường thẳng $d$. Khẳng định nào sau đây sai?
-
A.
Giao điểm của $a$ và $d$ là giao điểm của $a$ và mặt phẳng $\left( \beta \right)$
-
B.
Giao điểm của $b$ và $d$ là giao điểm của $b$ và mặt phẳng $\left( \alpha \right)$
-
C.
Giao điểm của $b$ và mặt phẳng $\left( \alpha \right)$ nằm ngoài đường thẳng $d$
-
D.
Giao điểm của $a$ và mặt phẳng $\left( \beta \right)$ luôn nằm trên đường thẳng $d$
Cho đường thẳng $d$ và mặt phẳng $\left( \alpha \right)$ . Một mặt phẳng $\left( \beta \right)$ chứa $d$ và cắt $\left( \alpha \right)$ theo giao tuyến là đường thẳng $d'$ . Giao điểm của $d$ và $d'$ là $A$ . Khẳng định nào sau đây là sai?
-
A.
Điểm $A$ thuộc mặt phẳng $\left( \alpha \right)$
-
B.
Điểm $A$ thuộc mặt phẳng $\left( \beta \right)$
-
C.
Điểm $A$ là giao điểm của $d$ và $\left( \alpha \right)$
-
D.
Điểm $A$ là giao điểm của $d'$ và $\left( \beta \right)$
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho \(EF\) cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
-
A.
\(CD,{\rm{ }}EF,{\rm{ }}EG.\)
-
B.
\(CD,{\rm{ }}IG,{\rm{ }}HF.\)
-
C.
\(AB,{\rm{ }}IG,{\rm{ }}HF\).
-
D.
\(AC,{\rm{ }}IG,{\rm{ }}BD.\)
Lời giải và đáp án
Trong các mệnh đề sau mệnh đề nào sai?
-
A.
Dùng nét đứt biểu diễn cho đường bị che khuất
-
B.
Hình biểu diễn của đường thẳng là đường thẳng
-
C.
Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng
-
D.
Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song
Đáp án : D
Hình biểu diễn của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau, không thể là hai đường thẳng song song.
Trong mp\(\left( \alpha \right)\), cho bốn điểm \(A,B,C,D\) trong đó không có ba điểm nào thẳng hàng. Điểm \(S \notin mp\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên?
-
A.
$4$.
-
B.
$5$.
-
C.
$6$.
-
D.
$8$.
Đáp án : C
Sử dụng điều kiện xác định mặt phẳng: Qua ba điểm không thẳng hàng, xác định duy nhất một mặt phẳng.
Điểm \(S\) cùng với hai trong số bốn điểm \(A,B,C,D\) tạo thành một mặt phẳng, từ bốn điểm ta có $6$ cách chọn ra hai điểm, nên có tất cả $6$ mặt phẳng tạo bởi \(S\) và hai trong số bốn điểm nói trên.
Một số em có thể sẽ có lý luận sai như sau: Cứ qua \(3\) điểm ta xác định được \(1\) mặt phẳng nên chọn \(3\) trong số \(5\) điểm có \(C_5^3 = 10\) mặt phẳng là sai.
Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ thì $I$ không phải là điểm chung của hai mặt phẳng nào sau đây?
-
A.
$\left( {BCD} \right)$ và $\left( {DEF} \right).$
-
B.
\(\left( {BCD} \right)\) và $\left( {ABC} \right).$
-
C.
\(\left( {BCD} \right)\) và $\left( {AEF} \right).$
-
D.
$\left( {BCD} \right)$ và $\left( {ABD} \right).$
Đáp án : D
Xác định các đường thẳng $EF,BC$ nằm trong mặt phẳng nào, từ đó suy ra điểm \(I\) nằm trong mặt phẳng nào.
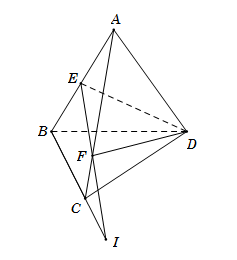
Điểm $I$ là giao điểm của $EF$ và $BC$ mà
\(\left\{ \begin{array}{l}BC \subset \left( {BCD} \right)\\EF \subset \left( {DEF} \right)\\EF \subset \left( {ABC} \right)\\EF \subset \left( {AEF} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I \in \left( {BCD} \right) \cap \left( {DEF} \right)\\I \in \left( {BCD} \right) \cap \left( {ABC} \right)\\I \in \left( {BCD} \right) \cap \left( {AEF} \right)\end{array} \right.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(AD\) và \(BC.\) Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:
-
A.
\(SD.\)
-
B.
\(SO{\rm{ }}(O\) là tâm hình bình hành \(ABCD).\)
-
C.
\(SG{\rm{ }}(G\) là trung điểm \(AB).\)
-
D.
\(SF{\rm{ }}(F\) là trung điểm \(CD).\)
Đáp án : B
- Tìm điểm chung dễ thấy của hai mặt phẳng.
- Tìm điểm chung thứ hai bằng cách tìm hai đường thẳng lần lượt thuộc hai mặt phẳng mà chúng cắt nhau.
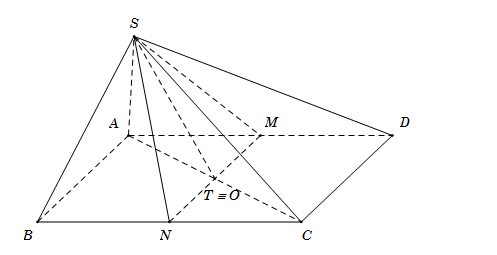
\( \bullet \) \(S\)là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
\( \bullet \) Gọi \(O = AC \cap BD\) là tâm của hình hình hành.
Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(T = AC \cap MN\) $ \Rightarrow T \equiv O$
\( \Rightarrow \left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in MN \subset \left( {SMN} \right) \Rightarrow O \in \left( {SMN} \right)\end{array} \right. \)
\(\Rightarrow O\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
Vậy \(\left( {SMN} \right) \cap \left( {SAC} \right) = SO.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?
-
A.
\(IJCD\) là hình thang
-
B.
\(\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\)
-
C.
\(\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\)
-
D.
\(\left( {IAC} \right) \cap \left( {JBD} \right) = AO{\rm{ }}(O\) là tâm \(ABCD).\)
Đáp án : D
- Xét tính đúng sai của các đáp án bằng cách tìm giao tuyến của mỗi cặp mặt phẳng đã cho ở mỗi đáp án.
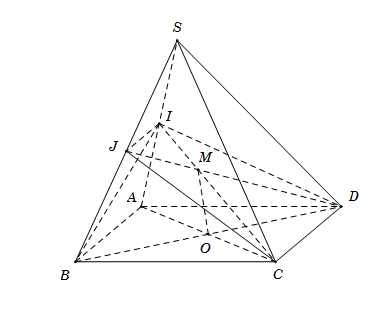
\( \bullet \) Ta có \(IJ\) là đường trung bình của tam giác \(SAB\) \( \Rightarrow IJ\parallel AB\parallel CD \Rightarrow IJ\parallel CD\)
\( \Rightarrow IJCD\) là hình thang. Do đó A đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}IB \subset \left( {SAB} \right)\\IB \subset \left( {IBC} \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( {IBC} \right) = IB.\) Do đó B đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}JD \subset \left( {SBD} \right)\\JD \subset \left( {JBD} \right)\end{array} \right. \Rightarrow \left( {SBD} \right) \cap \left( {JBD} \right) = JD.\) Do đó C đúng.
\( \bullet \) Trong mặt phẳng \(\left( {IJCD} \right)\), gọi \(M = IC \cap JD\)$ \Rightarrow \left( {IAC} \right) \cap \left( {JBD} \right) = MO.$ Do đó D sai.
Cho hai đường thẳng \(a,b\) có một điểm chung duy nhất. Có thể kết luận gì về vị trí tương đối của hai đường thẳng đó?
-
A.
chéo nhau
-
B.
song song
-
C.
trùng nhau
-
D.
cắt nhau
Đáp án : D
Hai đường thẳng có một điểm chung duy nhất thì chúng cắt nhau.
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:
-
A.
$CM$ trong đó $M$ là trung điểm của $BD$
-
B.
$AC$
-
C.
$DB$
-
D.
$CD$
Đáp án : D
Đưa về cùng mặt phẳng và vận dụng các kiến thức hình học phẳng
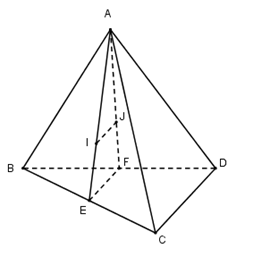
Gọi $E, F$ lần lượt là trung điểm của $BC$ và $BD$ ta có:
$\begin{array}{l}I \in AE\,;\,\dfrac{{AI}}{{AE}} = \dfrac{2}{3}\\J \in AF\,;\,\dfrac{{AJ}}{{AF}} = \dfrac{2}{3}\end{array}$
Xét trong $mp(AEF)$ ta suy ra \(IJ//EF\) (Định lí Ta – let đảo)
Mà $EF$ là đường trung bình của tam giác $ABC$ \( \Rightarrow \) $EF // CD$
Vậy $IJ // CD.$
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
-
A.
Hình thang
-
B.
Hình bình hành
-
C.
Hình chữ nhật
-
D.
Tứ diện vì $MN$ và $BD$ chéo nhau
Đáp án : A
- Sử dụng các tính chất của trọng tâm tam giác.
- Sử dụng tính chất đường trung bình của tam giác.
- Sử dụng định nghĩa hai đường thẳng song song.
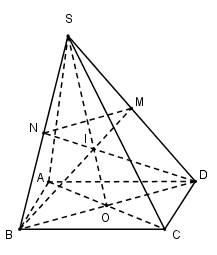
Dễ thấy $I$ là trọng tâm của tam giác $SBD $ nên $BI, DI$ là các đường trung tuyến của tam giác $SBD.$
Suy ra $M, N$ lần lượt là trung điểm của $SD$ và $SB.$
Nên $MN$ là đường trung bình của tam giác $SBD$ \( \Rightarrow \) $MN // BD.$
Vậy tứ giác $MNBD $ là hình thang.
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD,\) \(M\) là trung điểm \(CD,\) \(I\) là điểm ở trên đoạn thẳng \(AG,\) \(BI\) cắt mặt phẳng \(\left( {ACD} \right)\) tại \(J.\) Khẳng định nào sau đây sai?
-
A.
\(AM = \left( {ACD} \right) \cap \left( {ABG} \right).\)
-
B.
\(A,{\rm{ }}J,{\rm{ }}M\) thẳng hàng
-
C.
\(J\) là trung điểm của \(AM.\)
-
D.
\(DJ = \left( {ACD} \right) \cap \left( {BDJ} \right).\)
Đáp án : C
- Xác định giao tuyến của hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\)
- Chứng minh \(J\) thuộc cả hai mặt phẳng \( \Rightarrow J \in AM\).
- Tìm giao tuyến của hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {BDJ} \right)\).
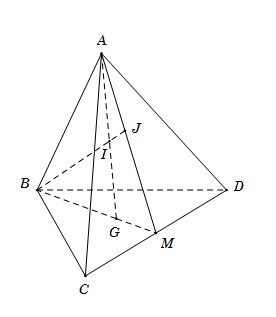
Ta có \(A\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
Do \(BG \cap CD = M \Rightarrow \left\{ \begin{array}{l}M \in BG \subset \left( {ABG} \right) \Rightarrow M \in \left( {ABG} \right)\\M \in CD \subset \left( {ACD} \right) \Rightarrow M \in \left( {ACD} \right)\end{array} \right. \Rightarrow M\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)$\Rightarrow \left( ABG \right)\cap \left( ACD \right)=AM\xrightarrow{{}}$A đúng.
Ta có \(\left\{ \begin{array}{l}BI \subset \left( {ABG} \right)\\AM \subset \left( {ABM} \right)\\\left( {ABG} \right) \equiv \left( {ABM} \right)\end{array} \right. \Rightarrow AM,BI\) đồng phẳng.
\( \Rightarrow J = BI \cap AM \Rightarrow A,J,M\) thẳng hàng$\xrightarrow{{}}$ B đúng.
Ta có $\left\{ \begin{align} & DJ\subset \left( ACD \right) \\ & DJ\subset \left( BDJ \right) \\ \end{align} \right.\Rightarrow DJ=\left( ACD \right)\cap \left( BDJ \right)\xrightarrow{{}}$ D đúng.
Điểm \(I\) di động trên \(AG\) nên \(J\) có thể không phải là trung điểm của \(AM\)
$\xrightarrow{{}}$ C sai
Hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ cắt nhau theo giao tuyến là đường thẳng $d$. Hai đường thẳng $a,b$ lần lượt nằm trong $\left( \alpha \right),\left( \beta \right)$ và đều cắt đường thẳng $d$. Khẳng định nào sau đây sai?
-
A.
Giao điểm của $a$ và $d$ là giao điểm của $a$ và mặt phẳng $\left( \beta \right)$
-
B.
Giao điểm của $b$ và $d$ là giao điểm của $b$ và mặt phẳng $\left( \alpha \right)$
-
C.
Giao điểm của $b$ và mặt phẳng $\left( \alpha \right)$ nằm ngoài đường thẳng $d$
-
D.
Giao điểm của $a$ và mặt phẳng $\left( \beta \right)$ luôn nằm trên đường thẳng $d$
Đáp án : C
Ta tìm giao tuyến của đường thẳng $b$ và mặt phẳng $\left( \alpha \right)$ :
+ Tìm một mặt phẳng chứa $b$ thích hợp
+ Tìm giao tuyến của mặt phẳng này với mặt phẳng $\left( \alpha \right)$
+ Tìm giao điểm của giao tuyến đó với đường thẳng $b$
+ Ta có $\left( \beta \right)$ là mặt phẳng chứa đường thẳng b
+ Giao tuyến của $\left( \beta \right)$ và $\left( \alpha \right)$ là $d$
+ Giao điểm của $d$ và $b$ là $M$
$ \Rightarrow M$ là giao điểm của $b$ và $\left( \alpha \right)$
Vậy $M$ nằm trên đường thẳng $d$
Cho đường thẳng $d$ và mặt phẳng $\left( \alpha \right)$ . Một mặt phẳng $\left( \beta \right)$ chứa $d$ và cắt $\left( \alpha \right)$ theo giao tuyến là đường thẳng $d'$ . Giao điểm của $d$ và $d'$ là $A$ . Khẳng định nào sau đây là sai?
-
A.
Điểm $A$ thuộc mặt phẳng $\left( \alpha \right)$
-
B.
Điểm $A$ thuộc mặt phẳng $\left( \beta \right)$
-
C.
Điểm $A$ là giao điểm của $d$ và $\left( \alpha \right)$
-
D.
Điểm $A$ là giao điểm của $d'$ và $\left( \beta \right)$
Đáp án : D
Ta tìm giao tuyến của đường thẳng $b$ và mặt phẳng $\left( \alpha \right)$ :
+ Tìm một mặt phẳng chứa $b$ thích hợp
+ Tìm giao tuyến của mặt phẳng này với mặt phẳng $\left( \alpha \right)$
+ Tìm giao điểm của giao tuyến đó với đường thẳng $b$
Vì $A \in d'$ mà $d' \subset \left( \alpha \right)$ và $d' \subset \left( \beta \right)$ nên $A \in \left( \alpha \right)$ và \(A \in \left( \beta \right)\)
Vì $A$ là giao điểm của $d$ và $d'$ nên $A \in d$
Mà $A \in \left( \alpha \right)$ nên $A$ là giao điểm của $d$ và $\left( \alpha \right)$
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho \(EF\) cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
-
A.
\(CD,{\rm{ }}EF,{\rm{ }}EG.\)
-
B.
\(CD,{\rm{ }}IG,{\rm{ }}HF.\)
-
C.
\(AB,{\rm{ }}IG,{\rm{ }}HF\).
-
D.
\(AC,{\rm{ }}IG,{\rm{ }}BD.\)
Đáp án : B
Để chứng minh ba đường thẳng \({d_1},{\rm{ }}{d_2},{\rm{ }}{d_3}\) đồng quy ta chứng minh giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\) là điểm chung của hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\); đồng thời \({d_3}\) là giao tuyến \(\left( \alpha \right)\) và \(\left( \beta \right)\).
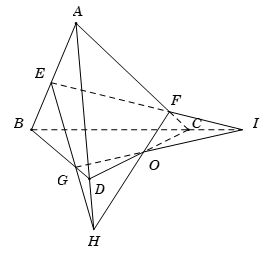
Gọi \(O = HF \cap IG\). Ta có
\(O \in HF\) mà \(HF \subset \left( {ACD} \right)\) suy ra \(O \in \left( {ACD} \right)\).
\(O \in IG\) mà \(IG \subset \left( {BCD} \right)\) suy ra \(O \in \left( {BCD} \right)\).
Do đó \(O \in \left( {ACD} \right) \cap \left( {BCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {ACD} \right) \cap \left( {BCD} \right) = CD\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in CD\).
Vậy ba đường thẳng \(CD,{\rm{ }}IG,{\rm{ }}HF\) đồng quy.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2










Danh sách bình luận