-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút – Chương 1 – Đại số và Giải tích 11
-
Đề kiểm tra 15 phút – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút – Chương 3 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 1 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 2 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 3 - Hình học 11
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết ) - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 11
-
-
Đề thi giữa kì 1
-
Đề thi học kì 1
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi giữa kì 1 Toán 11 - Đề số 2
Đề bài
Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?
-
A.
\(m = - 3\)
-
B.
\(m = - 2\)
-
C.
\(m = 0\)
-
D.
\(m = 3\)
Phương trình \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1\) có nghiệm là:
-
A.
\(x = \dfrac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
-
B.
\(x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
C.
\(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\left( {k \in Z} \right)\)
-
D.
\(x = - \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = 3\sin x + 4\cos x - 1\):
-
A.
\(\min y = - 6;\max y = 4\)
-
B.
\(\min y = - 5;\max y = 5\)
-
C.
\(\min y = - 3;\max y = 4\)
-
D.
\(\min y = - 6;\max y = 6\)
Điền cụm từ thích hợp vào chỗ chấm: “Phép đồng nhất là phép biến hình biến điểm \(M\) thành …”.
-
A.
điểm $M'$ sao cho $MM' = 1$
-
B.
điểm $M'$ sao cho $MM' = 2$
-
C.
điểm $M'$ sao cho $MM' < 1$
-
D.
chính nó
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho $T$ là một phép tịnh tiến theo vectơ $\overrightarrow u $ biến điểm $M\left( {x;y} \right)$ thành điểm $M'\left( {x';y'} \right)$ với biểu thức tọa độ là: $x = x' + 3;\,\,y = y' - 5$. Tọa độ của vectơ tịnh tiến $\overrightarrow u $ là:
-
A.
$\left( {5; - 3} \right)$
-
B.
$\left( {3;5} \right)$
-
C.
$\left( { - 3;5} \right)$
-
D.
\(\left( {3; - 5} \right)\)
Số phát biểu đúng trong các phát biểu sau:
(1) Phép tịnh tiến và phép đối xứng trục đều biến đường thẳng thành đường thẳng song song, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đương tròn thành đường tròn có cùng bán kính.
(2) Tứ giác $ABCD$ là hình thang cân đáy \(AD//BC\). Gọi $M,N$ lần lượt là trung điểm của hai cạnh bên $AB$ và $CD$. Khi đó, đường thẳng $MN$ là trục đối xứng của $ABCD$.
(3) Cho đường thẳng $d$ có phương trình \(y = - x\). Ảnh của đường tròn \(\left( C \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 7\) qua phép đối xứng trục $d$ là \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} = 7\)
(4) Ảnh của đường phân giác ứng với góc phần tư thứ $(I)$ qua phép đối xứng trục $Oy$ là đường thẳng $d$ có phương trình \(y = - x\)
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
-
A.
\(M'\left( { - 1; - 1} \right)\)
-
B.
\(M'\left( {1;1} \right)\)
-
C.
\(M'\left( { - 1;1} \right)\)
-
D.
\(M'\left( {1;0} \right)\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x + 2y - 1 = 0\) và điểm \(I\left( {1;0} \right)\). Phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) có phương trình là:
-
A.
\(x - 2y + 3 = 0.\)
-
B.
\(x + 2y - 1 = 0.\)
-
C.
\(2x - y + 1 = 0.\)
-
D.
\(x + 2y + 3 = 0.\)
Mệnh đề nào sau đây là đúng?
-
A.
Phép đồng dạng tỉ số \(k = 1\) là phép dời hình.
-
B.
Phép đồng dạng tỉ số \(k = - 1\) là phép đối xứng tâm.
-
C.
Phép đồng dạng tỉ số \(k = 1\) là phép tịnh tiến
-
D.
Phép đồng dạng tỉ số \(k = 1\) là phép vị tự tỉ số \(k = 1\)
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\)
-
A.
\(\min y = - \dfrac{2}{3};\max y = 2\)
-
B.
\(\min y = \dfrac{2}{3};\max y = 2\)
-
C.
\(\min y = \dfrac{1}{2};\max y = \dfrac{3}{2}\)
-
D.
\(\min y = - \dfrac{1}{2};\max y = \dfrac{3}{2}\)
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
-
A.
-
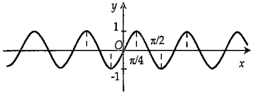
B.
-
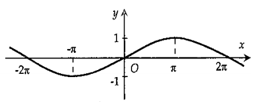
C.
-
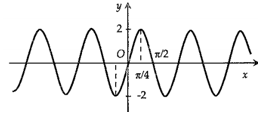
D.
Giải phương trình \(\cot \left( {3x - 1} \right) = - \sqrt 3 .\)
-
A.
$x = \dfrac{1}{3} + \dfrac{{5\pi }}{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
B.
$x = \dfrac{1}{3} + \dfrac{\pi }{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
C.
$x = \dfrac{{5\pi }}{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
D.
$x = \dfrac{1}{3} - \dfrac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).$
Số các giá trị nguyên của \(m\) để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm là:
-
A.
\(4\).
-
B.
\(2\).
-
C.
\(3\).
-
D.
\(5\).
Trong mặt phẳng \(Oxy\), tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\): \({x^2} + {y^2} = 1\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
-
A.
\({x^2} + {\left( {y - 2} \right)^2} = 1\).
-
B.
\({\left( {x + 2} \right)^2} + {y^2} = 1\).
-
C.
\({\left( {x - 2} \right)^2} + {y^2} = 1\).
-
D.
\({x^2} + {\left( {y + 2} \right)^2} = 1\).
Điểm \(O\left( {0;0} \right)\) luôn thuộc đồ thị hàm số
-
A.
\(y = \cos x\)
-
B.
\(y = \sin x\)
-
C.
\(y = \cot x\)
-
D.
\(y = \tan x - 1\)
Tìm m để phương trình $m\sin x + 5\cos x = m + 1$ có nghiệm.
-
A.
$m \le 12$.
-
B.
$m \le 6$
-
C.
$m \le 24$.
-
D.
$m \le 3$.
Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng \(\Delta \) có phương trình \(y = - 3x + 2\). Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ \(\vec u = \left( { - 1;2} \right)\) và \(\vec v = \left( {3;1} \right)\) thì đường thẳng \(\Delta \) biến thành đường thẳng \(d\) có phương trình là:
-
A.
\(y = - 3x + 1.\)
-
B.
\(y = - 3x - 5.\)
-
C.
\(y = - 3x + 9.\)
-
D.
\(y = - 3x + 11.\)
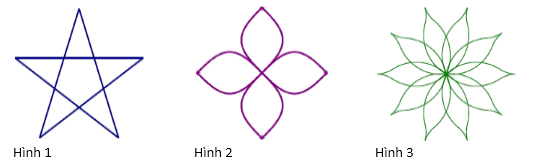
Hình nào sau đây có trục đối xứng và đồng thời có tâm đối xứng?
-
A.
Hình 1 và Hình 2
-
B.
Hình 1 và Hình 3.
-
C.
Hình 2 và Hình 3.
-
D.
Hình 1, Hình 2 và Hình 3.
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\).
-
A.
-
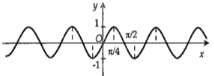
B.
-
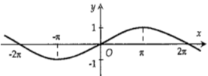
C.
-
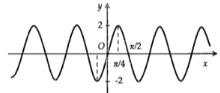
D.
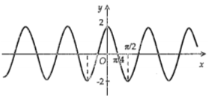
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
-
A.
\(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{10}}\).
-
B.
\(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).
-
C.
\(x = \dfrac{{k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{20}}\).
-
D.
\(x = \dfrac{{k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{10}}\).
Số nghiệm của phương trình \(\tan x = \tan \dfrac{{3\pi }}{{11}}\) trên khoảng \(\left( {\dfrac{\pi }{4};2\pi } \right)\) là:
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Giải phương trình \(\sin 18x\cos 13x = \sin 9x\cos 4x\).
-
A.
\(x = \dfrac{{k\pi }}{18};\,\,x = \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
B.
\(x = \dfrac{{k\pi }}{9};\,\,x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
C.
\(x = \dfrac{\pi }{{3}} + \dfrac{{k\pi }}{18};\,\,x = \dfrac{\pi }{{22}} + \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
D.
\(x = \dfrac{{k\pi }}{3};\,\,x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{44}}\,\,\left( {k \in \mathbb{Z}} \right)\).
Giải phương trình \(2{\sin ^2}2x + \sin 7x - 1 = \sin x\).
-
A.
\(x = - \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{9}\).
-
B.
\(x = \pm \dfrac{\pi }{{18}} + {{k2\pi }}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
-
C.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
-
D.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{18}\), \(x = - \dfrac{{5\pi }}{{18}} + \dfrac{{k\pi }}{3}\).
Cho hình bình hành ABCD. Phép tịnh tiến theo \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\) biến đoạn thẳng DC thành đoạn thẳng nào sau đây?
-
A.
BC
-
B.
AB
-
C.
DC
-
D.
CA
Trong mặt phẳng \(Oxy,\) cho hai đường tròn \(\left( {{C_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 1;\,\)\(\left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 4.\) Tìm tâm vị tự ngoài của hai đường tròn.
-
A.
\(\left( { - 2;3} \right).\)
-
B.
\(\left( {2;3} \right).\)
-
C.
\(\left( {3; - 2} \right).\)
-
D.
\(\left( {1; - 3} \right).\)
Lời giải và đáp án
Với giá trị nào của \(m\) dưới đây thì phương trình \(\sin x = m\) có nghiệm?
-
A.
\(m = - 3\)
-
B.
\(m = - 2\)
-
C.
\(m = 0\)
-
D.
\(m = 3\)
Đáp án : C
Phương trình \(\sin x = m\) có nghiệm nếu \(\left| m \right| \le 1\) và vô nghiệm nếu \(\left| m \right| > 1\)
Đáp án A: $|m|=|-3|=3>1$=> Loại
Đáp án B: $|m|=|-2|=2>1$=> Loại
Đáp án C: $|m|=|0|=0\le 1$ => Nhận
Đáp án D: $|m|=|3|=3>1$=> Loại
Một số em có thể sẽ chọn nhầm đáp án D vì nghĩ \(m > 0\) thì phương trình có nghiệm là sai.
Phương trình \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1\) có nghiệm là:
-
A.
\(x = \dfrac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
-
B.
\(x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
-
C.
\(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\left( {k \in Z} \right)\)
-
D.
\(x = - \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
Đáp án : B
Bước 1: Sử dụng giá trị lượng giác của các góc hơn kém nhau một góc \(\dfrac{\pi }{2}\)
$\tan \left( {\dfrac{\pi }{2} - x} \right) =\cot x$; $\tan \left( {2x + \dfrac{\pi }{2}} \right) =-\cot 2x$
Bước 2: Biến đổi phương trình và giải
+) Công thức nhân đôi \(\cot 2x = \dfrac{{1 - {{\tan }^2}x}}{{2\tan x}}\).
+) Sử dụng công thức $\tan x = \tan y \Leftrightarrow x = y+ k\pi \left( {k \in Z} \right)$
Bước 1:
Ta có: \(\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1 \)\(\Leftrightarrow \cot x - 2\cot 2x = 1\)
ĐK: \(\left\{ \begin{array}{l}\sin x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow x \ne \dfrac{{k\pi }}{2}\)
Bước 2:
Khi đó phương trình tương đương:
\(\begin{array}{l}\cot x - 2\cot 2x = 1 \\ \Leftrightarrow \cot x - 2.\dfrac{{1 - {{\tan }^2}x}}{{2\tan x}} = 1 \\ \Leftrightarrow \cot x - \dfrac{{\tan x.\cot x - {{\tan }^2}x}}{{\tan x}} = 1\\ \Leftrightarrow \cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\left( {TMDK} \right)\end{array}\)
Cần vận dụng linh hoạt các công thức biến đổi lượng giác để áp dụng vào bài toán.
Một số em khi biến đổi \(\cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow - \tan x = 1 \Leftrightarrow \tan x = - 1\) và chọn nhầm đáp án D là sai.
Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = 3\sin x + 4\cos x - 1\):
-
A.
\(\min y = - 6;\max y = 4\)
-
B.
\(\min y = - 5;\max y = 5\)
-
C.
\(\min y = - 3;\max y = 4\)
-
D.
\(\min y = - 6;\max y = 6\)
Đáp án : A
Bước 1: Biến đổi $(y+1)^2$
Bước 2: Sử dụng bất đẳng thức Bu – nhi – a Cốp – xki: \({\left( {ac + bd} \right)^2}\le\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) \).
Bước 3: Xét dấu bằng xảy ra
Dấu "=" xảy ra khi và chỉ khi \(\dfrac{c}{a} = \dfrac{d}{b}\)
Áp dụng công thức $\tan x=a \Leftrightarrow x=\arctan a + k\pi$ để tìm x.
Bước 1:
Ta có: \(y = 3\sin x + 4\cos x - 1 \) \(\Leftrightarrow y + 1 = 3\sin x + 4\cos x\)
\(\Rightarrow{\left( {y + 1} \right)^2}= {\left( {3\sin x + 4\cos x} \right)^2} \)
Bước 2:
Sử dụng bất đẳng thức Bu – nhi – a Cốp – xki: \({\left( {ac + bd} \right)^2}\le\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) \) . Với $a=3, c=\sin x, b=4, d=\cos x$
Khi đó \({\left( {3.\sin x + 4.\cos x} \right)^2} \le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\)\( = \left( {{3^2} + {4^2}} \right).1 = 25 \) \(\Rightarrow - 5 \le y + 1 \le 5 \Leftrightarrow - 6 \le y \le 4\)
Bước 3:
Dấu “=” xảy ra \( \Leftrightarrow \dfrac{{\sin x}}{3} = \dfrac{{\cos x}}{4} \)\(\Leftrightarrow \tan x = \dfrac{3}{4}\) \( \Leftrightarrow x = \arctan \dfrac{3}{4} + k\pi \)
Một số em khi đánh giá được \( - 5 \le y + 1 \le 5\) thì vội vàng chọn đáp án B là sai.
Điền cụm từ thích hợp vào chỗ chấm: “Phép đồng nhất là phép biến hình biến điểm \(M\) thành …”.
-
A.
điểm $M'$ sao cho $MM' = 1$
-
B.
điểm $M'$ sao cho $MM' = 2$
-
C.
điểm $M'$ sao cho $MM' < 1$
-
D.
chính nó
Đáp án : D
Với mỗi điểm \(M\) xác định điểm \(M' \equiv M\). Phép biến hình này là phép đồng nhất.
Một số em có thể sẽ chọn nhầm đáp án A vì hiểu nhầm rằng \(MM' = 1\) nghĩa là \(M \equiv M'\).
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho $T$ là một phép tịnh tiến theo vectơ $\overrightarrow u $ biến điểm $M\left( {x;y} \right)$ thành điểm $M'\left( {x';y'} \right)$ với biểu thức tọa độ là: $x = x' + 3;\,\,y = y' - 5$. Tọa độ của vectơ tịnh tiến $\overrightarrow u $ là:
-
A.
$\left( {5; - 3} \right)$
-
B.
$\left( {3;5} \right)$
-
C.
$\left( { - 3;5} \right)$
-
D.
\(\left( {3; - 5} \right)\)
Đáp án : C
Sử dụng biểu thức tọa độ của phép tịnh tiến \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}x = x' + 3\\y = y' - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 5\end{array} \right. \Rightarrow \overrightarrow u = \left( { - 3;5} \right)\)
Một số em có thể sẽ chọn nhầm đáp án D vì nhớ nhầm biểu thức tọa độ của phép tịnh tiến.
Số phát biểu đúng trong các phát biểu sau:
(1) Phép tịnh tiến và phép đối xứng trục đều biến đường thẳng thành đường thẳng song song, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đương tròn thành đường tròn có cùng bán kính.
(2) Tứ giác $ABCD$ là hình thang cân đáy \(AD//BC\). Gọi $M,N$ lần lượt là trung điểm của hai cạnh bên $AB$ và $CD$. Khi đó, đường thẳng $MN$ là trục đối xứng của $ABCD$.
(3) Cho đường thẳng $d$ có phương trình \(y = - x\). Ảnh của đường tròn \(\left( C \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 7\) qua phép đối xứng trục $d$ là \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} = 7\)
(4) Ảnh của đường phân giác ứng với góc phần tư thứ $(I)$ qua phép đối xứng trục $Oy$ là đường thẳng $d$ có phương trình \(y = - x\)
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : A
Xét tính đúng sai của từng đáp án.
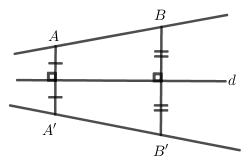
Dựa vào hình vẽ trên ta thấy $2$ đường thẳng đối xứng qua đường thẳng $d$ không song song \( \Rightarrow \) (1) sai.
Xét (2): \(M,N\) là trung điểm của hai cạnh bên \(AB,CD\) nên \(MN\) là đường trung bình của hình thang chứ không phải trục đối xứng. Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy nên (2) sai.
Xét (3): Đường tròn \(\left( C \right)\) có tâm \(I\left( {5;3} \right)\) và bán kính \(R = \sqrt 7 \), đường tròn \(\left( {C'} \right)\) có tâm \(I'\left( {5; - 3} \right)\), bán kính \(R' = \sqrt 7 \)
Gọi $H$ là trung điểm của \(II' \Rightarrow H\left( {5;0} \right) \notin \left( {y = - x} \right) \Rightarrow \left( 3 \right)\) sai.
Xét (4): Đường phân giác ứng với góc phần tư thứ $(I) $ có phương trình \(y = x\) có ảnh qua phép đối xứng trục $Oy$ là đường phân giác của góc phần tư thứ $(II)$ có phương trình \(y = - x \Rightarrow \left( 4 \right)\) đúng.
Vậy chỉ có $1$ phát biểu đúng.
Một số em có thể sẽ nghĩ rằng mệnh đề (2) đúng vì không vẽ hình rồi chọn nhầm đáp án B là sai.
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
-
A.
\(M'\left( { - 1; - 1} \right)\)
-
B.
\(M'\left( {1;1} \right)\)
-
C.
\(M'\left( { - 1;1} \right)\)
-
D.
\(M'\left( {1;0} \right)\)
Đáp án : B
Xác định góc quay.
Áp dụng công thức tính tọa độ ảnh của điểm \(M\left( {x;y} \right)\) qua phép quay tâm $O$ góc \(\alpha :\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
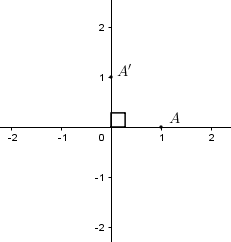
Phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\) là phép quay tâm $O$ góc \({90^0}\)
Gọi \(M'\left( {x';y'} \right)\) là ảnh của điểm \(M\left( {1; - 1} \right)\) qua phép quay tâm $O$ góc \({90^0}\) ta có: \(\left\{ \begin{array}{l}x' = 1.\cos {90^0} + 1.\sin {90^0}\\y' = 1.\sin {90^0} - 1.\cos {90^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 1\\y' = 1\end{array} \right. \Rightarrow M'\left( {1;1} \right)\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x + 2y - 1 = 0\) và điểm \(I\left( {1;0} \right)\). Phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) có phương trình là:
-
A.
\(x - 2y + 3 = 0.\)
-
B.
\(x + 2y - 1 = 0.\)
-
C.
\(2x - y + 1 = 0.\)
-
D.
\(x + 2y + 3 = 0.\)
Đáp án : B
Phép vị tự tâm \(I \in \Delta \) biến đường thẳng \(\Delta \) thành chính nó.
Để ý thấy \(I \in \Delta \) do đó phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) trùng với \(\Delta \), với mọi \(k \ne 0.\)
Mệnh đề nào sau đây là đúng?
-
A.
Phép đồng dạng tỉ số \(k = 1\) là phép dời hình.
-
B.
Phép đồng dạng tỉ số \(k = - 1\) là phép đối xứng tâm.
-
C.
Phép đồng dạng tỉ số \(k = 1\) là phép tịnh tiến
-
D.
Phép đồng dạng tỉ số \(k = 1\) là phép vị tự tỉ số \(k = 1\)
Đáp án : A
Khi \(k = 1\) phép đồng dạng bảo toàn khoảng cách nên là phép dời hình.
Một số em có thể sẽ chọn nhầm đáp án D là sai vì phép đồng dạng tỉ số \(k = 1\) cũng có thể là phép vị tự tỉ số \(k = - 1\).
Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\)
-
A.
\(\min y = - \dfrac{2}{3};\max y = 2\)
-
B.
\(\min y = \dfrac{2}{3};\max y = 2\)
-
C.
\(\min y = \dfrac{1}{2};\max y = \dfrac{3}{2}\)
-
D.
\(\min y = - \dfrac{1}{2};\max y = \dfrac{3}{2}\)
Đáp án : B
Bước 1: Biến đổi hàm số về dạng $a.\sin x+b.\cos x=c$
Bước 2: Sử dụng điều kiện có nghiệm của nó suy ra GTLN, GTNN của hàm số:
$a^2+b^2\ge c^2$
Bước 1:
Ta có \(\cos x + 2 > 0,\forall x \in \,R\) .
\(y = \dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}}\) \( \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3 = 2y + y\cos x\) \( \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{inx}} + \left( {2 - y} \right)\cos x = 2y-3\,\left( * \right)\)
Bước 2:
Ta có điều kiện có nghiệm của phương trình \(\left( * \right)\) là:
\({1^2} + {\left( {2 - y} \right)^2} \ge {\left( {2y-3} \right)^2}\) \( \Leftrightarrow 4{y^2} - 12y + 9 - {y^2} + 4y - 4 - 1 \le 0\) \( \Leftrightarrow 3{y^2} - 8y + 4 \le 0\) \( \Leftrightarrow \dfrac{2}{3} \le y \le 2\)
Ta có thể sử dụng SHIFT SOLVE: \(\dfrac{{{\mathop{\rm s}\nolimits} {\rm{inx}} + 2\cos x + 3}}{{2 + \cos x}} = 2\) thì phương trình có nghiệm.
Do $2$ là số lớn nhất trong các phương án A;B;C;D nên ta không cần thử trường hợp $\max = \dfrac{3}{2}$.
Lúc này chỉ còn A và B. Thử với \(\min y = - \dfrac{2}{3}\) thì không có nghiệm.
Từ đây chọn B.
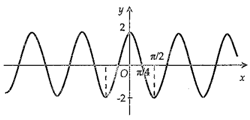
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
-
A.
-
B.
-
C.
-
D.
Đáp án : C
Tìm tập giá trị, chu kì của hàm số \(y = 2\sin 2x\) và điểm đi qua của nó, từ đó đối chiếu đáp án và kết luận.
Ta thấy \( - 2 \le 2\sin 2x \le 2\) nên ta có loại A và B.
Tiếp theo với C và D ta có:
Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kì \(\dfrac{{2\pi }}{{\left| 2 \right|}} = \pi .\)
Ta thấy với \(x = 0\) thì \(y = 0\) nên đồ thị hàm số đi qua gốc tọa độ.
Giải phương trình \(\cot \left( {3x - 1} \right) = - \sqrt 3 .\)
-
A.
$x = \dfrac{1}{3} + \dfrac{{5\pi }}{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
B.
$x = \dfrac{1}{3} + \dfrac{\pi }{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
C.
$x = \dfrac{{5\pi }}{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right).$
-
D.
$x = \dfrac{1}{3} - \dfrac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).$
Đáp án : A
Phương trình \(\cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi ,k \in \mathbb{Z}\)
Ta có $\cot \left( {3x - 1} \right) = - \sqrt 3 \Leftrightarrow \cot \left( {3x - 1} \right) = \cot \left( { - \dfrac{\pi }{6}} \right)$
$ \Leftrightarrow 3x - 1 = - \dfrac{\pi }{6} + k\pi \Leftrightarrow x = \dfrac{1}{3} - \dfrac{\pi }{{18}} + k\dfrac{\pi }{3}{\rm{ }}\left( {k \in \mathbb{Z}} \right)$
Hay $x = \dfrac{1}{3} + \dfrac{{5\pi }}{{18}} + \dfrac{{l\pi }}{3},l \in \mathbb{Z}$
Số các giá trị nguyên của \(m\) để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm là:
-
A.
\(4\).
-
B.
\(2\).
-
C.
\(3\).
-
D.
\(5\).
Đáp án : A
- Đặt \(t = \sqrt {\cos + m} \) đưa phương trình về hệ phương trình
- Sử dụng phương pháp cộng đại số biến đổi hệ phương trình đưa về phương trình dạng tích.
- Tìm điều kiện để phương trình có nghiệm, sử dụng kiến thức của hàm số bậc hai.
Ta có: \({\cos ^2}x + \sqrt {\cos x + m} = m\) suy ra \(m \ge 0\).
Đặt \(\sqrt {\cos x + m} = t\), \(t \ge 0\). Phương trình trở thành: $\left\{ \begin{array}{l}{\cos ^2}x + t = m\\{t^2} - \cos x = m\end{array} \right.$
$ \Rightarrow \,\left( {{{\cos }^2}x - {t^2}} \right) + \left( {t + \cos x} \right) = 0$$ \Leftrightarrow \left( {\cos x + t} \right)\left( {\cos x - t + 1} \right) = 0$$ \Leftrightarrow \left[ \begin{array}{l}\cos x = - t\\\cos x - t + 1 = 0\end{array} \right.$
+) Trường hợp \(1\): \(\cos x = - t\) \( \Rightarrow \sqrt {\cos x + m} = - \cos x\) \( \Leftrightarrow \left\{ \begin{array}{l}\cos x \le 0\\{\cos ^2}x - \cos x = m\end{array} \right.\)
Đặt \(u = \cos x\)\(\left( { - 1 \le u \le 0} \right)\)
Xét hàm số \(f\left( u \right) = {u^2} - u\) trên đoạn \(\left[ { - 1;0} \right]\), có hoành độ đỉnh \(x = \dfrac{1}{2} \notin \left[ { - 1;0} \right]\) và bảng biến thiên:
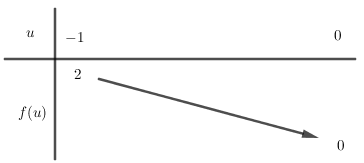
Để phương trình có nghiệm thì \(m \in \left[ {0;\,2} \right]\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {0;\,1;\,2} \right\}\).
+) Trường hợp \(2\): \(\cos x - t + 1 = 0\)\( \Leftrightarrow \sqrt {\cos x + m} = 1 + \cos x\)\( \Leftrightarrow {\cos ^2}x + \,\cos x + 1 = m\).
Đặt $v = \cos x$, $ - 1 \le v \le 1$. Ta có \(m = {v^2} + v + 1 = g\left( v \right)\)
Hàm số bậc hai \(g\left( v \right)\) có hoành độ đỉnh \(v = - \dfrac{1}{2} \in \left[ { - 1;1} \right]\) có bảng biến thiên :
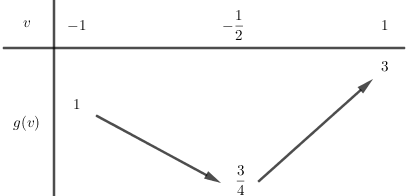
Để phương trình có nghiệm thì \(m \in \left[ {\dfrac{3}{4};3} \right]\).
Vì \(m \in \mathbb{Z}\) nên \(m \in \left\{ {1;\,2;\,3} \right\}\).
Vậy có tất cả \(4\) số nguyên \(m\) thỏa mãn bài toán.
Trong mặt phẳng \(Oxy\), tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\): \({x^2} + {y^2} = 1\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
-
A.
\({x^2} + {\left( {y - 2} \right)^2} = 1\).
-
B.
\({\left( {x + 2} \right)^2} + {y^2} = 1\).
-
C.
\({\left( {x - 2} \right)^2} + {y^2} = 1\).
-
D.
\({x^2} + {\left( {y + 2} \right)^2} = 1\).
Đáp án : C
Tìm tâm và bán kính đường tròn mới qua phép đối xứng tâm \(I\left( {1;0} \right)\)
Đường tròn \(\left( C \right)\) có tâm \(O\left( {0;\;0} \right)\), bán kính \(R = 1\).
Gọi \(O'\) là ảnh của \(O\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
Ta có: $\left\{ {\begin{array}{*{20}{c}}{\dfrac{{{x_O} + {x_{O'}}}}{2} = {x_I}}\\{\dfrac{{{y_O} + {y_{O'}}}}{2} = {y_I}}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{O'}} = 2{x_I} - {x_O}}\\{{y_{O'}} = 2{y_I} - {y_O}}\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_{O'}} = 2.1 - 0}\\{{y_{O'}} = 2.0 - 0}\end{array}} \right.$$ \Rightarrow O'\left( {2;\;0} \right)$.
Đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\) qua phép đối xứng tâm \(I\left( {1;\;0} \right)\).
\(\left( {C'} \right)\) có tâm $O'\left( {2;\;0} \right)$, bán kính \(R' = R = 1\).
Phương trình đường tròn \(\left( {C'} \right)\) là: \({\left( {x - 2} \right)^2} + {y^2} = 1\).
Điểm \(O\left( {0;0} \right)\) luôn thuộc đồ thị hàm số
-
A.
\(y = \cos x\)
-
B.
\(y = \sin x\)
-
C.
\(y = \cot x\)
-
D.
\(y = \tan x - 1\)
Đáp án : B
Thay tọa độ điểm \(O\) vào tủng hàm số và kiểm tra.
Đáp án A sai vì \(\cos 0 = 1\).
Đáp án B đúng vì \(\sin 0 = 0\).
Đáp án C sai vì \(\cot 0\) không xác định.
Đáp án D sai vì \(\tan 0 - 1 = - 1 \ne 0\).
Tìm m để phương trình $m\sin x + 5\cos x = m + 1$ có nghiệm.
-
A.
$m \le 12$.
-
B.
$m \le 6$
-
C.
$m \le 24$.
-
D.
$m \le 3$.
Đáp án : A
Điều kiện để phương trình \(a\cos x + b\sin x = c\) có nghiệm là \({a^2} + {b^2} \ge {c^2}\)
Phương trình có nghiệm $ \Leftrightarrow {m^2} + 25 \ge {\left( {m + 1} \right)^2} \Leftrightarrow 2m \le 24 \Leftrightarrow m \le 12$.
Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng \(\Delta \) có phương trình \(y = - 3x + 2\). Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ \(\vec u = \left( { - 1;2} \right)\) và \(\vec v = \left( {3;1} \right)\) thì đường thẳng \(\Delta \) biến thành đường thẳng \(d\) có phương trình là:
-
A.
\(y = - 3x + 1.\)
-
B.
\(y = - 3x - 5.\)
-
C.
\(y = - 3x + 9.\)
-
D.
\(y = - 3x + 11.\)
Đáp án : D
- Tìm véc tơ tịnh tiến.
- Sử dụng biểu thức tọa độ của phép tịnh tiến $\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' - a\\y = y' - b\end{array} \right.$
Từ giả thiết suy ra \(d\) là ảnh của \(\Delta \) qua phép tịnh tiến theo vectơ \(\vec a = \vec u + \vec v\).
Ta có \(\vec a = \vec u + \vec v = \left( {2;3} \right)\).
Biểu thức tọa độ của phép \({T_{\overrightarrow a }}\) là \(\left\{ \begin{array}{l}x = x' - 2\\y = y' - 3\end{array} \right.\) thay vào \(\Delta \) ta được$y' - 3 = - 3\left( {x' - 2} \right) + 2$
$ \Leftrightarrow \,y' = - 3x' + 11$.
Hình nào sau đây có trục đối xứng và đồng thời có tâm đối xứng?
-
A.
Hình 1 và Hình 2
-
B.
Hình 1 và Hình 3.
-
C.
Hình 2 và Hình 3.
-
D.
Hình 1, Hình 2 và Hình 3.
Đáp án : C
Quan sát hình vẽ và nhận xét trục và tâm đối xứng của mỗi hình.
Hình 1: chỉ có trục đối xứng (\(5\) đường thẳng) và không có tâm đối xứng.
Hình 2: Có \(4\) trục đối xứng và có \(1\) tâm đối xứng.
Hình 3: Có \(10\) trục đối xứng và có \(1\) tâm đối xứng.
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\).
-
A.
-
B.
-
C.
-
D.
Đáp án : C
- Dựa vào tập giá trị của hàm sin.
- Dựa vào điểm đi qua của đồ thị hàm số.
Ta có: \( - 2 \le 2\sin 2x \le 2\) nên loại đáp án A và B.
Cho \(x = 0 \Rightarrow y = 2\sin 0 = 0\), do đó đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\) đi qua điểm (0;0). Loại đáp án D.
Phương trình \(\cos 11x\cos 3x = \cos 17x\cos 9x\) có nghiệm là:
-
A.
\(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{10}}\).
-
B.
\(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).
-
C.
\(x = \dfrac{{k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{20}}\).
-
D.
\(x = \dfrac{{k\pi }}{3},\,\,x = \dfrac{{k\pi }}{{10}}\).
Đáp án : B
Bước 1: Sử dụng công thức biến đổi tích thành tổng: \(\cos a\cos b = \dfrac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\) để đưa về phương trình lượng giác cơ bản.
Bước 2: Giải phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Bước 1:
$\cos 11x\cos 3x = \cos 17x\cos 9x$
\( \Leftrightarrow \dfrac{1}{2}.\left[ {\cos \left( {11x + 3x} \right) + \cos \left( {11x - 3x} \right)} \right]\)\( = \dfrac{1}{2}\left[ {\cos \left( {17x + 9x} \right) + \cos \left( {17x - 9x} \right)} \right]\)
$\Leftrightarrow \dfrac{1}{2}\left( {\cos 14x + \cos 8x} \right) = \dfrac{1}{2}\left( {\cos 26x + \cos 8x} \right)\\ \Leftrightarrow \cos 14x + \cos 8x = \cos 26x + \cos 8x\\ \Leftrightarrow \cos 14x = \cos 26x$
Bước 2:
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}26x = 14x + k2\pi \\26x = - 14x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}12x = k2\pi \\40x = k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{6}\\x = \dfrac{{k\pi }}{{20}}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy nghiệm của phương trình là \(x = \dfrac{{k\pi }}{6},\,\,x = \dfrac{{k\pi }}{{20}}\).
Số nghiệm của phương trình \(\tan x = \tan \dfrac{{3\pi }}{{11}}\) trên khoảng \(\left( {\dfrac{\pi }{4};2\pi } \right)\) là:
-
A.
1
-
B.
2
-
C.
3
-
D.
4
Đáp án : B
- Giải phương trình lượng giác cơ bản: \[\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\].
- Cho nghiệm tìm được thuộc khoảng \(\left( {\dfrac{\pi }{4};2\pi } \right)\), tìm các giá trị k nguyên thỏa mãn, từ đó suy ra số nghiệm của phương trình thỏa mãn yêu cầu bài toán.
Ta có: \(\tan x = \tan \dfrac{{3\pi }}{{11}} \Leftrightarrow x = \dfrac{{3\pi }}{{11}} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Theo bài ra ta có:
\(\begin{array}{l}x \in \left( {\dfrac{\pi }{4};2\pi } \right)\\ \Rightarrow \dfrac{\pi }{4} < \dfrac{{3\pi }}{{11}} + k\pi < 2\pi \\ \Leftrightarrow - \dfrac{\pi }{{44}} < k\pi < \dfrac{{19\pi }}{{11}}\\ \Leftrightarrow - \dfrac{1}{{44}} < k < \dfrac{{19}}{{11}}\end{array}\)
Mà \(k \in \mathbb{Z}\) \( \Rightarrow k \in \left\{ {0;1} \right\}\).
Vậy phương trình đã cho có 2 nghiệm thỏa mãn yêu cầu bài toán.
Giải phương trình \(\sin 18x\cos 13x = \sin 9x\cos 4x\).
-
A.
\(x = \dfrac{{k\pi }}{18};\,\,x = \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
B.
\(x = \dfrac{{k\pi }}{9};\,\,x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
C.
\(x = \dfrac{\pi }{{3}} + \dfrac{{k\pi }}{18};\,\,x = \dfrac{\pi }{{22}} + \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\).
-
D.
\(x = \dfrac{{k\pi }}{3};\,\,x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{44}}\,\,\left( {k \in \mathbb{Z}} \right)\).
Đáp án : B
- Sử dụng công thức biến đổi tích thành tổng: \(\sin a\cos b = \dfrac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\).
- Giải phương trình lượng giác cơ bản: \(sinx = sin\alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
\(\begin{array}{l}\,\,\,\,\,\sin 18x\cos 13x = \sin 9x\cos 4x\\ \Leftrightarrow \dfrac{1}{2}\left( {\sin 31x + \sin 5x} \right) = \dfrac{1}{2}\left( {\sin 13x + \sin 5x} \right)\\ \Leftrightarrow \sin 31x + \sin 5x = \sin 13x + \sin 5x\\ \Leftrightarrow \sin 31x = \sin 13x\\ \Leftrightarrow \left[ \begin{array}{l}31x = 13x + k2\pi \\31x = \pi - 13x + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}18x = k2\pi \\44x = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{k\pi }}{9}\\x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{22}}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy nghiệm của phương trình là \(x = \dfrac{{k\pi }}{9};\,\,x = \dfrac{\pi }{{44}} + \dfrac{{k\pi }}{{22}}\,\,\left( {k \in \mathbb{Z}} \right)\)
Giải phương trình \(2{\sin ^2}2x + \sin 7x - 1 = \sin x\).
-
A.
\(x = - \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{9}\).
-
B.
\(x = \pm \dfrac{\pi }{{18}} + {{k2\pi }}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
-
C.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
-
D.
\(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k\pi }}{18}\), \(x = - \dfrac{{5\pi }}{{18}} + \dfrac{{k\pi }}{3}\).
Đáp án : C
- Nhóm \(2{\sin ^2}2x - 1\), \(\sin 7x - \sin x\).
- Sử dụng công thức nhân đôi: \(\cos 2\alpha = 1 - 2{\sin ^2}\alpha \), công thức biến đổi tổng thành tích: \(\sin a - \sin b = 2\cos \dfrac{{a + b}}{2}\sin \dfrac{{a - b}}{2}\).
- Đưa phương trình đã cho về dạng tích.
- Giải phương trình lượng giác cơ bản: \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
\(\begin{array}{l}\,\,\,\,\,\,2{\sin ^2}2x + \sin 7x - 1 = \sin x\\ \Leftrightarrow \left( {2{{\sin }^2}2x - 1} \right) + \sin 7x - \sin x = 0\\ \Leftrightarrow - \cos 4x + 2\cos 4x\sin 3x = 0\\ \Leftrightarrow \cos 4x\left( {2\sin 3x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\cos 4x = 0\\\sin 3x = \dfrac{1}{2}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}4x = \dfrac{\pi }{2} + k\pi \\3x = \dfrac{\pi }{6} + k2\pi \\3x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\\x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là: \(x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\), \(x = \dfrac{\pi }{{18}} + \dfrac{{k2\pi }}{3}\), \(x = \dfrac{{5\pi }}{{18}} + \dfrac{{k2\pi }}{3}\).
Cho hình bình hành ABCD. Phép tịnh tiến theo \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\) biến đoạn thẳng DC thành đoạn thẳng nào sau đây?
-
A.
BC
-
B.
AB
-
C.
DC
-
D.
CA
Đáp án : B
Sử dụng định nghĩa phép tịnh tiến: \({T_{\overrightarrow u }}\left( A \right) = B \Rightarrow \overrightarrow {AB} = \overrightarrow u \).
Ta có: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \).
Mà ABCD là hình bình hành nên \(\overrightarrow {CB} = \overrightarrow {DA} \).
Do đó
\(\begin{array}{l}{T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( D \right) = {T_{\overrightarrow {CB} }}\left( D \right) = A\\{T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( C \right) = {T_{\overrightarrow {CB} }}\left( C \right) = B\end{array}\)
Vậy \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( {DC} \right) = {T_{\overrightarrow {CB} }}\left( {DC} \right) = AB\)
Trong mặt phẳng \(Oxy,\) cho hai đường tròn \(\left( {{C_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 1;\,\)\(\left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 4.\) Tìm tâm vị tự ngoài của hai đường tròn.
-
A.
\(\left( { - 2;3} \right).\)
-
B.
\(\left( {2;3} \right).\)
-
C.
\(\left( {3; - 2} \right).\)
-
D.
\(\left( {1; - 3} \right).\)
Đáp án : A
\(\left( {{C_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 1\) \( \Rightarrow \) tâm \({I_1}\left( {3; - 1} \right)\), bán kinh \({R_1} = 1\)
\(\left( {{C_2}} \right):{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 4\)\( \Rightarrow \) tâm \({I_2}\left( {4;3} \right)\), bán kinh \({R_2} = 2\)
Gọi \(I\) là tâm vị tự của 2 đường tròn với \(I\left( {x;y} \right)\)
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {I\,{I_1}} \left( {1 - x;3 - y} \right)\\\overrightarrow {I\,{I_2}} \left( {4 - x;3 - y} \right)\end{array} \right.\)
\(k = \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{1}{2}\) (\(k > 0\) vì đây là vị tự ngoài)
\(\begin{array}{l} \Rightarrow \overrightarrow {I\,{I_1}} = \dfrac{1}{2}\overrightarrow {I\,{I_2}} \\ \Leftrightarrow \left\{ \begin{array}{l}1 - x = \dfrac{1}{2}\left( {4 - x} \right)\\3 - y = \dfrac{1}{2}\left( {3 - y} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 3\end{array} \right.\end{array}\)
Vậy vị tự tâm ngoài \(\left( { - 2;3} \right)\).
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2
