-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút – Chương 1 – Đại số và Giải tích 11
-
Đề kiểm tra 15 phút – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút – Chương 3 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 1 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 2 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 3 - Hình học 11
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết ) - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 11
-
-
Đề thi giữa kì 1
-
Đề thi học kì 1
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi giữa kì 1 Toán 11 - Đề số 3
Đề bài
Cho phương trình \(\sin x = \sin \alpha \). Chọn kết luận đúng.
-
A.
\(\left[ \begin{array}{l}x = \alpha + k\pi \\x = \pi - \alpha + k\pi \end{array} \right.\left( {k \in Z} \right)\)
-
B.
\(\left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
-
C.
\(\left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
-
D.
\(\left[ \begin{array}{l}x = \alpha + k\pi \\x = - \alpha + k\pi \end{array} \right.\left( {k \in Z} \right)\)
Số nghiệm của phương trình \(2\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = 0\) với \(\pi \le x \le 5\pi \) là:
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(3\)
-
D.
\(2\)
Hàm số nào sau đây có đồ thị không là đường hình sin?
-
A.
\(y = \sin x\)
-
B.
\(y = \cos x\)
-
C.
\(y = \sin 2x\)
-
D.
\(y = \cot x\)
Tìm tập xác định của hàm số \(y = \tan \left( {2x - \dfrac{\pi }{4}} \right)\).
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{8} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{8} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{8} + k\pi ,k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{4} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
Phép tịnh tiến theo véc tơ \(\overrightarrow u \) biến điểm \(M\) thành \(M'\) và điểm \(N\) thành \(N'\) thì:
-
A.
\(\overrightarrow {MM'} = \overrightarrow {NN'} \)
-
B.
\(\overrightarrow {MM'} = \overrightarrow {N'N} \)
-
C.
\(\overrightarrow {MN'} = \overrightarrow {NM'} \)
-
D.
\(\overrightarrow {MN} = \overrightarrow u \)
Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
-
A.
Không có
-
B.
Một
-
C.
Hai
-
D.
Vô số
Phép quay tâm $O$ góc \( - {90^0}\) biến đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x + 1 = 0\) thành đường tròn có phương trình:
-
A.
\({x^2} + {\left( {y - 2} \right)^2} = 3\)
-
B.
\({x^2} + {\left( {y + 2} \right)^2} = 9\)
-
C.
\({x^2} + {\left( {y + 2} \right)^2} = 5\)
-
D.
\({x^2} + {\left( {y + 2} \right)^2} = 3\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x + 2y - 1 = 0\) và điểm \(I\left( {1;0} \right)\). Phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) có phương trình là:
-
A.
\(x - 2y + 3 = 0.\)
-
B.
\(x + 2y - 1 = 0.\)
-
C.
\(2x - y + 1 = 0.\)
-
D.
\(x + 2y + 3 = 0.\)
Phép vị tự nào sau đây biến đường tròn \(\left( C \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) thành đường tròn \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 4\) ?
-
A.
\({V_{\left( {I; - 1} \right)}}\) với \(I\left( {4;2} \right)\)
-
B.
\(V\left( {I;1} \right)\) với \(I\left( {1;1} \right)\)
-
C.
\({V_{\left( {I; - 1} \right)}}\) với \(I\left( {1;1} \right)\)
-
D.
\({V_{\left( {I;1} \right)}}\) với \(I\left( {4;2} \right)\)
Cho \(\Delta ABC\) và \(\Delta A'B'C'\) đồng dạng với nhau theo tỉ số \(k\). Chọn câu sai:
-
A.
\(k\) là tỉ số hai trung tuyến tương ứng
-
B.
\(k\) là tỉ số hai đường cao tương ứng
-
C.
\(k\) là tỉ số hai góc tương ứng
-
D.
\(k\) là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng
Tập xác định của hàm số \(y = \dfrac{1}{{2\cos x - 1}}\) là:
-
A.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k2\pi ,\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
B.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
C.
${\rm{D}} = \left\{ {\dfrac{\pi }{3} + k2\pi ,\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
D.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016.\)
-
A.
$\min y = 1;\max y = 4033.$
-
B.
\(\min y = - 1;\max y = 4033.\)
-
C.
\(\min y = 1;\max y = 4022.\)
-
D.
\(\min y = - 1;\max y = 4022.\)
Gọi \({x_0}\) là nghiệm dương nhỏ nhất của phương trình \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0\). Mệnh đề nào sau đây là đúng?
-
A.
\({x_0} \in \left( {0;\dfrac{\pi }{4}} \right).\)
-
B.
\({x_0} \in \left[ {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right].\)
-
C.
\({x_0} \in \left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{4}} \right).\)
-
D.
\({x_0} \in \left[ {\dfrac{{3\pi }}{4};\pi } \right].\)
Khẳng định nào sau đây là đúng về phương trình \(\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) + \cos \left( {\dfrac{\pi }{2} + \dfrac{{80}}{{{x^2} + 32x + 332}}} \right) = 0\)?
-
A.
Số nghiệm của phương trình là \(8\).
-
B.
Tổng các nghiệm của phương trình là \(8\).
-
C.
Tổng các nghiệm của phương trình là \(48\).
-
D.
Phương trình có vô số nghiệm thuộc \(\mathbb{R}\).
Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng \(d:\)\(3x - y + 2 = 0\). Viết phương trình đường thẳng \(d'\) là ảnh của $d$ qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\).
-
A.
\(d':x + 3y + 2 = 0\).
-
B.
\(d':x + 3y - 2 = 0\).
-
C.
\(d':3x - y - 6 = 0\).
-
D.
\(d':x - 3y - 2 = 0\).
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\):
-
A.
\(\max y = 6;\min y = - 2\)
-
B.
\(\max y = 4;\min y = - 4\)
-
C.
\(\max y = 6;\min y = - 4\)
-
D.
\(\max y = 6;\min y = - 1\)
Phương trình $\tan x + \tan \left( {x + \dfrac{\pi }{3}} \right) + \tan \left( {x + \dfrac{{2\pi }}{3}} \right) = 3\sqrt 3 $ tương đương với phương trình.
-
A.
$\cot x = \sqrt 3 $.
-
B.
$\cot 3x = \sqrt 3 $.
-
C.
$\tan x = \sqrt 3 $.
-
D.
$\tan 3x = \sqrt 3 $.
Giải phương trình \({\sin ^2}x + {\sin ^2}x{\tan ^2}x = 3\).
-
A.
\(x = \pm \dfrac{\pi }{6} + k\pi \).
-
B.
\(x = \pm \dfrac{\pi }{6} + k2\pi \).
-
C.
\(x = \pm \dfrac{\pi }{3} + k\pi \).
-
D.
\(x = \pm \dfrac{\pi }{3} + k2\pi \).
Tìm m để phương trình $m\sin x + 5\cos x = m + 1$ có nghiệm.
-
A.
$m \le 12$.
-
B.
$m \le 6$
-
C.
$m \le 24$.
-
D.
$m \le 3$.
Phương trình \(\sqrt 3 \cos 3x + \sin 3x = \sqrt 2 \) có nghiệm là:
-
A.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
B.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + \dfrac{{k\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
C.
\(\left[ \begin{array}{l}x = \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = - \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
D.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + k2\pi \\x = \dfrac{{5\pi }}{{36}} + k2\pi \,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A\left( {2;5} \right).\) Phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {1;2} \right)\) biến \(A\) thành điểm \(A'\) có tọa độ là:
-
A.
\(A'\left( {3;1} \right).\)
-
B.
\(A'\left( {1;6} \right).\)
-
C.
\(A'\left( {3;7} \right).\)
-
D.
\(A'\left( {4;7} \right).\)
Trong mặt phẳng tọa độ $Oxy$, phép đối xứng trục biến điểm $A\left( {2;1} \right)$ thành $A'\left( {2;5} \right)$ có trục đối xứng là:
-
A.
Đường thẳng \(y = 3.\)
-
B.
Đường thẳng \(x = 3.\)
-
C.
Đường thẳng \(y = 6.\)
-
D.
Đường thẳng \(x + y - 3 = 0.\)
Phương trình lượng giác \(\dfrac{{\cos x - \dfrac{{\sqrt 3 }}{2}}}{{\sin x - \dfrac{1}{2}}} = 0\) có nghiệm là:
-
A.
\(x = \dfrac{\pi }{6} + k2\pi \)
-
B.
Vô nghiệm
-
C.
\(x = - \dfrac{\pi }{6} + k2\pi \)
-
D.
\(x = \pm \dfrac{\pi }{6} + k2\pi \)
Phương trình \(\sin \left( {2x + \dfrac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi:
-
A.
\( - 1 < m < 0\)
-
B.
\( - 3 < m < - 1\)
-
C.
\(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l}m < - 2\\m > 0\end{array} \right.\)
Trong mặt phẳng tọa độ \(Oxy\), cho \(\Delta :\,\,x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là:
-
A.
\(x - 2y + 1 = 0\)
-
B.
\(x - 2y + 9 = 0\)
-
C.
\(x - 2y - 3 = 0\)
-
D.
\(x - 2y - 9 = 0\)
Lời giải và đáp án
Cho phương trình \(\sin x = \sin \alpha \). Chọn kết luận đúng.
-
A.
\(\left[ \begin{array}{l}x = \alpha + k\pi \\x = \pi - \alpha + k\pi \end{array} \right.\left( {k \in Z} \right)\)
-
B.
\(\left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
-
C.
\(\left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
-
D.
\(\left[ \begin{array}{l}x = \alpha + k\pi \\x = - \alpha + k\pi \end{array} \right.\left( {k \in Z} \right)\)
Đáp án : B
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
Một số em có thể sẽ chọn nhầm đáp án A vì không để ý \(k2\pi \).
Số nghiệm của phương trình \(2\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = 0\) với \(\pi \le x \le 5\pi \) là:
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(3\)
-
D.
\(2\)
Đáp án : D
Biến đổi phương trình về dạng \(\sin x = m\) rồi sử dụng phương trình lượng giác cơ bản \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\)
Ta có:
\(2\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = 0 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = 1 \Leftrightarrow x + \dfrac{\pi }{4} = \dfrac{\pi }{2} + k2\pi \Leftrightarrow x = \dfrac{\pi }{4} + k2\pi \left( {k \in Z} \right)\)
Mà \(\pi \le x \le 5\pi \Rightarrow \pi \le \dfrac{\pi }{4} + k2\pi \le 5\pi \Leftrightarrow \dfrac{{3\pi }}{4} \le k2\pi \le \dfrac{{19\pi }}{4} \Leftrightarrow \dfrac{3}{8} \le k \le \dfrac{{19}}{8} \Rightarrow k \in \left\{ {1;2} \right\}\)
Vậy phương trình có hai nghiệm trong đoạn \(\left[ {\pi ;5\pi } \right]\).
Một số em có thể sẽ chọn nhầm đáp án C vì xác định sai các giá trị của \(k\) khi thay vào điều kiện đề bài.
Hàm số nào sau đây có đồ thị không là đường hình sin?
-
A.
\(y = \sin x\)
-
B.
\(y = \cos x\)
-
C.
\(y = \sin 2x\)
-
D.
\(y = \cot x\)
Đáp án : D
Các hàm số sin, cos đều có đồ thị là đường hình sin nên các đáp án A, B, C đều có đồ thị là đường hình sin.
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng hàm số \(y = \cos x\) không có đồ thị là đường hình sin là sai.
Tìm tập xác định của hàm số \(y = \tan \left( {2x - \dfrac{\pi }{4}} \right)\).
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{8} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{8} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{8} + k\pi ,k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{3\pi }}{4} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
Đáp án : B
Hàm số \(y = \tan u\left( x \right)\) xác định nếu \(\cos u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne \dfrac{\pi }{2} + k\pi \).
Điều kiện: \(\cos \left( {2x - \dfrac{\pi }{4}} \right) \ne 0 \Leftrightarrow 2x - \dfrac{\pi }{4} \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow 2x \ne \dfrac{{3\pi }}{4} + k\pi \Leftrightarrow x \ne \dfrac{{3\pi }}{8} + \dfrac{k\pi }{2}\)
Một số em có thể sẽ nhầm thành \(\cos u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne k\pi \) và chọn nhầm đáp án A là sai.
Một số khác lại nhớ nhầm điều kiện \(\cos u\left( x \right) \ne 0 \Leftrightarrow u\left( x \right) \ne \dfrac{\pi }{2} + k2\pi \) và chọn nhầm đáp án C là sai.
Phép tịnh tiến theo véc tơ \(\overrightarrow u \) biến điểm \(M\) thành \(M'\) và điểm \(N\) thành \(N'\) thì:
-
A.
\(\overrightarrow {MM'} = \overrightarrow {NN'} \)
-
B.
\(\overrightarrow {MM'} = \overrightarrow {N'N} \)
-
C.
\(\overrightarrow {MN'} = \overrightarrow {NM'} \)
-
D.
\(\overrightarrow {MN} = \overrightarrow u \)
Đáp án : A
Sử dụng định nghĩa phép tịnh tiến:
Cho véc tơ \(\overrightarrow u \), với mỗi điểm \(M\) ta xác định điểm \(M'\) thỏa mãn \(\overrightarrow {MM'} = \overrightarrow u \). Phép biến hình này là phép tịnh tiến theo véc tơ \(\overrightarrow u \).
Phép tịnh tiến theo véc tơ \(\overrightarrow u \) biến điểm \(M\) thành \(M'\) thì \(\overrightarrow {MM'} = \overrightarrow u \).
Phép tịnh tiến theo véc tơ \(\overrightarrow u \) biến điểm \(N\) thành \(N'\) thì \(\overrightarrow {NN'} = \overrightarrow u \).
Do đó \(\overrightarrow {MM'} = \overrightarrow {NN'} \).
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng \(\overrightarrow {MM'} = \overrightarrow u = \overrightarrow {N'N} \) là sai.
Hình gồm hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng?
-
A.
Không có
-
B.
Một
-
C.
Hai
-
D.
Vô số
Đáp án : B
Vẽ hình và tìm tâm đối xứng.
Hình gồm hai đường tròn phân biệt có cùng bán kính có tâm đối xứng duy nhất là trung điểm có đoạn thẳng nối tâm hai đường tròn đó
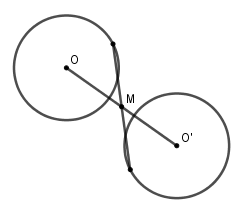
Phép quay tâm $O$ góc \( - {90^0}\) biến đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x + 1 = 0\) thành đường tròn có phương trình:
-
A.
\({x^2} + {\left( {y - 2} \right)^2} = 3\)
-
B.
\({x^2} + {\left( {y + 2} \right)^2} = 9\)
-
C.
\({x^2} + {\left( {y + 2} \right)^2} = 5\)
-
D.
\({x^2} + {\left( {y + 2} \right)^2} = 3\)
Đáp án : D
Đường tròn \(\left( {I;R} \right)\) qua phép quay tâm O góc quay \(\alpha \) biến thành đường tròn \(\left( {I';R'} \right)\) sao cho \(\left\{ \begin{array}{l}{Q_{\left( {O;\alpha } \right)}}\left( I \right) = I'\\R' = R\end{array} \right.\)
Đường tròn $\left( C \right)$ có tâm \(I\left( {2;0} \right)\) , bán kính \(R = \sqrt {{2^2} + {0^2} - 1} = \sqrt 3 \)
\({Q_{\left( {O; - {{90}^0}} \right)}}\left( I \right) = I'\left( {0; - 2} \right) \Rightarrow {Q_{\left( {O; - {{90}^0}} \right)}}:\,\,\left( C \right)\,\, \mapsto \,\,\left( {C'} \right)\) có tâm \(I'\left( {0; - 2} \right)\) và bán kính \(R' = R = \sqrt 3 \)
Vậy phương trình đường tròn \(\left( {C'} \right)\) là: \({\left( {x - 0} \right)^2} + {\left( {y + 2} \right)^2} = 3 \Leftrightarrow {x^2} + {\left( {y + 2} \right)^2} = 3\)
Trong mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x + 2y - 1 = 0\) và điểm \(I\left( {1;0} \right)\). Phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) có phương trình là:
-
A.
\(x - 2y + 3 = 0.\)
-
B.
\(x + 2y - 1 = 0.\)
-
C.
\(2x - y + 1 = 0.\)
-
D.
\(x + 2y + 3 = 0.\)
Đáp án : B
Phép vị tự tâm \(I \in \Delta \) biến đường thẳng \(\Delta \) thành chính nó.
Để ý thấy \(I \in \Delta \) do đó phép vị tự tâm \(I\) tỉ số \(k\) biến đường thẳng \(\Delta \) thành \(\Delta '\) trùng với \(\Delta \), với mọi \(k \ne 0.\)
Phép vị tự nào sau đây biến đường tròn \(\left( C \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} = 4\) thành đường tròn \(\left( {C'} \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 3} \right)^2} = 4\) ?
-
A.
\({V_{\left( {I; - 1} \right)}}\) với \(I\left( {4;2} \right)\)
-
B.
\(V\left( {I;1} \right)\) với \(I\left( {1;1} \right)\)
-
C.
\({V_{\left( {I; - 1} \right)}}\) với \(I\left( {1;1} \right)\)
-
D.
\({V_{\left( {I;1} \right)}}\) với \(I\left( {4;2} \right)\)
Đáp án : A
Gọi phép vị tự cần tìm là \({V_{\left( {I;k} \right)}}\), có \(\left| k \right| = \dfrac{{R'}}{R}\)
Gọi $K$ và $K'$ lần lượt là tâm của đường tròn \(\left( C \right)\) và đường tròn \(\left( {C'} \right)\) ta có \(\overrightarrow {IK'} = k\overrightarrow {IK} \)
Đường tròn \(\left( C \right)\) có tâm \(K\left( {3;1} \right)\) và bán kính \(R = 2\), đường tròn \(\left( {C'} \right)\) có tâm \(K'\left( {5;3} \right)\) và bán kính \(R' = 2\).
\( \Rightarrow \left| k \right| = \dfrac{{R'}}{R} = 1 \Rightarrow k = \pm 1\), mà \(I' \ne I \Rightarrow k \ne 1 \Rightarrow k = - 1\)
Giả sử phép vị tự tâm $I$ tỉ số $k$ biến $K$ thành $K'$ ta có: \(\overrightarrow {IK'} = - \overrightarrow {IK} \Rightarrow I\) là trung điểm của \(KK' \Rightarrow I\left( {4;2} \right)\)
Cho \(\Delta ABC\) và \(\Delta A'B'C'\) đồng dạng với nhau theo tỉ số \(k\). Chọn câu sai:
-
A.
\(k\) là tỉ số hai trung tuyến tương ứng
-
B.
\(k\) là tỉ số hai đường cao tương ứng
-
C.
\(k\) là tỉ số hai góc tương ứng
-
D.
\(k\) là tỉ số hai bán kính đường tròn ngoại tiếp tương ứng
Đáp án : C
- Sử dụng tính chất của phép đồng dạng: biến các đường cao, trung tuyến, đường tròn ngoại tiếp, nội tiếp tam giác thành các đường cao, trung tuyến, đường tròn ngoại tiếp, nội tiếp tam giác có cùng tỉ số đồng dạng.
- Phép đồng dạng giữ nguyên độ lớn của góc.
Hai tam giác đồng dạng thì các góc tương ứng bằng nhau nên \(k\) không thể là tỉ số hai góc tương ứng.
Tập xác định của hàm số \(y = \dfrac{1}{{2\cos x - 1}}\) là:
-
A.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k2\pi ,\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
B.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
C.
${\rm{D}} = \left\{ {\dfrac{\pi }{3} + k2\pi ,\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
-
D.
${\rm{D}} = \mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{3} + k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}$
Đáp án : A
Hàm số \(y = \dfrac{1}{{f\left( x \right)}}\) xác định nếu \(f\left( x \right)\) xác định và \(f\left( x \right) \ne 0\)
Hàm số đã cho xác định khi:
\(2\cos x - 1 \ne 0 \Leftrightarrow \cos x \ne \dfrac{1}{2}\)\( \Leftrightarrow x \ne \pm \dfrac{\pi }{3} + k2\pi \) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{3} + k2\pi \\x \ne - \dfrac{\pi }{3} + k2\pi \end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\\x \ne \dfrac{{5\pi }}{3} + l2\pi ,l \in \mathbb{Z}\end{array} \right.\)
Cách khác: Sử dụng máy tính cầm tay tính giá trị của hàm số \(y = \dfrac{1}{{2\cos x - 1}}\) tại \(x = \dfrac{\pi }{3}\) và \(x = \dfrac{{5\pi }}{3}\) ta thấy hàm số đều không xác định, từ đây ta chọn A
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số: \(y = 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016.\)
-
A.
$\min y = 1;\max y = 4033.$
-
B.
\(\min y = - 1;\max y = 4033.\)
-
C.
\(\min y = 1;\max y = 4022.\)
-
D.
\(\min y = - 1;\max y = 4022.\)
Đáp án : B
Ta có các bước để giải quyết bài toán như sau:
Bước 1: Chỉ ra \(f\left( x \right) \le M,\forall x \in D.\)
Bước 2 : Chỉ ra \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\) .
Kết luận : \(\mathop {\max }\limits_D f\left( x \right) = M\)
Tương tự với tìm giá trị nhỏ nhất của hàm số.
Hàm số xác định trên \(R\) .
Ta có \( - 1 \le \cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) \le 1,\forall x \in R.\)
\( \Leftrightarrow - 2017 \le 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) \le 2017,\forall x \in \,R\)
\( \Leftrightarrow - 1 \le 2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016 \le 4033,\forall x \in \,R\)
Ta có \(y = - 1\) khi \(\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) = - 1\) ; \(y = 4033\) khi \(\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) = 1\)
Vậy \(\min y = - 1;\max y = 4033\)
Cách khác: Sử dụng máy tính cầm tay.
Trong bốn phương án chỉ có hai giá trị \(\max \)là \(4022;4033\) .
Chỉ có hai giá trị min là $1; - 1$ .
Lúc này ta sử dụng chức năng SHIFT SOLVE để thử giá trị:
Ví dụ ta nhập vào màn hình $2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016 = 4033$ ta thấy phương trình có nghiệm.
Tương tự nhập $2017\cos \left( {8x + \dfrac{{10\pi }}{{2017}}} \right) + 2016 = - 1$ ta thấy phương trình có nghiệm.
Từ đây ta chọn B.
Gọi \({x_0}\) là nghiệm dương nhỏ nhất của phương trình \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0\). Mệnh đề nào sau đây là đúng?
-
A.
\({x_0} \in \left( {0;\dfrac{\pi }{4}} \right).\)
-
B.
\({x_0} \in \left[ {\dfrac{\pi }{4};\dfrac{\pi }{2}} \right].\)
-
C.
\({x_0} \in \left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{4}} \right).\)
-
D.
\({x_0} \in \left[ {\dfrac{{3\pi }}{4};\pi } \right].\)
Đáp án : D
- Tìm ĐKXĐ.
- Giải phương trình, kết hợp điều kiện và kết luận nghiệm.
Điều kiện: \(1 - \sin 2x \ne 0 \Leftrightarrow \sin 2x \ne 1.\)
Phương trình \(\dfrac{{2\cos 2x}}{{1 - \sin 2x}} = 0 \Leftrightarrow \cos 2x = 0 \Rightarrow \left[ \begin{array}{l}\sin 2x = 1\left( L \right)\\\sin 2x = - 1\left( {TM} \right)\end{array} \right.\)
\( \Leftrightarrow \sin 2x = - 1 \Leftrightarrow 2x = - \dfrac{\pi }{2} + k2\pi \Leftrightarrow x = - \dfrac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\)
Cho \( - \dfrac{\pi }{4} + k\pi > 0 \Rightarrow k > \dfrac{1}{4}\).
Do đó nghiệm dương nhỏ nhất ứng với \(k = 1 \to x = \dfrac{{3\pi }}{4} \in \left[ {\dfrac{{3\pi }}{4};\pi } \right].\)
Khẳng định nào sau đây là đúng về phương trình \(\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) + \cos \left( {\dfrac{\pi }{2} + \dfrac{{80}}{{{x^2} + 32x + 332}}} \right) = 0\)?
-
A.
Số nghiệm của phương trình là \(8\).
-
B.
Tổng các nghiệm của phương trình là \(8\).
-
C.
Tổng các nghiệm của phương trình là \(48\).
-
D.
Phương trình có vô số nghiệm thuộc \(\mathbb{R}\).
Đáp án : C
- Biến đổi phương trình về dạng $\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.$
- Đánh giá giá trị của hai hàm số \(f\left( x \right) = \dfrac{x}{{{x^2} + 6}}\) và \(g\left( x \right) = \dfrac{{80}}{{{x^2} + 32x + 332}}\) trên \(\mathbb{R}\) rồi suy ra nghiệm của phương trình đã cho.
Phương trình đã cho tương đương với \(\sin \left( {\dfrac{x}{{{x^2} + 6}}} \right) = \sin \left( {\dfrac{{80}}{{{x^2} + 32x + 332}}} \right)\quad \left( * \right)\).
Ta biết rằng hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\). Ta chỉ ra rằng các hàm số \(f\left( x \right) = \dfrac{x}{{{x^2} + 6}}\) và \(g\left( x \right) = \dfrac{{80}}{{{x^2} + 32x + 332}}\) nhận giá trị trong khoảng này.
Thật vậy, ta có \(\left| {\dfrac{x}{{{x^2} + 6}}} \right| \le \left| {\dfrac{x}{{2\sqrt {6{x^2}} }}} \right| = \dfrac{1}{{2\sqrt 6 }}\)
và \(0 < \dfrac{{80}}{{{x^2} + 32x + 332}} = \dfrac{{80}}{{{{\left( {x + 16} \right)}^2} + 76}} \le \dfrac{{80}}{{76}} < \dfrac{\pi }{2}\)
Từ các đánh giá trên, \(\left( * \right)\) xảy ra khi và chỉ khi
\(\dfrac{x}{{{x^2} + 6}} = \dfrac{{80}}{{{x^2} + 32x + 332}}\) \( \Leftrightarrow {x^3} - 48{x^2} + 332x - 480 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 6\\x = 40\end{array} \right.\).
Tổng các nghiệm của phương trình đã cho là \(2 + 6 + 40 = 48\).
Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng \(d:\)\(3x - y + 2 = 0\). Viết phương trình đường thẳng \(d'\) là ảnh của $d$ qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\).
-
A.
\(d':x + 3y + 2 = 0\).
-
B.
\(d':x + 3y - 2 = 0\).
-
C.
\(d':3x - y - 6 = 0\).
-
D.
\(d':x - 3y - 2 = 0\).
Đáp án : B
Tìm ảnh của một điểm thuộc \(d\) qua phép quay tâm \(O\) góc quay \( - {90^0}\) và viết phương trình đường thẳng mới với chú ý đường thẳng này vuông góc với đường thẳng đã cho.
Qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\) đường thẳng $d$ biến thành đường thẳng \(d'\) vuông góc với $d$.
Phương trình đường thẳng \(d'\) có dạng: \(x + 3y + m = 0\).
Lấy \(A\left( {0;2} \right) \in d\). Qua phép quay tâm $O$ góc quay \( - {90^{\rm{o}}}\), điểm \(A\left( {0;2} \right)\) biến thành điểm \(B\left( {2;0} \right) \in d'\). Khi đó \(m = - 2\).
Vậy phương trình đường \(d'\) là \(x + 3y - 2 = 0\).
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 3\sin x + 4\cos x + 1\):
-
A.
\(\max y = 6;\min y = - 2\)
-
B.
\(\max y = 4;\min y = - 4\)
-
C.
\(\max y = 6;\min y = - 4\)
-
D.
\(\max y = 6;\min y = - 1\)
Đáp án : C
Sử dụng bất đẳng thức Bu – nhi – a Cốp – xki: \(\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right) \ge {\left( {ac + bd} \right)^2}\)
\(y = 3\sin x + 4\cos x + 1 \Leftrightarrow y - 1 \)\(= 3\sin x + 4\cos x\)
\({\left( {y - 1} \right)^2} = {\left( {3\sin x + 4\cos x} \right)^2}\)
Ta coi \(a = 3;b = 4;c = \sin x;d = \cos x\)
Theo BĐT Bu-nhi-a Cốp-xki ta được:
\({\left( {3.\sin x + 4.\cos x} \right)^2}\)\( \le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2} + {{\cos }^2}x} \right) = 25.1\)
\( \Rightarrow {\left( {y - 1} \right)^2} \le 25 \Leftrightarrow - 5 \le y - 1 \le 5\)
\( \Leftrightarrow - 5 + 1 \le y \le 5 + 1 \Leftrightarrow - 4 \le y \le 6\)
Vậy \(\max y = 6;\min y = - 4\)
Phương trình $\tan x + \tan \left( {x + \dfrac{\pi }{3}} \right) + \tan \left( {x + \dfrac{{2\pi }}{3}} \right) = 3\sqrt 3 $ tương đương với phương trình.
-
A.
$\cot x = \sqrt 3 $.
-
B.
$\cot 3x = \sqrt 3 $.
-
C.
$\tan x = \sqrt 3 $.
-
D.
$\tan 3x = \sqrt 3 $.
Đáp án : D
- Biến đổi phương trình về dạng phương trình lượng giác cơ bản.
- Đối chiếu các đáp án và kết luận nghiệm.
Công thức sử dụng:
$\begin{array}{l}
\tan x=\dfrac{\sin x}{\cos x}\\\tan a + \tan b = \dfrac{{\sin \left( {a + b} \right)}}{{\cos a\cos b}}\\\sin x\cos y + \sin y\cos x = \sin \left( {x + y} \right)\\\sin a\cos b = \dfrac{1}{2}\left( {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right)\\
\cos a\sin b = \dfrac{1}{2}\left( {\sin \left( {a + b} \right) - \sin \left( {a - b} \right)} \right)
\end{array}$
\(\sin \left( {x + \pi } \right) = - \sin x\)
Điều kiện: $\left\{ \begin{array}{l}\cos x \ne 0\\\cos \left( {x + \dfrac{\pi }{3}} \right) \ne 0\\\cos \left( {x + \dfrac{{2\pi }}{3}} \right) \ne 0\end{array} \right.$
${\rm{pt}}$\( \Leftrightarrow \tan x + \tan \left( {x + \dfrac{\pi }{3}} \right) + \tan \left( {x + \dfrac{{2\pi }}{3}} \right)\)\( = 3\sqrt 3 \)
\( \Leftrightarrow \dfrac{{\sin x}}{{\cos x}}\)\( + \left[ {\dfrac{{\sin \left( {x + \dfrac{\pi }{3}} \right)}}{{\cos \left( {x + \dfrac{\pi }{3}} \right)}} + \dfrac{{\sin \left( {x + \dfrac{{2\pi }}{3}} \right)}}{{\cos \left( {x + \dfrac{{2\pi }}{3}} \right)}}} \right] = 3\sqrt 3 \)
\( \Leftrightarrow \dfrac{{\sin x}}{{\cos x}}\)\( + \dfrac{{\sin \left( {x + \dfrac{\pi }{3}} \right).\cos \left( {x + \dfrac{{2\pi }}{3}} \right) + \cos \left( {x + \dfrac{\pi }{3}} \right).\sin \left( {x + \dfrac{{2\pi }}{3}} \right)}}{{\cos \left( {x + \dfrac{\pi }{3}} \right)\cos \left( {x + \dfrac{{2\pi }}{3}} \right)}}\)\( = 3\sqrt 3 \)
\( \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} + \dfrac{{\sin \left[ {\left( {x + \dfrac{\pi }{3}} \right) + \left( {x + \dfrac{{2\pi }}{3}} \right)} \right]}}{{\cos \left( {x + \dfrac{\pi }{3}} \right).\cos \left( {x + \dfrac{{2\pi }}{3}} \right)}} = 3\sqrt 3 {\rm{ }}\)
$ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} + \dfrac{{\sin \left( {2x + \pi } \right)}}{{\cos \left( {x + \dfrac{\pi }{3}} \right)\cos \left( {x + \dfrac{{2\pi }}{3}} \right)}}$$ = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} - \dfrac{{\sin 2x}}{{\dfrac{1}{2}\left[ {\cos \left( {x + \dfrac{{2\pi }}{3} + x + \dfrac{\pi }{3}} \right) + \cos \left( {x + \dfrac{{2\pi }}{3} - x - \dfrac{\pi }{3}} \right)} \right]}} $$= 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} - \dfrac{{2\sin 2x}}{{\cos \left( {2x + \pi } \right) + \cos \left( {\dfrac{\pi }{3}} \right)}} = 3\sqrt 3 $
$\begin{array}{l}
\Leftrightarrow \dfrac{{\sin x}}{{\cos x}} - \dfrac{{2\sin 2x}}{{ - \cos 2x + \dfrac{1}{2}}} = 3\sqrt 3 \\
\Leftrightarrow \dfrac{{\sin x}}{{\cos x}} - \dfrac{{2.2\sin 2x}}{{ - 2\cos 2x + 2.\dfrac{1}{2}}} = 3\sqrt 3
\end{array}$
$ \Leftrightarrow \dfrac{{\sin x}}{{\cos x}} - \dfrac{{4\sin 2x}}{{1 - 2\cos 2x}} = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x\left( {1 - 2\cos 2x} \right) - 4\sin 2x.\cos x}}{{\cos x\left( {1 - 2\cos 2x} \right)}} = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x - 2\sin x\cos 2x - 4\sin 2x\cos x}}{{\cos x\left( {1 - 2\cos 2x} \right)}} = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x - 2.\dfrac{1}{2}\left( {\sin 3x - \sin x} \right) - 4.\dfrac{1}{2}\left( {\sin 3x + \sin x} \right)}}{{\cos x\left( {1 - 2\cos 2x} \right)}} = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{\sin x - \sin 3x + \sin x - 2\sin 3x - 2\sin x}}{{\cos x - \cos x - \cos 3x}} = 3\sqrt 3 $
$ \Leftrightarrow \dfrac{{ - 3\sin 3x}}{{ - \cos 3x}} = 3\sqrt 3 $
$ \Leftrightarrow 3\tan 3x = 3\sqrt 3 \Leftrightarrow \tan 3x = \sqrt 3 $
\( \Leftrightarrow 3x = \dfrac{\pi }{3} + k\pi \Leftrightarrow x = \dfrac{\pi }{9} + \dfrac{{k\pi }}{3}\).
Kiểm tra ta thấy nghiệm \(x = \dfrac{\pi }{9} + \dfrac{{k\pi }}{3}\) thỏa mãn các điều kiện của phương trình đầu.
Do đó phương trình \(\tan 3x = \sqrt 3 \) tương đương với phương trình ban đầu (có cùng tập nghiệm).
Sử dụng các công thức biến đổi lượng giác cơ bản.
Giải phương trình \({\sin ^2}x + {\sin ^2}x{\tan ^2}x = 3\).
-
A.
\(x = \pm \dfrac{\pi }{6} + k\pi \).
-
B.
\(x = \pm \dfrac{\pi }{6} + k2\pi \).
-
C.
\(x = \pm \dfrac{\pi }{3} + k\pi \).
-
D.
\(x = \pm \dfrac{\pi }{3} + k2\pi \).
Đáp án : C
- Tìm ĐKXĐ.
- Biến đổi phương trình về phương trình lượng giác cơ bản.
- Giải phương trình, kiểm tra điều kiện và kết luận nghiệm.
- Sử dụng các công thức:
\(\tan x = \dfrac{{\sin x}}{{\cos x}}\)
\({\sin ^2}x + {\cos ^2}x = 1\)s
ĐK: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \).
\(\begin{array}{l}{\sin ^2}x + {\sin ^2}x{\tan ^2}x = 3\\ \Leftrightarrow {\sin ^2}x\left( {1 + {{\tan }^2}x} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {1 + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {\dfrac{{{{\cos }^2}x}}{{{{\cos }^2}x}} + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x\left( {\dfrac{{{{\cos }^2}x + {{\sin }^2}x}}{{{{\cos }^2}x}}} \right) = 3\\ \Leftrightarrow {\sin ^2}x.\dfrac{1}{{{{\cos }^2}x}} = 3\\ \Leftrightarrow {\tan ^2}x = 3\end{array}\)
\( \Leftrightarrow \left[ \begin{array}{l}\tan x = \sqrt 3 \\\tan x = - \sqrt 3 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\tan x = \tan \dfrac{\pi }{3}\\\tan x = \tan \left( { - \dfrac{\pi }{3}} \right)\end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{3} + k\pi \\x = - \dfrac{\pi }{3} + k\pi \end{array} \right.\)
Tìm m để phương trình $m\sin x + 5\cos x = m + 1$ có nghiệm.
-
A.
$m \le 12$.
-
B.
$m \le 6$
-
C.
$m \le 24$.
-
D.
$m \le 3$.
Đáp án : A
Điều kiện để phương trình \(a\cos x + b\sin x = c\) có nghiệm là \({a^2} + {b^2} \ge {c^2}\)
Phương trình có nghiệm $ \Leftrightarrow {m^2} + 25 \ge {\left( {m + 1} \right)^2} \Leftrightarrow 2m \le 24 \Leftrightarrow m \le 12$.
Phương trình \(\sqrt 3 \cos 3x + \sin 3x = \sqrt 2 \) có nghiệm là:
-
A.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
B.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + \dfrac{{k\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
C.
\(\left[ \begin{array}{l}x = \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = - \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
-
D.
\(\left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + k2\pi \\x = \dfrac{{5\pi }}{{36}} + k2\pi \,\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\)
Đáp án : A
Chia cả hai vế cho \(2\) đưa về phương trình lượng giác cơ bản.
\(\begin{array}{l}\,\,\,\,\,\,\sqrt 3 \cos 3x + \sin 3x = \sqrt 2 \\ \Leftrightarrow \dfrac{{\sqrt 3 }}{2}\cos 3x + \dfrac{1}{2}\sin 3x = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin 3x.\cos \dfrac{\pi }{3} + \cos 3x.\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {3x + \dfrac{\pi }{3}} \right) = \sin \left( {\dfrac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\3x + \dfrac{\pi }{3} = \dfrac{{3\pi }}{4} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3x = - \dfrac{\pi }{{12}} + k2\pi \\3x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \dfrac{\pi }{{36}} + \dfrac{{k2\pi }}{3}\\x = \dfrac{{5\pi }}{{36}} + \dfrac{{k2\pi }}{3}\end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A\left( {2;5} \right).\) Phép tịnh tiến theo vectơ \(\overrightarrow v = \left( {1;2} \right)\) biến \(A\) thành điểm \(A'\) có tọa độ là:
-
A.
\(A'\left( {3;1} \right).\)
-
B.
\(A'\left( {1;6} \right).\)
-
C.
\(A'\left( {3;7} \right).\)
-
D.
\(A'\left( {4;7} \right).\)
Đáp án : C
Bước 1: Gọi \(A'\left( {x;y} \right) \) và biểu diễn $\overrightarrow {AA'}$ theo $x,y$
Bước 2:
Sử dụng biểu thức tọa độ của phép tịnh tiến \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\).
Bước 1:
Gọi \(A'\left( {x;y} \right) \Rightarrow \overrightarrow {AA'} = \left( {x - 2;y - 5} \right).\)
Bước 2:
Ta có \({T_{\overrightarrow v }}\left( A \right) = A' \Leftrightarrow \overrightarrow {AA'} = \overrightarrow v \) \( \Rightarrow \left\{ \begin{array}{l}x - 2 = 1\\y - 5 = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 7\end{array} \right.\)
Trong mặt phẳng tọa độ $Oxy$, phép đối xứng trục biến điểm $A\left( {2;1} \right)$ thành $A'\left( {2;5} \right)$ có trục đối xứng là:
-
A.
Đường thẳng \(y = 3.\)
-
B.
Đường thẳng \(x = 3.\)
-
C.
Đường thẳng \(y = 6.\)
-
D.
Đường thẳng \(x + y - 3 = 0.\)
Đáp án : A
Phép đối xứng trục \({D_d}\) biến điểm \(A\) thành \(A'\) thì \(d\) là đường trung trực của \(AA'\).
Gọi ${D_a}\left( A \right) = A'$ $ \Rightarrow a$ là đường trung trực của đoạn thẳng $AA'.$
Gọi $H$ là trung điểm đoạn thẳng $AA' \Rightarrow H\left( {2;3} \right).$
Ta có $\overrightarrow {AA'} = \left( {0;4} \right) = 4.\left( {0;1} \right).$
Đường thẳng $a$ qua điểm $H$ và có một VTPT $\vec n = \overrightarrow {AA'} = \left( {0;4} \right)$ nên có phương trình $a:y = 3.$
Phương trình lượng giác \(\dfrac{{\cos x - \dfrac{{\sqrt 3 }}{2}}}{{\sin x - \dfrac{1}{2}}} = 0\) có nghiệm là:
-
A.
\(x = \dfrac{\pi }{6} + k2\pi \)
-
B.
Vô nghiệm
-
C.
\(x = - \dfrac{\pi }{6} + k2\pi \)
-
D.
\(x = \pm \dfrac{\pi }{6} + k2\pi \)
Đáp án : C
- Tìm ĐKXĐ của phương trình.
- Giải phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
- Đối chiếu nghiệm và loại nghiệm.
ĐKXĐ: \(\sin x - \dfrac{1}{2} \ne 0 \Rightarrow \sin x \ne \dfrac{1}{2} \Leftrightarrow \left[ \begin{array}{l}x \ne \dfrac{\pi }{6} + k2\pi \\x \ne \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
\(\dfrac{{\cos x - \dfrac{{\sqrt 3 }}{2}}}{{\sin x - \dfrac{1}{2}}} = 0 \Leftrightarrow \cos x - \dfrac{{\sqrt 3 }}{2} = 0 \Leftrightarrow \cos x = \dfrac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = - \dfrac{\pi }{6} + k2\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
Đối chiếu ĐKXĐ ta thấy chỉ có nghiệm \(x = - \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) thỏa mãn.
Vậy nghiệm của phương trình là \(x =- \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Đối với những bài toán có ĐKXĐ, trước khi làm bài ta cần tìm được ĐKXĐ của bài toán. Sau đó phải đối chiếu lại những nghiệm tìm được để loại nghiệm.
Phương trình \(\sin \left( {2x + \dfrac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi:
-
A.
\( - 1 < m < 0\)
-
B.
\( - 3 < m < - 1\)
-
C.
\(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l}m < - 2\\m > 0\end{array} \right.\)
Đáp án : C
Phương trình \(\sin x = m\) vô nghiệm khi và chỉ khi \(\left[ \begin{array}{l}m > 1\\m < - 1\end{array} \right.\).
Phương trình \(\sin \left( {2x + \dfrac{\pi }{7}} \right) = {m^2} - 3m + 3\) vô nghiệm khi và chỉ khi:
\(\left[ \begin{array}{l}{m^2} - 3m + 3 > 1\\{m^2} - 3m + 3 < - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{m^2} - 3m + 2 > 0\\{m^2} - 3m + 4 < 0\,\,\left( {vo\,\,nghiem} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\).
Trong mặt phẳng tọa độ \(Oxy\), cho \(\Delta :\,\,x - 2y - 1 = 0\) và \(\overrightarrow u \left( {4;3} \right)\). Gọi \(d\) là đường thẳng sao cho \({T_{\overrightarrow u }}\) biến \(d\) thành đường thẳng \(\Delta \). Phương trình đường thẳng \(d\) là:
-
A.
\(x - 2y + 1 = 0\)
-
B.
\(x - 2y + 9 = 0\)
-
C.
\(x - 2y - 3 = 0\)
-
D.
\(x - 2y - 9 = 0\)
Đáp án : A
Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó.
Vì \(\Delta = {T_{\overrightarrow u }}\left( d \right) \Rightarrow \Delta \parallel d \Rightarrow \) Phương trình \(\Delta \) có dạng: \(x - 2y + c = 0\,\,\left( \Delta \right)\).
Lấy \(A\left( {1;0} \right)\) bất kì thuộc \(d\). Gọi \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow A' \in \Delta \).
Ta có: \(A' = {T_{\overrightarrow u }}\left( A \right) \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = {x_A} + {x_{\overrightarrow u }} = 1 + 4 = 5\\{y_{A'}} = {y_A} + {y_{\overrightarrow u }} = 0 + 3 = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\).
Vì \(A' \in \Delta \Rightarrow 5 - 2.3 + c = 0 \Leftrightarrow c = 1\).
Vậy phương trình đường thẳng \(\Delta \) là: \(x - 2y + 1 = 0\).
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2
