Đề thi giữa kì 1 Toán 11 - Đề số 4
Đề bài
Số các hoán vị khác nhau của \(n\) phần tử là:
-
A.
\({P_n} = n!\)
-
B.
\({P_n} = n\)
-
C.
\({P_n} = \left( {n - 1} \right)!\)
-
D.
\({P_n} = {n^2}\)
Để phương trình \(\dfrac{{{a^2}}}{{1 - {{\tan }^2}x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\) có nghiệm, tham số a phải thỏa mãn điều kiện:
-
A.
\(\left| a \right| \ge 1\)
-
B.
\(\left| a \right| > 1\)
-
C.
\(\left| a \right| = 1\)
-
D.
\(\left| a \right| \ne 1\)
Với giá trị của $x$ thỏa mãn \(12C_x^1 + C_{x + 4}^2 = 162\) thì \(A_{x - 1}^2 - C_x^1 = ?\)
-
A.
$20$
-
B.
$30$
-
C.
$ - 10$
-
D.
$34$
Công việc \(A\) có \(k\) công đoạn \({A_1},{A_2},...,{A_k}\) với số cách thực hiện lần lượt là \({n_1},{n_2},...,{n_k}\). Khi đó số cách thực hiện công việc \(A\) là:
-
A.
\({n_1} + {n_2} + ... + {n_k}\) cách
-
B.
\({n_1}.{n_2}.....{n_k}\) cách
-
C.
\(n_1^2 + n_2^2 + ... + n_k^2\) cách
-
D.
\({n_1}.{n_2} + {n_2}.{n_3} + ... + {n_{k - 1}}.{n_k}\) cách
Nghiệm của phương trình \(4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\) là:
-
A.
\(x = \pm \dfrac{\pi }{6} + k\pi \,\,\left( {k \in Z} \right)\)
-
B.
\(x = \pm \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in Z} \right)\)
-
C.
\(x = \pm \dfrac{\pi }{3} + k\pi \,\,\left( {k \in Z} \right)\)
-
D.
\(\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \,\,\left( {k \in Z} \right)\\x = \dfrac{\pi }{3} + k\pi \,\,\left( {k \in Z} \right)\end{array} \right.\)
Phương trình \(\cos 2x = 1\) có nghiệm là:
-
A.
\(x = k\pi \left( {k \in Z} \right)\)
-
B.
\(x = \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
C.
\(x = k2\pi \left( {k \in Z} \right)\)
-
D.
\(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
Từ các chữ số $1,2,3,4,5,6,7$ lập được bao nhiêu số tự nhiên gồm $4$ chữ số khác nhau và là số chẵn?
-
A.
$360$
-
B.
$343$
-
C.
$523$
-
D.
$347$
Số tổ hợp chập 6 của 7 phần tử là
-
A.
\(6\)
-
B.
\(7\)
-
C.
\(13\)
-
D.
\(42\)
Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn, mỗi đội chỉ được trình bày 1 vở kịch, 1 điệu múa và 1 bài hát. Hỏi đội văn nghệ trên có bao nhiêu cách chọn chương trình diễn, biết chất lượng các vở kịch, các điệu múa, các bài hát là như nhau?
-
A.
$11$
-
B.
$36$
-
C.
$25$
-
D.
$18$
Chọn mệnh đề đúng:
-
A.
\(\cos x \ne 1 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
B.
\(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
C.
\(\cos x \ne - 1 \Leftrightarrow x \ne - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
D.
\(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
Với giá trị nào của m thì phương trình \(\sqrt 3 \sin 2x - m\cos 2x = 1\) luôn có nghiệm?
-
A.
\(m = 1\)
-
B.
Không có m
-
C.
\(m = 0\)
-
D.
Với mọi m
Cho tập $A = \left\{ {1;2;4;6;7;9} \right\}$. Hỏi có thể lập được từ tập $A$ bao nhiêu số tự nhiên có $4$ chữ số đôi một khác nhau, trong đó không có mặt chữ số $7$.
-
A.
$36$
-
B.
$60$
-
C.
$72$
-
D.
$120$
Hàm số \(y = \dfrac{{1 - \sin 2x}}{{\cos 3x - 1}}\) xác định trên:
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k2\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
Tìm chu kì của hàm số \(y = f\left( x \right) = \tan 2x\).
-
A.
\({T_0} = 2\pi \)
-
B.
\({T_0} = \dfrac{\pi }{2}\)
-
C.
\({T_0} = \pi \)
-
D.
\({T_0} = 4\pi \)
Cho \(C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2\). Khi đó tổng $x + y$ bằng:
-
A.
$3$
-
B.
$ - 8$
-
C.
$11$
-
D.
$ - 3$
Nghiệm của phương trình \(\tan 4x.\cot 2x = 1\) là:
-
A.
\(k\pi ,k \in Z\)
-
B.
\(\dfrac{\pi }{4} + \dfrac{{k\pi }}{2},k \in Z\)
-
C.
\(\dfrac{{k\pi }}{2},k \in Z\)
-
D.
Vô nghiệm
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y = \sqrt {2\sin x + 3} \)
-
A.
\(\max y = \sqrt 5 ,\min y = 1\)
-
B.
\(\max y = \sqrt 5 ,\min y = 0\)
-
C.
\(\max y = \sqrt 5 ,\min y = \sqrt 3 \)
-
D.
\(\max y = \sqrt 5 ,\min y = 3\)
Với \(k,n \in N,2 \le k \le n\) thì giá trị của biểu thức $A = C_n^k + 4C_n^{k - 1} + 6C_n^{k - 2} + 4C_n^{k - 3} + C_n^{k - 4} - C_{n + 4}^k + 1$ bằng?
-
A.
$A = 0$
-
B.
$A = 1$
-
C.
$A = 3$
-
D.
$A = - 1$
Một lớp học có $n$ học sinh $\left( {n > 3} \right)$. Thầy chủ nhiệm cần chọn ra một nhóm và cần cử ra $1$ học sinh trong nhóm đó làm nhóm trưởng. Số học sinh trong mỗi nhóm phải lớn hơn $1$ và nhỏ hơn $n$. Gọi $T$ là số cách chọn. Lúc này:
-
A.
\(T = \sum\limits_{k = 2}^{n - 1} {kC_n^k} \)
-
B.
\(T = n\left( {{2^{n - 1}} - 1} \right)\)
-
C.
\(T = n{2^{n - 1}}\)
-
D.
\(T = \sum\limits_{k = 1}^n {kC_n^k} \)
Gọi $M'$ là ảnh của điểm $M$ qua một phép biến hình. Có tất cả bao nhiêu điểm $M'$?
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(4\)
Cho đường thẳng \(d\) và điểm \(M'\) là ảnh của điểm \(M\) nằm ngoài \(d\) qua phép chiếu vuông góc lên đường thẳng $d$. Chọn mệnh đề đúng:
-
A.
\(MM' \bot d\) tại \(M'\)
-
B.
\(MM' \bot d\) tại \(M\)
-
C.
\(MM'//d\)
-
D.
\(MM' \equiv d\)
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho $T$ là một phép tịnh tiến theo vectơ $\overrightarrow u $ biến điểm $M\left( {x;y} \right)$ thành điểm $M'\left( {x';y'} \right)$ với biểu thức tọa độ là: $x = x' + 3;\,\,y = y' - 5$. Tọa độ của vectơ tịnh tiến $\overrightarrow u $ là:
-
A.
$\left( {5; - 3} \right)$
-
B.
$\left( {3;5} \right)$
-
C.
$\left( { - 3;5} \right)$
-
D.
\(\left( {3; - 5} \right)\)
Cho hai đường thẳng song song $a$ và $b$. Phát biểu nào sau đây là đúng?
-
A.
Không tồn tại phép tịnh tiến nào biến đường thẳng $a$ thành đường thẳng $b$.
-
B.
Có duy nhất một phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
-
C.
Có đúng hai phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
-
D.
Có vô số phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
Trong mặt phẳng với hệ tọa độ $Oxy$, cho parabol $\left( P \right)$ có phương trình $y = {x^2} - x + 1$. Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ $\overrightarrow u = \left( {1; - 2} \right)$ và $\overrightarrow v = \left( {2;3} \right)$, parabol $\left( P \right)$ biến thành parabol $\left( Q \right)$ có phương trình là:
-
A.
\(y = {x^2} - 7x + 14\)
-
B.
\(y = {x^2} + 3x + 2\)
-
C.
\(y = {x^2} + 5x + 6\)
-
D.
\(y = {x^2} - 9x + 5\)
Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} $ là tập nào sau đây?
-
A.
Tập \(\emptyset \)
-
B.
Đường tròn tâm \(A\) bán kính \(AB\)
-
C.
Đường tròn tâm \(B\) bán kính \(R\)
-
D.
Đường tròn tâm \(I\) bán kính \(R\) với \(\overrightarrow {OI} = \overrightarrow {AB} \)
Ảnh $A'$ của $A\left( {4; - 3} \right)$ qua phép đối xứng trục $d$ với \(d:2x\; - y = 0\) có tọa độ là:
-
A.
$A'\left( { - 2;7} \right)$
-
B.
\(A'\left( { - \dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
-
C.
\(A'\left( {\dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
-
D.
\(A'\left( {12;\dfrac{7}{5}} \right)\)
Hình nào sau đây có nhiều trục đối xứng nhất ?
-
A.
Hình thoi
-
B.
Hình vuông
-
C.
Hình elip
-
D.
hình tròn.
Trong mặt phẳng tọa độ \(Oxy\) cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\). Phép đối xứng trục \(Ox\) biến đường tròn \(\left( C \right)\) thành đường tròn \(\left( {C'} \right)\) có phương trình là:
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4.\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 4.\)
Khẳng định nào sau đây sai ?
-
A.
Phép đối xứng trục biến một vector thành một vector bằng nó
-
B.
Phép đối xứng trục biến một đoạn thẳng thành một đoạn thẳng bằng nó
-
C.
Phép đối xứng trục biến một tam giác thành một tam giác bằng nó
-
D.
Phép đối xứng trục biến một đường tròn thành một đường tròn có bán kính bằng với bán kính của nó.
Cho hai đường thẳng $a$ và $b$ cắt nhau tại điểm $O$. Nhận định nào sau đây là đúng?
-
A.
Không có phép đối xứng trục nào biến $a$ thành $b$
-
B.
Có duy nhất một phép đối xứng trục biến $a$ thành $b$
-
C.
Có đúng hai phép đối xứng trục biến $a$ thành $b$
-
D.
Có vô số phép đối xứng trục biến $a$ thành $b$ .
Điểm nào là ảnh của \(M\left( {3; - 1} \right)\) qua phép đối xứng tâm \(I\left( {1;2} \right)\)
-
A.
\(\left( {2;1} \right)\)
-
B.
\(\left( { - 1;5} \right)\)
-
C.
\(\left( { - 1;3} \right)\)
-
D.
\(\left( {5; - 4} \right)\)
Trong mặt phẳng tọa độ $Oxy$, nếu phép đối xứng tâm biến điểm \(A\left( {5;2} \right)\) thành điểm \(A'\left( { - 3;4} \right)\) thì nó biến điểm \(B\left( {1; - 1} \right)\) thành điểm :
-
A.
\(B'\left( {1;7} \right)\)
-
B.
\(B'\left( {1;6} \right)\)
-
C.
\(B'\left( {2;5} \right)\)
-
D.
\(B'\left( {1; - 5} \right)\)
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó
-
A.
Không có phép nào
-
B.
Có một phép duy nhất
-
C.
Chỉ có hai phép
-
D.
Có vô số phép.
Cho hai khẳng định sau:
(I) Nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng.
(II) Cho phép đối xứng tâm ${D_O}$ và đường thẳng $d$ không đi qua $O$. Có thể dựng $d'$ là ảnh của $d$ qua ${D_O}$ mà chỉ sử dụng compa một lần và thước hai lần.
Chọn kết luận đúng:
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
Cả hai đều đúng
-
D.
Cả hai đều sai
Trong mặt phẳng $Oxy$ cho hai đường thẳng \(a:\,\,2x + y + 5 = 0\) và \(b:\,\,x - 2y - 3 = 0\). Nếu có một phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc đó có thể là góc nào trong các góc cho dưới đây:
-
A.
\({45^0}\)
-
B.
\({90^0}\)
-
C.
\({120^0}\)
-
D.
\({60^0}\)
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
-
A.
\(M'\left( { - 1; - 1} \right)\)
-
B.
\(M'\left( {1;1} \right)\)
-
C.
\(M'\left( { - 1;1} \right)\)
-
D.
\(M'\left( {1;0} \right)\)
Trong mặt phẳng $Oxy$ cho đường thẳng \(d:\,\,x - y + 4 = 0\). Hỏi trong $4$ đường thẳng cho bởi các phương trình sau, đường thẳng nào có thể biến thành $d$ qua phép quay tâm \(I\left( {0;3} \right)\) góc quay \(\pi \) ?
-
A.
\(2x + y - 4 = 0\)
-
B.
\(2x + 2y - 3 = 0\)
-
C.
\(x - y + 2 = 0\)
-
D.
\(2x - 2y + 1 = 0\)
Khẳng định nào sai ?
-
A.
Phép tịnh tiến một đoạn thẳng thành một đoạn thẳng bằng nó
-
B.
Phép quay biến đường thẳng thành đường thẳng song song với nó
-
C.
Phép tịnh tiến biến tam giác thành tam giác bằng nó.
-
D.
Phép quay biến đường tròn thành đường tròn có cùng bán kính.
Trong mặt phẳng $Oxy$ cho điểm \(M\left( { - 2;4} \right)\). Phép vị tự tâm $O$ tỉ số \(k = - 2\) biến điểm $M$ thành điểm nào trong các điểm sau?
-
A.
\(\left( { - 3;4} \right)\)
-
B.
\(\left( { - 4; - 8} \right)\)
-
C.
\(\left( {4; - 8} \right)\)
-
D.
\(\left( {4;8} \right)\)
Trong mặt phẳng tọa độ \(Oxy\) cho phép vị tự \(V\) tỉ số \(k = 2\) biến điểm \(A\left( {1; - 2} \right)\) thành điểm \(A'\left( { - 5;1} \right).\) Hỏi phép vị tự \(V\) biến điểm \(B\left( {0;1} \right)\) thành điểm có tọa độ nào sau đây?
-
A.
\(\left( {0;2} \right).\)
-
B.
\(\left( {12; - 5} \right).\)
-
C.
\(\left( { - 7;7} \right).\)
-
D.
\(\left( {11;6} \right).\)
Trong mặt phẳng tọa độ $Oxy$. Cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt có phương trình \(x - 2y + 1 = 0\) và \(x - 2y + 4 = 0\), điểm \(I\left( {2;1} \right)\). Phép vị tự tâm $I$ tỉ số $k$ biến đường thẳng \({\Delta _1}\) thành \({\Delta _2}\) khi đó giá trị của $k$ là :
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Cho tam giác $ABC$ có trực tâm $H$, trọng tâm $G$ và tâm đường tròn ngoại tiếp $O$ . Phép vị tự tâm $G$ biến $H$ thành $O$ có tỉ số là :
-
A.
$2$
-
B.
\(\dfrac{1}{2}\)
-
C.
\( - \dfrac{1}{2}\)
-
D.
\( - \dfrac{2}{3}\)
Mệnh đề nào sau đây là đúng?
-
A.
Phép đồng dạng tỉ số \(k = 1\) là phép dời hình.
-
B.
Phép đồng dạng tỉ số \(k = - 1\) là phép đối xứng tâm.
-
C.
Phép đồng dạng tỉ số \(k = 1\) là phép tịnh tiến
-
D.
Phép đồng dạng tỉ số \(k = 1\) là phép vị tự tỉ số \(k = 1\)
Cho $\Delta ABC$ đều cạnh $2$. Qua ba phép đồng dạng liên tiếp: Phép tịnh tiến ${T_{\overrightarrow {BC} }}$, phép quay $Q\left( {B,{{60}^0}} \right)$, phép vị tự ${V_{\left( {A,\,3} \right)}},\Delta ABC$ biến thành $\Delta {A_1}{B_1}{C_1}$. Diện tích $\Delta {A_1}{B_1}{C_1}$ là:
-
A.
$5\sqrt 2 $
-
B.
$9\sqrt 3 $
-
C.
$9\sqrt 2 $
-
D.
$5\sqrt 3 $
Trong mặt phẳng \(Oxy,\) cho đường thẳng \(d:2x - y = 0\). Phương trình đường thẳng qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm \(O\) tỉ số \(k = - 2\) và phép đối xứng trục \(Oy\) là đường thẳng nào sau đây?
-
A.
\( -2x - y = 0\).
-
B.
\(2x - y = 0\).
-
C.
\(4x - y = 0\).
-
D.
\(2x + y - 2 = 0\)
Cho phương trình \(\sin \left( {2x - \dfrac{\pi }{5}} \right) = 3{m^2} + \dfrac{m}{2}\). Biết \(x = \dfrac{{11\pi }}{{60}}\) là một nghiệm của phương trình. Tính \(m\).
-
A.
\(\left[ \begin{array}{l}m = 1\\m = \dfrac{1}{2}\end{array} \right.\)
-
B.
\(\left[ \begin{array}{l}m = - \dfrac{3}{2}\\m = 0\end{array} \right.\)
-
C.
\(\left[ \begin{array}{l}m = - \dfrac{1}{4}\\m = \dfrac{2}{3}\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l}m = - \dfrac{1}{2}\\m = \dfrac{1}{3}\end{array} \right.\)
Giải phương trình \(\cos 2x + \cos 4x + \cos 6x = \cos x\cos 2x\cos 3x + 2\).
-
A.
\(x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
B.
\(x = \dfrac{2\pi }{{3}} + 2k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
C.
\(x =\dfrac{{\pi }}{3} + 2k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
D.
\(x = \dfrac{k\pi }{{3}} \,\,\left( {k \in \mathbb{Z}} \right)\).
Có bao nhiêu cách xếp \(5\) học sinh thành một hàng dọc?
-
A.
\(1\).
-
B.
\(25\).
-
C.
\(5\).
-
D.
\(120\).
Số (5! – P4) bằng:
-
A.
5
-
B.
12
-
C.
24
-
D.
96
Cho hình bình hành ABCD. Phép tịnh tiến theo \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\) biến đoạn thẳng DC thành đoạn thẳng nào sau đây?
-
A.
BC
-
B.
AB
-
C.
DC
-
D.
CA
Lời giải và đáp án
Số các hoán vị khác nhau của \(n\) phần tử là:
-
A.
\({P_n} = n!\)
-
B.
\({P_n} = n\)
-
C.
\({P_n} = \left( {n - 1} \right)!\)
-
D.
\({P_n} = {n^2}\)
Đáp án : A
Số các hoán vị khác nhau của \(n\) phần tử là \({P_n} = n!\)
Một số em có thể sẽ chọn nhầm đáp án B vì nhớ nhầm công thức tính số hoán vị.
Để phương trình \(\dfrac{{{a^2}}}{{1 - {{\tan }^2}x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\) có nghiệm, tham số a phải thỏa mãn điều kiện:
-
A.
\(\left| a \right| \ge 1\)
-
B.
\(\left| a \right| > 1\)
-
C.
\(\left| a \right| = 1\)
-
D.
\(\left| a \right| \ne 1\)
Đáp án : B
- Tìm ĐKXĐ của phương trình.
- Biến đổi phương trình đã cho về phương trình đối với chỉ một hàm số lượng giác.
$\left\{ \begin{array}{l}1 - {\tan ^2}x \ne 0\\\cos 2x \ne 0\\\cos x \ne 0\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}\dfrac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}} \ne 0\\\cos 2x \ne 0\\\cos x \ne 0\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}\cos 2x \ne 0\\\cos x \ne 0\end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}2x \ne \dfrac{\pi }{2} + k\pi \\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\\x \ne \dfrac{\pi }{2} + k\pi \end{array} \right.\,\,\,\left( {k \in Z} \right)$
$\begin{array}{l}\dfrac{{{a^2}}}{{1 - {{\tan }^2}x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}} \Leftrightarrow \dfrac{{{a^2}}}{{\dfrac{{{{\cos }^2}x - {{\sin }^2}x}}{{{{\cos }^2}x}}}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}}\\ \Leftrightarrow \dfrac{{{a^2}{{\cos }^2}x}}{{\cos 2x}} = \dfrac{{{{\sin }^2}x + {a^2} - 2}}{{\cos 2x}} \Leftrightarrow {a^2}{\cos ^2}x = {\sin ^2}x + {a^2} - 2\\ \Leftrightarrow {a^2}{\cos ^2}x = 1 - {\cos ^2}x + {a^2} - 2\\ \Leftrightarrow \left( {{a^2} + 1} \right){\cos ^2}x = {a^2} - 1 \Leftrightarrow {\cos ^2}x = \dfrac{{{a^2} - 1}}{{{a^2} + 1}} < 1\end{array}$
Vì \(\cos x \ne 0 \Rightarrow 0 < {\cos ^2}x \le 1 \Leftrightarrow {\cos ^2}x > 0 \Leftrightarrow {a^2} - 1 > 0 \Rightarrow \left| a \right| > 1\)
Một số em có thể sẽ chọn nhầm đáp án A vì quên mất điều kiện \(\cos x \ne 0\).
Với giá trị của $x$ thỏa mãn \(12C_x^1 + C_{x + 4}^2 = 162\) thì \(A_{x - 1}^2 - C_x^1 = ?\)
-
A.
$20$
-
B.
$30$
-
C.
$ - 10$
-
D.
$34$
Đáp án : D
Áp dụng các công thức chỉnh hợp và tổ hợp: \(A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}\,;\,C_n^k = \dfrac{{n!}}{{k!\left( {n - k} \right)!}}\) để tìm x, sau đó thay vào tính giá trị biểu thức
\(\begin{array}{l}12C_x^1 + C_{x + 4}^2 = 162\\ \Leftrightarrow 12x + \dfrac{{\left( {x + 4} \right)!}}{{2!\left( {x + 2} \right)!}} = 162\\ \Leftrightarrow 12x + \dfrac{{\left( {x + 4} \right)\left( {x + 3} \right)}}{2} = 162\\ \Leftrightarrow 24x + {x^2} + 7x + 12 = 324\\ \Leftrightarrow {x^2} + 31x - 312 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 8\,\,\,\,\,\,\,\,\,\left( {tm} \right)\\x = - 39\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
\( \Rightarrow A_{x - 1}^2 - C_x^1 = A_7^2 - C_8^1 = 34\)
Công việc \(A\) có \(k\) công đoạn \({A_1},{A_2},...,{A_k}\) với số cách thực hiện lần lượt là \({n_1},{n_2},...,{n_k}\). Khi đó số cách thực hiện công việc \(A\) là:
-
A.
\({n_1} + {n_2} + ... + {n_k}\) cách
-
B.
\({n_1}.{n_2}.....{n_k}\) cách
-
C.
\(n_1^2 + n_2^2 + ... + n_k^2\) cách
-
D.
\({n_1}.{n_2} + {n_2}.{n_3} + ... + {n_{k - 1}}.{n_k}\) cách
Đáp án : B
Số cách thực hiện công việc \(A\) là: \({n_1}.{n_2}.....{n_k}\) cách.
Một số em có thể sẽ chọn nhầm đáp án A vì áp dụng nhầm sang công thức cộng.
Nghiệm của phương trình \(4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\) là:
-
A.
\(x = \pm \dfrac{\pi }{6} + k\pi \,\,\left( {k \in Z} \right)\)
-
B.
\(x = \pm \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in Z} \right)\)
-
C.
\(x = \pm \dfrac{\pi }{3} + k\pi \,\,\left( {k \in Z} \right)\)
-
D.
\(\left[ \begin{array}{l}x = \dfrac{\pi }{6} + k\pi \,\,\left( {k \in Z} \right)\\x = \dfrac{\pi }{3} + k\pi \,\,\left( {k \in Z} \right)\end{array} \right.\)
Đáp án : A
Bước 1: Sử dụng các công thức biến đổi lượng giác để biến đổi phương trình thành phương trình bậc hai đối với \(\cos 2x\).
Các công thức:
\({\sin ^2}x + {\cos ^2}x = 1\)
${\cos ^2}x =\dfrac{{1 + \cos 2x}}{2} $
Bước 2: Đặt \(t = \cos 2x\left( { - 1 \le t \le t} \right)\), giải phương trình ẩn \(t\) rồi giải phương trình tìm \(x\).
$\cos x= \cos a \Leftrightarrow x=\pm a+ k2\pi$
Bước 1:
\(\begin{array}{l}4{\sin ^2}2x + 8{\cos ^2}x - 9 = 0\\ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 8.\dfrac{{1 + \cos 2x}}{2} - 9 = 0\\ \Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4\left( {1 + \cos 2x} \right) - 9 = 0\\\Leftrightarrow 4\left( {1 - {{\cos }^2}2x} \right) + 4 + 4\cos 2x - 9 = 0\\ \Leftrightarrow 4 - 4{\cos ^2}2x + 4\cos 2x - 5 = 0 \\\Leftrightarrow - 4{\cos ^2}2x + 4\cos 2x - 1 = 0\end{array}\)
Bước 2:
Đặt \(\cos 2x = t\,\,\left( { - 1 \le t \le 1} \right)\) khi đó phương trình có dạng
\( - 4{t^2} + 4t - 1 = 0 \)\( \Leftrightarrow - \left( {4{t^2} - 4t + 1} \right) = 0\)\(\Leftrightarrow - {\left( {2t - 1} \right)^2} = 0 \) \(\Leftrightarrow t = \dfrac{1}{2}\left( {tm} \right)\)
\(\begin{array}{l} \Leftrightarrow \cos 2x = \dfrac{1}{2} \Leftrightarrow \cos 2x =\cos \dfrac{\pi }{3} \\\Leftrightarrow 2x = \pm \dfrac{\pi }{3} + k2\pi \Leftrightarrow x = \pm \dfrac{\pi }{6} + k\pi \left( {k \in Z} \right)\end{array}\)
Phương trình \(\cos 2x = 1\) có nghiệm là:
-
A.
\(x = k\pi \left( {k \in Z} \right)\)
-
B.
\(x = \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
C.
\(x = k2\pi \left( {k \in Z} \right)\)
-
D.
\(x = \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
Đáp án : A
Ta có: \(\cos 2x = 1 \Leftrightarrow \cos 2x = \cos 0 \Leftrightarrow 2x = k2\pi \Leftrightarrow x = k\pi \left( {k \in Z} \right)\)
Một số em có thể sẽ chọn nhầm đáp án C vì quên không chia cho \(2\) khi tính \(x\), hoặc một số em khác thì chọn nhầm đáp án D vì giải sai phương trình \(\cos 2x = 1 \Leftrightarrow \cos 2x = \cos \dfrac{\pi }{2}\) là sai.
Từ các chữ số $1,2,3,4,5,6,7$ lập được bao nhiêu số tự nhiên gồm $4$ chữ số khác nhau và là số chẵn?
-
A.
$360$
-
B.
$343$
-
C.
$523$
-
D.
$347$
Đáp án : A
Sử dụng quy tắc nhân với chú ý có bốn công đoạn để lập được số thỏa mãn bài toán.
Gọi số tự nhiên có $4$ chữ số cần tìm là \(\overline {abcd} \,\,\left( {a \ne 0,a \ne b \ne c \ne d} \right)\), \(d \in \left\{ {2;4;6} \right\}\)
Vì \(\overline {abcd} \) là số chẵn nên \(d \in \left\{ {2;4;6} \right\} \)
\(\Rightarrow \) Có $3$ cách chọn $d.$
Vì $a \ne d$ nên có $6$ cách chọn $a$
$b\ne a, d$ nên có $5$ cách chọn $b$
$c \ne a, b, d$ nên có $4$ cách chọn $c$
Áp dụng quy tắc nhân ta có số các số thỏa mãn là: $3.6.5.4 = 360$ (số)
Đối với bài toán này, vì số cần lập là số chẵn nên ta ưu tiên chọn $d$ trước rồi mới đến các chữ số khác.
Số tổ hợp chập 6 của 7 phần tử là
-
A.
\(6\)
-
B.
\(7\)
-
C.
\(13\)
-
D.
\(42\)
Đáp án : B
Sử dụng công thức tính số tổ hợp chập k của n phần tử \(C_n^k\).
Số tổ hợp chập 6 của 7 phần tử là \(C_7^6 = 7\).
Một số em có thể chọn nhầm đáp án A vì tính sai \(C_7^6\).
Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn, mỗi đội chỉ được trình bày 1 vở kịch, 1 điệu múa và 1 bài hát. Hỏi đội văn nghệ trên có bao nhiêu cách chọn chương trình diễn, biết chất lượng các vở kịch, các điệu múa, các bài hát là như nhau?
-
A.
$11$
-
B.
$36$
-
C.
$25$
-
D.
$18$
Đáp án : B
Chọn 1 vở kịch có 2 cách.
Chọn 1 điệu múa có 3 cách.
Chọn 1 bài hát có 6 cách.
Vậy theo quy tắc nhân ta có: 2.3.6 = 36 cách.
Một số em có thể chọn nhầm đáp án A vì áp dụng nhầm công thức cộng.
Chọn mệnh đề đúng:
-
A.
\(\cos x \ne 1 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
B.
\(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\)
-
C.
\(\cos x \ne - 1 \Leftrightarrow x \ne - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
-
D.
\(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\)
Đáp án : B
Ta có:
+) \(\cos x \ne 1 \Leftrightarrow x \ne k2\pi \left( {k \in Z} \right)\) nên A sai.
+) \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)\) nên B đúng, D sai.
+) \(\cos x \ne - 1 \Leftrightarrow x \ne \pi + k2\pi \left( {k \in Z} \right)\) nên C sai.
Một số em có thể sẽ chọn nhầm đáp án C vì nghĩ rằng \(\cos x \ne - 1 \Leftrightarrow x \ne - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)\) là sai.
Với giá trị nào của m thì phương trình \(\sqrt 3 \sin 2x - m\cos 2x = 1\) luôn có nghiệm?
-
A.
\(m = 1\)
-
B.
Không có m
-
C.
\(m = 0\)
-
D.
Với mọi m
Đáp án : D
Điều kiện để phương trình \(a\cos x + b\sin x = c\) có nghiệm là \({a^2} + {b^2} \ge {c^2}\)
\(\sqrt 3 \sin 2x - m\cos 2x = 1\)
Ta có: \(\left\{ \begin{array}{l}a = \sqrt 3 \\b = - m\\c = 1\end{array} \right.\)
Để phương trình có nghiệm thì \({a^2} + {b^2} \ge {c^2} \Leftrightarrow 3 + {m^2} \ge 1 \Leftrightarrow {m^2} \ge - 2\) (luôn đúng với \(\forall m\) )
Vậy phương trình luôn có nghiệm với mọi $m$.
Cho tập $A = \left\{ {1;2;4;6;7;9} \right\}$. Hỏi có thể lập được từ tập $A$ bao nhiêu số tự nhiên có $4$ chữ số đôi một khác nhau, trong đó không có mặt chữ số $7$.
-
A.
$36$
-
B.
$60$
-
C.
$72$
-
D.
$120$
Đáp án : D
Đưa về bài toán lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau từ tập $B = \left\{ {1;2;4;6;9} \right\}$.
Sử dụng công thức chỉnh hợp cho bài toán này.
Lập số tự nhiên có $4$ chữ số đôi một khác nhau sao cho không có mặt chữ số $7$, ta bỏ chữ số $7$ ra khổi tập hợp $A$, khi đó ta được tập hợp $B = \left\{ {1;2;4;6;9} \right\}$ và đưa bài toán trở thành có thể lập được từ tập $B$ bao nhiêu số tự nhiên có $4$ chữ số đôi một khác nhau.
Số các số có $4$ chữ số khác nhau lập được từ tập $B$ là chỉnh hợp chập $4$ của $5$. Vậy có \(A_5^4 = 120\) số.
Số các số cần tìm ở đây chính là số cách chọn $4$ trong $5$ chữ số ở tập hợp $B$, hơn nữa các chữ số đều có phân biệt thứ tự nên ta sẽ dùng công thức chỉnh hợp chứ không phải tổ hợp.
Hàm số \(y = \dfrac{{1 - \sin 2x}}{{\cos 3x - 1}}\) xác định trên:
-
A.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k2\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
B.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
C.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{3},k \in \mathbb{Z}} \right\}\)
-
D.
\(D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)
Đáp án : A
Hàm số \(y = \dfrac{1}{{f\left( x \right)}}\) xác định nếu \(f\left( x \right) \ne 0\).
Sử dụng công thức $\cos a \ne 1 \Leftrightarrow a \ne k2\pi$
Điều kiện: \(\cos 3x - 1 \ne 0 \Leftrightarrow \cos 3x \ne 1 \Leftrightarrow 3x \ne k2\pi \Leftrightarrow x \ne \dfrac{{k2\pi }}{3}\)
Một số em chỉ nghĩ rằng hàm số xác định nếu \(\cos 3x \ne 0 \Leftrightarrow 3x \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow x \ne \dfrac{\pi }{6} + \dfrac{{k\pi }}{3}\) và chọn nhầm đáp án B là sai.
Một số em khác sẽ biến đổi \(\cos 3x - 1 \ne 0 \Leftrightarrow \cos 3x \ne 1 \Leftrightarrow 3x \ne k\pi \Leftrightarrow x \ne \dfrac{{k\pi }}{3}\) và chọn C là sai.
Tìm chu kì của hàm số \(y = f\left( x \right) = \tan 2x\).
-
A.
\({T_0} = 2\pi \)
-
B.
\({T_0} = \dfrac{\pi }{2}\)
-
C.
\({T_0} = \pi \)
-
D.
\({T_0} = 4\pi \)
Đáp án : B
Hàm số \(y = \tan \left( {ax + b} \right),y = \cot \left( {ax + b} \right)\) tuần hoàn với chu kỳ \(T = \dfrac{\pi }{{\left| a \right|}}\).
Chu kì của hàm số \(f\left( x \right) = \tan 2x\) là \({T_0} = \dfrac{\pi }{2}\)
Một số em có thể nhớ nhầm công thức chu kì của hàm số \(y = \tan \left( {ax + b} \right),y = \cot \left( {ax + b} \right)\) là \(T = \left| a \right|\pi \) dẫn đến chọn nhầm đáp án A là sai.
Cho \(C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2\). Khi đó tổng $x + y$ bằng:
-
A.
$3$
-
B.
$ - 8$
-
C.
$11$
-
D.
$ - 3$
Đáp án : C
Áp dụng các công thức chỉnh hợp và tổ hợp: \(A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}\,;\,C_n^k = \dfrac{{n!}}{{k!\left( {n - k} \right)!}}\)
Và áp dụng công thức của tỉ lệ thức: $a:b:c = x:y:z \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = \dfrac{x}{y}\\\dfrac{a}{c} = \dfrac{x}{z}\\\dfrac{b}{c} = \dfrac{y}{z}\end{array} \right.$
ĐK: \(\left\{ \begin{array}{l}x + 1 \ge y \ge 0\\x \ge y + 1 \ge 0\\x \ge y - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \ge 1\\x \ge y + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y \ge 1\\x \ge 2\end{array} \right.\,\,\left( {x,y \in N} \right)\)
\(\begin{array}{l}C_{x + 1}^y:C_x^{y + 1}:C_x^{y - 1} = 6:5:2 \Rightarrow \left\{ \begin{array}{l}\dfrac{{C_{x + 1}^y}}{{C_x^{y + 1}}} = \dfrac{6}{5}\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\dfrac{{C_{x + 1}^y}}{{C_x^{y - 1}}} = \dfrac{6}{2} = 3\,\,\left( 2 \right)\end{array} \right.\\\left( 1 \right) \Leftrightarrow \dfrac{{\dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}}}{{\dfrac{{x!}}{{\left( {y + 1} \right)!\left( {x - y - 1} \right)!}}}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}.\dfrac{{\left( {y + 1} \right)!\left( {x - y - 1} \right)!}}{{x!}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)\left( {y + 1} \right)}}{{\left( {x - y} \right)\left( {x - y + 1} \right)}} = \dfrac{6}{5}\,\,\,\left( 3 \right)\\\left( 2 \right) \Leftrightarrow \dfrac{{\dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}}}{{\dfrac{{x!}}{{\left( {y - 1} \right)!\left( {x - y + 1} \right)!}}}} = 3\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)!}}{{y!\left( {x + 1 - y} \right)!}}\dfrac{{\left( {y - 1} \right)!\left( {x - y + 1} \right)!}}{{x!}} = 3\\ \Leftrightarrow \dfrac{{x + 1}}{y} = 3 \Rightarrow x = 3y - 1\end{array}\)
Thay vào (3) ta có:
\(\begin{array}{l}\dfrac{{3y\left( {y + 1} \right)}}{{\left( {2y - 1} \right)2y}} = \dfrac{6}{5}\\ \Leftrightarrow \dfrac{{y + 1}}{{4y - 2}} = \dfrac{2}{5} \Leftrightarrow 5y + 5 = 8y - 4\\ \Leftrightarrow 3y = 9 \Leftrightarrow y = 3\,\,\left( {tm} \right) \Rightarrow x = 8\,\,\left( {tm} \right)\\ \Rightarrow x + y = 11\end{array}\)
Nghiệm của phương trình \(\tan 4x.\cot 2x = 1\) là:
-
A.
\(k\pi ,k \in Z\)
-
B.
\(\dfrac{\pi }{4} + \dfrac{{k\pi }}{2},k \in Z\)
-
C.
\(\dfrac{{k\pi }}{2},k \in Z\)
-
D.
Vô nghiệm
Đáp án : D
- Tìm điều kiện xác định của phương trình.
- Sử dụng công thức \(\tan u.\cot u = 1\) để biến đổi phương trình về dạng phương trình lượng giác cơ bản $\tan x=\tan y$
- Giải phương trình $\tan x=\tan y$$ \Leftrightarrow x=y+k\pi$, $k \in \mathbb{Z}$
- Kiểm tra điều kiện và loại nghiệm.
ĐKXĐ: \(\left\{ \begin{array}{l}\cos 4x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x \ne \dfrac{\pi }{2} + k\pi \\2x \ne k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\\x \ne \dfrac{{k\pi }}{2}\end{array} \right.\)
Khi đó, dễ thấy \(\cot 2x \ne 0\) (Nếu \(\cot 2x = 0\) thì phương trình thành 0=1 =>Vô nghiệm) nên phương trình tương đương:
\(\tan 4x.\cot 2x = 1 \Leftrightarrow \tan 4x = \dfrac{1}{{\cot 2x}} \\ \Leftrightarrow \tan 4x = \tan 2x \Leftrightarrow 4x = 2x + k\pi \\ \Leftrightarrow x = \dfrac{{k\pi }}{2}\)
Kết hợp với điều kiện ta được phương trình vô nghiệm.
Nhiều em HS có thể sẽ không tìm ĐKXĐ dẫn đến không kết hợp điều kiện loại nghiệm và chọn nhầm đáp án C là sai.
Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau \(y = \sqrt {2\sin x + 3} \)
-
A.
\(\max y = \sqrt 5 ,\min y = 1\)
-
B.
\(\max y = \sqrt 5 ,\min y = 0\)
-
C.
\(\max y = \sqrt 5 ,\min y = \sqrt 3 \)
-
D.
\(\max y = \sqrt 5 ,\min y = 3\)
Đáp án : A
Sử dụng \( - 1 \le \sin x \le 1\) để đánh giá biểu thức \(\sqrt {2\sin x + 3} \), từ đó tìm được GTNN, GTLN của hàm số.
Do \( - 1 \le \sin x \le 1 \Rightarrow -2 \le 2\sin x \le 2 \)\(\Rightarrow -2+3 \le2\sin x + 3 \le 2+3 \)\(\Rightarrow1 \le \sqrt {2\sin x + 3} \le \sqrt 5 \).
Dấu “=” xảy ra khi lần lượt \(\sin x = - 1\) và $\sin x = 1$
Một số em có thể sẽ đánh giá \(\sqrt {2\sin x + 3} \ge 0,\forall x\) nên chọn nhầm đáp án B là sai.
Với \(k,n \in N,2 \le k \le n\) thì giá trị của biểu thức $A = C_n^k + 4C_n^{k - 1} + 6C_n^{k - 2} + 4C_n^{k - 3} + C_n^{k - 4} - C_{n + 4}^k + 1$ bằng?
-
A.
$A = 0$
-
B.
$A = 1$
-
C.
$A = 3$
-
D.
$A = - 1$
Đáp án : B
Đối với những bài toán tổng những tổ hợp có chỉ số trên và chỉ số dưới là những số tự nhiên liên tiếp ta sử dụng công thức \(C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}\)
Trước hết ta chứng minh công thức \(C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}\)
\(\begin{array}{l}VT = C_n^k + C_n^{k + 1}\\ = \dfrac{{n!}}{{k!\left( {n - k} \right)!}} + \dfrac{{n!}}{{\left( {k + 1} \right)!\left( {n - k - 1} \right)!}}\\ = \dfrac{{n!}}{{k!\left( {n - k - 1} \right)!}}\left( {\dfrac{1}{{n - k}} + \dfrac{1}{{k + 1}}} \right)\\ = \dfrac{{n!}}{{k!\left( {n - k - 1} \right)!}}.\dfrac{{k + 1 + n - k}}{{\left( {n - k} \right)\left( {k + 1} \right)}}\\ = \dfrac{{n!\left( {n + 1} \right)}}{{k!\left( {k + 1} \right)\left( {n - k - 1} \right)!\left( {n - k} \right)}}\\ = \dfrac{{\left( {n + 1} \right)!}}{{\left( {k + 1} \right)!\left( {n - k} \right)!}} = C_{n + 1}^{k + 1} = VP\end{array}\)
Ta tính giá trị của biểu thức B sau đây:
$\begin{array}{l}B = C_n^k + 4C_n^{k - 1} + 6C_n^{k - 2} + 4C_n^{k - 3} + C_n^{k - 4}\\\,\,\,\,\, = C_n^k + C_n^{k - 1} + 3\left( {C_n^{k - 1} + C_n^{k - 2}} \right) + 3\left( {C_n^{k - 2} + C_n^{k - 3}} \right) + C_n^{k - 3} + C_n^{k - 4}\\\,\,\,\,\, = C_{n + 1}^k + 3C_{n + 1}^{k - 1} + 3C_{n + 1}^{k - 2} + C_{n + 1}^{k - 3}\\\,\,\,\,\, = C_{n + 1}^k + C_{n + 1}^{k - 1} + 2\left( {C_{n + 1}^{k - 1} + C_{n + 1}^{k - 2}} \right) + C_{n + 1}^{k - 2} + C_{n + 1}^{k - 3}\\\,\,\,\,\, = C_{n + 2}^k + 2C_{n + 2}^{k - 1} + C_{n + 2}^{k - 2}\\\,\,\,\,\, = C_{n + 1}^k + C_{n + 1}^{k - 1} + C_{n + 1}^{k - 1} + C_{n + 1}^{k - 2}\\\,\,\,\,\, = C_{n + 3}^k + C_{n + 3}^{k - 1}\\\,\,\,\,\, = C_{n + 4}^k\\ \Rightarrow A = B - C_{n + 4}^k + 1 = C_{n + 4}^k - C_{n + 4}^k + 1 = 1\end{array}$
Khi thực hành thì bước chứng minh công thức \(C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}\) có thể bỏ qua, các em có thể áp dụng trực tiếp coi như một tính chất.
Một lớp học có $n$ học sinh $\left( {n > 3} \right)$. Thầy chủ nhiệm cần chọn ra một nhóm và cần cử ra $1$ học sinh trong nhóm đó làm nhóm trưởng. Số học sinh trong mỗi nhóm phải lớn hơn $1$ và nhỏ hơn $n$. Gọi $T$ là số cách chọn. Lúc này:
-
A.
\(T = \sum\limits_{k = 2}^{n - 1} {kC_n^k} \)
-
B.
\(T = n\left( {{2^{n - 1}} - 1} \right)\)
-
C.
\(T = n{2^{n - 1}}\)
-
D.
\(T = \sum\limits_{k = 1}^n {kC_n^k} \)
Đáp án : A
Thầy chủ nhiệm cần chọn ra một nhóm mà chưa biết nhóm này có bao nhiêu học sinh nên sẽ có các phương án:
PA 1: Nhóm có $2$ học sinh
PA 2: Nhóm có $3$ học sinh.
PA 3: Nhóm có $4$ học sinh.
….
PA (n-2): Nhóm có $n-1$ học sinh.
Tính số cách thực hiện của mỗi phương án sau đó áp dụng quy tắc cộng.
Gọi \({A_k}\) là phương án: Chọn nhóm có $k$ học sinh và chỉ định $1$ bạn trong k học sinh đó làm nhóm trưởng.
Thầy chủ nhiệm có các phương án: \({A_2},{A_3},{A_4},...,{A_{n - 1}}\)
Ta tính xem \({A_k}\) có bao nhiêu cách thực hiện.
Phương án \({A_k}\) có hai công đoạn:
Công đoạn 1: Chọn $k$ học sinh trong $n$ học sinh có \(C_n^k\) cách chọn.
Công đoạn 2: Chọn $1$ học sinh trong $k$ học sinh làm nhóm trưởng có \(C_k^1 = k\) cách.
Theo quy tắc nhân thì phương án \({A_k}\) có \(kC_n^k\) cách thực hiện.
Các phương án \({A_k}\) là độc lập với nhau.
Vậy theo quy tắc cộng ta có: \(T = \sum\limits_{k = 2}^{n - 1} {kC_n^k} \)
Bài toán này cần áp dụng cả quy tắc nhân và quy tắc cộng nên các em phải phân biệt thật rõ hai quy tắc này.
Gọi $M'$ là ảnh của điểm $M$ qua một phép biến hình. Có tất cả bao nhiêu điểm $M'$?
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(4\)
Đáp án : B
Phép biến hình (trong mặt phẳng) là một quy tắc để với mỗi điểm \(M\) thuộc mặt phẳng, xác định được một điểm duy nhất \(M'\) thuộc mặt phẳng ấy
Cho đường thẳng \(d\) và điểm \(M'\) là ảnh của điểm \(M\) nằm ngoài \(d\) qua phép chiếu vuông góc lên đường thẳng $d$. Chọn mệnh đề đúng:
-
A.
\(MM' \bot d\) tại \(M'\)
-
B.
\(MM' \bot d\) tại \(M\)
-
C.
\(MM'//d\)
-
D.
\(MM' \equiv d\)
Đáp án : A
Sử dụng định nghĩa phép chiếu vuông góc: Cho đường thẳng \(d\). Với mỗi điểm \(M\), xác định điểm \(M'\) là hình chiếu của \(M\) lên \(d\). Phép biến hình này là phép chiếu vuông góc lên đường thẳng \(d\).
Từ định nghĩa phép chiếu vuông góc ta thấy \(MM'\) vuông góc với \(d\) tại \(M'\) (vì \(M'\) là hình chiếu của \(M\) trên \(d\) nên \(M' \in d\)).
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng \(M \in d\) là sai
Trong mặt phẳng với hệ tọa độ $Oxy$ , cho $T$ là một phép tịnh tiến theo vectơ $\overrightarrow u $ biến điểm $M\left( {x;y} \right)$ thành điểm $M'\left( {x';y'} \right)$ với biểu thức tọa độ là: $x = x' + 3;\,\,y = y' - 5$. Tọa độ của vectơ tịnh tiến $\overrightarrow u $ là:
-
A.
$\left( {5; - 3} \right)$
-
B.
$\left( {3;5} \right)$
-
C.
$\left( { - 3;5} \right)$
-
D.
\(\left( {3; - 5} \right)\)
Đáp án : C
Sử dụng biểu thức tọa độ của phép tịnh tiến \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}x = x' + 3\\y = y' - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x' = x - 3\\y' = y + 5\end{array} \right. \Rightarrow \overrightarrow u = \left( { - 3;5} \right)\)
Một số em có thể sẽ chọn nhầm đáp án D vì nhớ nhầm biểu thức tọa độ của phép tịnh tiến.
Cho hai đường thẳng song song $a$ và $b$. Phát biểu nào sau đây là đúng?
-
A.
Không tồn tại phép tịnh tiến nào biến đường thẳng $a$ thành đường thẳng $b$.
-
B.
Có duy nhất một phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
-
C.
Có đúng hai phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
-
D.
Có vô số phép tịnh tiến biến đường thẳng $a$ thành đường thẳng $b$.
Đáp án : D
Sử dụng tính chất phép tịnh tiến: biến đường thẳng thành đường thẳng song song hoặc trùng với nó.
Lấy điểm \(A,B\) bất kì thuộc hai đường thẳng \(a,b\) thì phép tịnh tiến theo véc tơ \(\overrightarrow {AB} \) biến đường thẳng \(a\) thành đường thẳng \(b\).
Vì các điểm \(A,B\) là lấy bất kì nên có vô số phép tịnh tiến thỏa mãn bài toán.
Một số em có thể chọn nhầm đáp án B vì chỉ xác định được một véc tơ tịnh tiến là sai
Trong mặt phẳng với hệ tọa độ $Oxy$, cho parabol $\left( P \right)$ có phương trình $y = {x^2} - x + 1$. Thực hiện liên tiếp hai phép tịnh tiến theo các vectơ $\overrightarrow u = \left( {1; - 2} \right)$ và $\overrightarrow v = \left( {2;3} \right)$, parabol $\left( P \right)$ biến thành parabol $\left( Q \right)$ có phương trình là:
-
A.
\(y = {x^2} - 7x + 14\)
-
B.
\(y = {x^2} + 3x + 2\)
-
C.
\(y = {x^2} + 5x + 6\)
-
D.
\(y = {x^2} - 9x + 5\)
Đáp án : A
- Sử dụng tính chất của phép tịnh tiến: Hợp hai phép tịnh tiến thì được phép tịnh tiến.
- Xác định véc tơ tịnh tiến \(\overrightarrow a = \overrightarrow u + \overrightarrow v \).
- Sử dụng công thức biến đổi tọa độ của phép tịnh tiến để viết phương trình parabol \(\left( Q \right)\).
Từ giả thiết ta suy ra, $\left( Q \right)$ là ảnh của $\left( P \right)$ qua phép tịnh tiến theo vectơ $\overrightarrow a = \overrightarrow u + \overrightarrow v $.
Ta có: $\overrightarrow a = \overrightarrow u + \overrightarrow v = \left( {3;1} \right)$.
Do đó phương trình của $\left( Q \right)$ là: $y - 1 = {\left( {x - 3} \right)^2} - \left( {x - 3} \right) + 1 \Leftrightarrow y = {x^2} - 7x + 14$.
Một số em có thể sẽ chọn nhầm đáp án C vì thay nhầm \(x' = x + 3;y' = y + 1\) vào phương trình của \(\left( P \right)\) là sai.
Cho đường tròn $\left( {O;R} \right)$ và hai điểm $A,B$ phân biệt. Một điểm $M$ thay đổi trên đường tròn $\left( O \right)$. Khi đó tập hợp các điểm $N$ sao cho $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} $ là tập nào sau đây?
-
A.
Tập \(\emptyset \)
-
B.
Đường tròn tâm \(A\) bán kính \(AB\)
-
C.
Đường tròn tâm \(B\) bán kính \(R\)
-
D.
Đường tròn tâm \(I\) bán kính \(R\) với \(\overrightarrow {OI} = \overrightarrow {AB} \)
Đáp án : D
- Biến đổi $\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $.
- Sử dụng tính chất: Phép tịnh tiến biến đường tròn thành đường tròn bằng nó.
Từ giả thiết ta có:
$\overrightarrow {MN} + \overrightarrow {MA} = \overrightarrow {MB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {MB} - \overrightarrow {MA} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} $
Như thế phép tịnh tiến theo vectơ $\overrightarrow u = \overrightarrow {AB} $ biến điểm $M$ thành điểm $N$.
Vậy khi $M$ thay đổi trên đường tròn $\left( {O;R} \right)$ thì quỹ tích của $N$ là đường tròn $\left( {I;R} \right)$ với $\overrightarrow {OI} = \overrightarrow {AB} $.
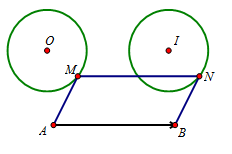
Một số em có thể sẽ chọn nhầm đáp án B vì nghĩ rằng $\overrightarrow{MN}=\overrightarrow{AB}$ nên \(N\) nằm trên đường tròn tâm \(A\) bán kính \(AB\) là sai
Ảnh $A'$ của $A\left( {4; - 3} \right)$ qua phép đối xứng trục $d$ với \(d:2x\; - y = 0\) có tọa độ là:
-
A.
$A'\left( { - 2;7} \right)$
-
B.
\(A'\left( { - \dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
-
C.
\(A'\left( {\dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
-
D.
\(A'\left( {12;\dfrac{7}{5}} \right)\)
Đáp án : B
- Viết phương trình đường thẳng $d’$ qua $A$ và vuông góc với $d.$
- Tìm giao điểm $H$ của $d$ và $d’.$ Khi đó $H$ là trung điểm của $AA’.$
Áp dụng công thức tìm tọa độ trung điểm \(\left\{ \begin{array}{l}{x_A} + {x_{A'}} = 2{x_H}\\{y_A} + {y_{A'}} = 2{y_H}\end{array} \right.\)
Gọi \(A'\) là ảnh của $A$ qua phép đối xứng trục $d.$ Gọi $d’$ là đường thẳng đi qua $A $ và vuông góc với $d,$ khi đó phương trình $d’$ có dạng: $x + 2y + c = 0.$
Vì \(A \in d'\) nên \(4 + 2\left( { - 3} \right) + c = 0 \Rightarrow c = 2\). Khi đó \(\left( {d'} \right):x + 2y + 2 = 0\)
Gọi \(H = d \cap d' \Rightarrow H\left( { - \dfrac{2}{5}; - \dfrac{4}{5}} \right) \Rightarrow \) $H $ là trung điểm của $AA’.$ Khi đó
\(\left\{ \begin{array}{l}{x_{A'}} = 2{x_H} - {x_A}\\{y_{A'}} = 2{y_H} - {y_A}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{A'}} = 2.\left( { - \dfrac{2}{5}} \right) - 4 = - \dfrac{{24}}{5}\\{y_{A'}} = 2\left( { - \dfrac{4}{5}} \right) + 3 = \dfrac{7}{5}\end{array} \right. \Rightarrow A'\left( { - \dfrac{{24}}{5};\dfrac{7}{5}} \right)\)
Hình nào sau đây có nhiều trục đối xứng nhất ?
-
A.
Hình thoi
-
B.
Hình vuông
-
C.
Hình elip
-
D.
hình tròn.
Đáp án : D
Liệt kê các trục đối xứng của từng hình.
Hình thoi có $2$ trục đối xứng (hai đường chéo).
Hình vuông có $4$ trục đối xứng (hai đường chéo và hai đường thẳng đi qua trung điểm các cạnh đối).
Elip có $2$ trục đối xứng (hai trục của Elip)
Hình tròn có vô số trục đối xứng là các đường thẳng đi qua tâm (đường kính).
Trong mặt phẳng tọa độ \(Oxy\) cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\). Phép đối xứng trục \(Ox\) biến đường tròn \(\left( C \right)\) thành đường tròn \(\left( {C'} \right)\) có phương trình là:
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4.\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 4.\)
Đáp án : C
- Tìm tâm và bán kính đường tròn đã cho.
- Xác định ảnh của tâm đường tròn qua phép đối xứng.
- Viết phương trình đường tròn ảnh và kết luận.
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 2} \right)\) và bán kính \(R = 2.\)
Ta có \(I\left( {1; - 2} \right) \Rightarrow I'\left( {1;2} \right)\) đối xứng với \(I\) qua \(Ox\) và \(R = 2 \Rightarrow R' = R = 2.\)
Do đó \(\left( {C'} \right)\) có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4.\)
Cách 2. Biểu thức tọa độ qua phép đối xứng trục \(Ox\) là \(\left\{ \begin{array}{l}x' = x\\y' = - y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = x'\\y = - y'\end{array} \right..\)
Thay vào \(\left( C \right)\), ta được \({\left( {x' - 1} \right)^2} + {\left( { - y' + 2} \right)^2} = 4\) hay \({\left( {x' - 1} \right)^2} + {\left( {y' - 2} \right)^2} = 4.\)
Khẳng định nào sau đây sai ?
-
A.
Phép đối xứng trục biến một vector thành một vector bằng nó
-
B.
Phép đối xứng trục biến một đoạn thẳng thành một đoạn thẳng bằng nó
-
C.
Phép đối xứng trục biến một tam giác thành một tam giác bằng nó
-
D.
Phép đối xứng trục biến một đường tròn thành một đường tròn có bán kính bằng với bán kính của nó.
Đáp án : A
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.
Phép đối xứng trục không bảo toàn hướng của vector.
Cho hai đường thẳng $a$ và $b$ cắt nhau tại điểm $O$. Nhận định nào sau đây là đúng?
-
A.
Không có phép đối xứng trục nào biến $a$ thành $b$
-
B.
Có duy nhất một phép đối xứng trục biến $a$ thành $b$
-
C.
Có đúng hai phép đối xứng trục biến $a$ thành $b$
-
D.
Có vô số phép đối xứng trục biến $a$ thành $b$ .
Đáp án : C
Kẻ các đường phân giác của góc tạo bởi hai đường thẳng $a$ và $b$ .
Gọi $p$ và $q$ là phân giác của các góc tạo bởi hai đường thẳng $a$ và $b$ . Ta thấy ngay có hai phép đối xứng trục biến $a$ thành $b$ là các phép đối xứng trục ${D_p}$ và ${D_q}$.
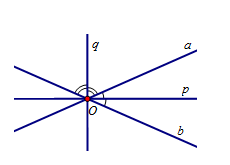
Điểm nào là ảnh của \(M\left( {3; - 1} \right)\) qua phép đối xứng tâm \(I\left( {1;2} \right)\)
-
A.
\(\left( {2;1} \right)\)
-
B.
\(\left( { - 1;5} \right)\)
-
C.
\(\left( { - 1;3} \right)\)
-
D.
\(\left( {5; - 4} \right)\)
Đáp án : B
Gọi $M'$ là điểm đối xứng với $M$ qua tâm \(I \Rightarrow I\) là trung điểm của $MM'$.
Gọi $M'$ là điểm đối xứng với $M$ qua tâm \(I \Rightarrow I\) là trung điểm của $MM'$ .
\( \Rightarrow \left\{ \begin{array}{l}{x_{M'}} = 2{x_I} - {x_M} = - 1\\{y_{M'}} = 2{y_I} - {y_M} = 5\end{array} \right. \Rightarrow M'\left( { - 1;5} \right)\)
Trong mặt phẳng tọa độ $Oxy$, nếu phép đối xứng tâm biến điểm \(A\left( {5;2} \right)\) thành điểm \(A'\left( { - 3;4} \right)\) thì nó biến điểm \(B\left( {1; - 1} \right)\) thành điểm :
-
A.
\(B'\left( {1;7} \right)\)
-
B.
\(B'\left( {1;6} \right)\)
-
C.
\(B'\left( {2;5} \right)\)
-
D.
\(B'\left( {1; - 5} \right)\)
Đáp án : A
\({D_I}\left( M \right) = M' \Rightarrow I\) là trung điểm của $MM'$
\({D_I}\left( A \right) = A' \Rightarrow I\) là trung điểm của \(AA' \Rightarrow I\left( {1;3} \right)\)
\({D_I}\left( B \right) = B' \Rightarrow I\) là trung điểm của \(BB' \Rightarrow B'\left( {1;7} \right)\)
Cho hai đường thẳng cắt nhau $d$ và $d'$. Có bao nhiêu phép đối xứng tâm biến mỗi đường thẳng đó thành chính nó
-
A.
Không có phép nào
-
B.
Có một phép duy nhất
-
C.
Chỉ có hai phép
-
D.
Có vô số phép.
Đáp án : B
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.
Qua một phép đối xứng tâm, đường thẳng biến thành chính nó khi và chỉ khi tâm đối xứng là điểm thuộc đường thẳng nó.
Gọi $O$ là tâm đối xứng sao cho qua phép đối xứng tâm $O$ biến mỗi đường thẳng $d$ và $d'$ thành chính nó.
\( \Rightarrow \left\{ \begin{array}{l}O \in d\\O \in d'\end{array} \right. \Rightarrow O = d \cap d'\) và $O$ là duy nhất.
Cho hai khẳng định sau:
(I) Nếu một hình nào đó có hai trục đối xứng vuông góc với nhau thì hình đó có tâm đối xứng.
(II) Cho phép đối xứng tâm ${D_O}$ và đường thẳng $d$ không đi qua $O$. Có thể dựng $d'$ là ảnh của $d$ qua ${D_O}$ mà chỉ sử dụng compa một lần và thước hai lần.
Chọn kết luận đúng:
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
Cả hai đều đúng
-
D.
Cả hai đều sai
Đáp án : C
Suy luận từng đáp án.
(I) đúng, tâm đối xứng của hình đó chính là giao điểm của hai trục đối xứng.
(II) Cách dựng đường thẳng $d'$ là ảnh của $d$ qua phép đối xứng tâm $O$.
Bước 1: Lấy một điểm $M$ bất kì thuộc $d$
Bước 2: Vẽ đường tròn tâm $O$ bán kính $OM$.
Bước 3: Kéo dài $OM$, cắt đường tròn tâm $O$ bán kính $OM$ tại điểm thứ hai $N$ .
Bước 4: Qua $N$ kẻ đường thẳng song song với $d$.
Vậy ta cần dùng compa ở bước 2 và dùng thước ở bước 3 và 4.
Do đó cả (I) và (II) đều đúng.
Trong mặt phẳng $Oxy$ cho hai đường thẳng \(a:\,\,2x + y + 5 = 0\) và \(b:\,\,x - 2y - 3 = 0\). Nếu có một phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc đó có thể là góc nào trong các góc cho dưới đây:
-
A.
\({45^0}\)
-
B.
\({90^0}\)
-
C.
\({120^0}\)
-
D.
\({60^0}\)
Đáp án : B
Xét mối quan hệ giữa hai đường thẳng $a$ và $b$.
Ta có: \({\overrightarrow n _a} = \left( {2;1} \right),{\overrightarrow n _b} = \left( {1; - 2} \right) \Rightarrow {\overrightarrow n _a}.{\overrightarrow n _b} = 0 \Rightarrow a \bot b\)
Do đó tồn tại phép quay góc \({90^0}\) biến đường thẳng này thành đường thẳng kia
Trong mặt phẳng tọa độ $Oxy$ cho phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\). Khi đó nó biến điểm \(M\left( {1; - 1} \right)\) thành điểm:
-
A.
\(M'\left( { - 1; - 1} \right)\)
-
B.
\(M'\left( {1;1} \right)\)
-
C.
\(M'\left( { - 1;1} \right)\)
-
D.
\(M'\left( {1;0} \right)\)
Đáp án : B
Xác định góc quay.
Áp dụng công thức tính tọa độ ảnh của điểm \(M\left( {x;y} \right)\) qua phép quay tâm $O$ góc \(\alpha :\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Phép quay tâm $O$ biến điểm \(A\left( {1;0} \right)\) thành điểm \(A'\left( {0;1} \right)\) là phép quay tâm $O$ góc \({90^0}\)
Gọi \(M'\left( {x';y'} \right)\) là ảnh của điểm \(M\left( {1; - 1} \right)\) qua phép quay tâm $O$ góc \({90^0}\) ta có: \(\left\{ \begin{array}{l}x' = 1.\cos {90^0} + 1.\sin {90^0}\\y' = 1.\sin {90^0} - 1.\cos {90^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x' = 1\\y' = 1\end{array} \right. \Rightarrow M'\left( {1;1} \right)\)
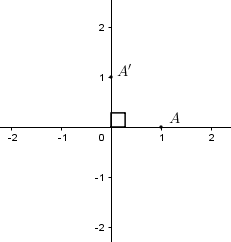
Trong mặt phẳng $Oxy$ cho đường thẳng \(d:\,\,x - y + 4 = 0\). Hỏi trong $4$ đường thẳng cho bởi các phương trình sau, đường thẳng nào có thể biến thành $d$ qua phép quay tâm \(I\left( {0;3} \right)\) góc quay \(\pi \) ?
-
A.
\(2x + y - 4 = 0\)
-
B.
\(2x + 2y - 3 = 0\)
-
C.
\(x - y + 2 = 0\)
-
D.
\(2x - 2y + 1 = 0\)
Đáp án : C
Gọi đường thẳng cần tìm là \(\Delta \), ta có: \({Q_{\left( {I;\pi } \right)}}:\,\,\Delta \,\, \mapsto \,\,d \Rightarrow {Q_{\left( {I; - \pi } \right)}}:\,\,d\,\, \mapsto \,\,\Delta \)
Ta lấy hai điểm bất kì thuộc $d$ và tìm ảnh của hai điểm đó qua phép quay \(Q\left( {I; - \pi } \right)\) sau đó viết phương trình đường thẳng đi qua hai ảnh vừa tìm được, đó chính là đường thẳng cần tìm.
Gọi đường thẳng cần tìm là \(\Delta \), ta có: \({Q_{\left( {I;\pi } \right)}}:\,\,\Delta \,\, \mapsto \,\,d \Rightarrow {Q_{\left( {I; - \pi } \right)}}:\,\,d\,\, \mapsto \,\,\Delta \)
Ta lấy hai điểm bất kì thuộc $d$ và tìm ảnh của hai điểm đó qua phép quay \(Q\left( {I; - \pi } \right)\)
Lấy \(A\left( {0;4} \right);B\left( { - 4;0} \right) \in d\)
Gọi \(A',B'\) lần lượt là ảnh của $A$ và $B$ qua phép quay \(Q\left( {I; - \pi } \right)\)
Ta có: \(\left\{ \begin{array}{l}IA = IA'\\\widehat {AIA'} = - {180^0}\end{array} \right. \Rightarrow \) I là trung điểm của \(AA' \Rightarrow A'\left( {0;2} \right)\)
Tương tự ta có $I$ là trung điểm của \(BB' \Rightarrow B'\left( {4;6} \right)\)
Vậy phương trình đường thẳng \(\Delta \) đi qua $A$ và $B$ là : \(\dfrac{{x - 0}}{{4 - 0}} = \dfrac{{y - 2}}{{6 - 2}} \Leftrightarrow \dfrac{x}{4} = \dfrac{{y - 2}}{4} \Leftrightarrow x - y + 2 = 0\)
\({Q_{\left( {I;\pi } \right)}}\) và \({Q_{\left( {I; - \pi } \right)}}\) chính là phép đối xứng tâm $I$.
Khẳng định nào sai ?
-
A.
Phép tịnh tiến một đoạn thẳng thành một đoạn thẳng bằng nó
-
B.
Phép quay biến đường thẳng thành đường thẳng song song với nó
-
C.
Phép tịnh tiến biến tam giác thành tam giác bằng nó.
-
D.
Phép quay biến đường tròn thành đường tròn có cùng bán kính.
Đáp án : B
Dựa vào định nghĩa phép dời hình: Phép dời hình là phép bảo toàn khoảng cách giữa hai điểm bất kì.
Phép quay và phép tịnh tiến đều là phép dời hình, do đó các đáp án A, C, D đúng.
Đáp án B sai vì phép quay có góc quay $90^0$ biến đường thẳng thành đường thẳng vuông góc với nó.
Trong mặt phẳng $Oxy$ cho điểm \(M\left( { - 2;4} \right)\). Phép vị tự tâm $O$ tỉ số \(k = - 2\) biến điểm $M$ thành điểm nào trong các điểm sau?
-
A.
\(\left( { - 3;4} \right)\)
-
B.
\(\left( { - 4; - 8} \right)\)
-
C.
\(\left( {4; - 8} \right)\)
-
D.
\(\left( {4;8} \right)\)
Đáp án : C
\({V_{\left( {O;k} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'} = k\overrightarrow {OM} \)
Gọi điểm \(M'\left( {x';y'} \right)\) là ảnh của điểm $M$ qua phép vị tự tâm $O$ tỉ số \(k = - 2\).
\({V_{\left( {O; - 2} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {OM'} = - 2\overrightarrow {OM} \Leftrightarrow \left( {x';y'} \right) = - 2\left( { - 2;4} \right) \Leftrightarrow \left\{ \begin{array}{l}x' = 4\\y' = - 8\end{array} \right. \Rightarrow M\left( {4; - 8} \right)\)
Trong mặt phẳng tọa độ \(Oxy\) cho phép vị tự \(V\) tỉ số \(k = 2\) biến điểm \(A\left( {1; - 2} \right)\) thành điểm \(A'\left( { - 5;1} \right).\) Hỏi phép vị tự \(V\) biến điểm \(B\left( {0;1} \right)\) thành điểm có tọa độ nào sau đây?
-
A.
\(\left( {0;2} \right).\)
-
B.
\(\left( {12; - 5} \right).\)
-
C.
\(\left( { - 7;7} \right).\)
-
D.
\(\left( {11;6} \right).\)
Đáp án : C
Sử dụng tính chất của phép vị tự \({V_{\left( {I;k} \right)}}\left( A \right) = A',{V_{\left( {I;k} \right)}}\left( B \right) = B'\) \( \Leftrightarrow \overrightarrow {A'B'} = k\overrightarrow {AB} \)
Gọi \(B'\left( {x;y} \right)\) là ảnh của \(B\) qua phép vị tự \(V.\)
Suy ra \(\overrightarrow {A'B'} = \left( {x + 5;y - 1} \right)\) và \(\overrightarrow {AB} = \left( { - 1;3} \right).\)
Theo giả thiết, ta có \(\overrightarrow {A'B'} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}x + 5 = 2.\left( { - 1} \right)\\y - 1 = 2.3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 7\\y = 7\end{array} \right.\).
Trong mặt phẳng tọa độ $Oxy$. Cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt có phương trình \(x - 2y + 1 = 0\) và \(x - 2y + 4 = 0\), điểm \(I\left( {2;1} \right)\). Phép vị tự tâm $I$ tỉ số $k$ biến đường thẳng \({\Delta _1}\) thành \({\Delta _2}\) khi đó giá trị của $k$ là :
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Đáp án : D
Lấy điểm $A$ bất kì thuộc \({\Delta _1}\), tìm ảnh $A'$ của $A$ qua phép vị tự tâm $I$ tỉ số $k$.
Thay tọa độ điểm $A'$ vừa tìm được vào phương trình đường thẳng \({\Delta _2}\).
Lấy \(A\left( { - 1;0} \right) \in {\Delta _1}\), gọi \(A'\left( {x;y} \right)\) là ảnh của $A$ qua phép vị tự tâm $I$ tỉ số $k$ ta có : \(\overrightarrow {IA'} = k\overrightarrow {IA} \)
\(\begin{array}{l} \Rightarrow \left( {x - 2;y - 1} \right) = k\left( { - 3; - 1} \right) \Leftrightarrow \left\{ \begin{array}{l}x - 2 = - 3k\\y - 1 = - k\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - 3k + 2\\y = - k + 1\end{array} \right. \Rightarrow A'\left( { - 3k + 2; - k + 1} \right)\\{V_{\left( {I;k} \right)}}\left( {{\Delta _1}} \right) = {\Delta _2},\,\,{V_{\left( {I;k} \right)}}\left( A \right) = A' \Rightarrow A' \in {\Delta _2}\end{array}\)
Thay tọa độ điểm $A'$ vào phương trình đường thẳng \({\Delta _2}\) ta có:
\( - 3k + 2 - 2\left( { - k + 1} \right) + 4 = 0 \Leftrightarrow - k + 4 = 0 \Leftrightarrow k = 4\)
Cho tam giác $ABC$ có trực tâm $H$, trọng tâm $G$ và tâm đường tròn ngoại tiếp $O$ . Phép vị tự tâm $G$ biến $H$ thành $O$ có tỉ số là :
-
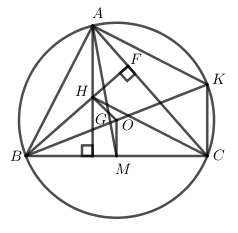
A.
$2$
-
B.
\(\dfrac{1}{2}\)
-
C.
\( - \dfrac{1}{2}\)
-
D.
\( - \dfrac{2}{3}\)
Đáp án : C
Chứng minh $H,G,O$ thẳng hàng mà tìm mối tỉ số \(\dfrac{{GO}}{{GH}}\)
Gọi $H$ và $O$ lần lượt là trực tâm và tam đường tròn ngoại tiếp tâm giác $ABC$ .
Gọi $M$ là trung điểm của $BC$ , kẻ đường kính $BK$.
Xét đường tròn ngoại tiếp tâm $O$ có \(\widehat {BCK}\) nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {BCK} = {90^0} \Rightarrow BC \bot CK\)
Mà \(AH \bot BC \Rightarrow AH//CK\)
Tương tự ta chứng minh được \(AK//CH\)
\( \Rightarrow \) Tứ giác $AHCK$ là hình bình hành \( \Rightarrow AH = CK\)
Có $OM$ là đường trung bình của tam giác \(BCK \Rightarrow OM//CK//AH\) và \(OM = \dfrac{1}{2}CK = \dfrac{1}{2}AH\).
Gọi \(G = AM \cap OH\) ta dễ thấy \(\Delta AGH \sim \Delta MGO\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{AG}}{{MG}} = \dfrac{{AH}}{{OM}} = 2 = \dfrac{{HG}}{{OG}}\) , mà $AM$ là trung tuyến của tam giác \(ABC \Rightarrow G\) là trọng tâm tam giác $ABC$ . Vậy $H,G,O$ thẳng hàng, với $G$ là trọng tâm tam giác $ABC$ và \(\dfrac{{HG}}{{OG}} = 2 \Rightarrow \overrightarrow {GO} = - \dfrac{1}{2}\overrightarrow {GH} \)
\( \Rightarrow {V_{\left( {G; - \frac{1}{2}} \right)}}\left( H \right) = O\).
Mệnh đề nào sau đây là đúng?
-
A.
Phép đồng dạng tỉ số \(k = 1\) là phép dời hình.
-
B.
Phép đồng dạng tỉ số \(k = - 1\) là phép đối xứng tâm.
-
C.
Phép đồng dạng tỉ số \(k = 1\) là phép tịnh tiến
-
D.
Phép đồng dạng tỉ số \(k = 1\) là phép vị tự tỉ số \(k = 1\)
Đáp án : A
Khi \(k = 1\) phép đồng dạng bảo toàn khoảng cách nên là phép dời hình.
Một số em có thể sẽ chọn nhầm đáp án D là sai vì phép đồng dạng tỉ số \(k = 1\) cũng có thể là phép vị tự tỉ số \(k = - 1\).
Cho $\Delta ABC$ đều cạnh $2$. Qua ba phép đồng dạng liên tiếp: Phép tịnh tiến ${T_{\overrightarrow {BC} }}$, phép quay $Q\left( {B,{{60}^0}} \right)$, phép vị tự ${V_{\left( {A,\,3} \right)}},\Delta ABC$ biến thành $\Delta {A_1}{B_1}{C_1}$. Diện tích $\Delta {A_1}{B_1}{C_1}$ là:
-
A.
$5\sqrt 2 $
-
B.
$9\sqrt 3 $
-
C.
$9\sqrt 2 $
-
D.
$5\sqrt 3 $
Đáp án : B
- Sử dụng tính chất phép tịnh tiến, phép quay biến tam giác thành tam giác bằng nó.
- Sử dụng tính chất phép vị tự biến tam giác thành tam giác đồng dạng.
Do phép tịnh tiến và phép quay bảo toàn khoảng cách giữa các cạnh nên phép tịnh tiến ${T_{\overrightarrow {BC} }}$, phép quay $Q\left( {B,{{60}^0}} \right)$, phép vị tự ${V_{\left( {A,3} \right)}},\Delta ABC$ biến thành $\Delta {A_1}{B_1}{C_1}$ thì \({A_1}{B_1} = 3AB = 6\)
Tam giác đều $\Delta {A_1}{B_1}{C_1}$ có cạnh bằng $6 \Rightarrow {S_{\Delta {A_1}{B_1}{C_1}}} = \dfrac{{{6^2}\sqrt 3 }}{4} = 9\sqrt 3 $.
Một số em có thể sẽ chọn nhầm đáp án C vì nhớ nhầm công thức tính diện tích tam giác đều.
Trong mặt phẳng \(Oxy,\) cho đường thẳng \(d:2x - y = 0\). Phương trình đường thẳng qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm \(O\) tỉ số \(k = - 2\) và phép đối xứng trục \(Oy\) là đường thẳng nào sau đây?
-
A.
\( -2x - y = 0\).
-
B.
\(2x - y = 0\).
-
C.
\(4x - y = 0\).
-
D.
\(2x + y - 2 = 0\)
Đáp án : A
- Sử dụng tính chất: Phép vị tự biến đường thẳng thành đường thẳng song song (hoặc trùng) với đường thẳng đó.
Tìm ảnh của đường thẳng \(d: ax+by+c=0\) qua phép vị tự:
B1: Gọi phương trình đường thẳng của ảnh \(d'\) là \(ax+by+c+m=0\)
B2: Lấy một điểm \(M\) thuộc \(d\), tìm ảnh \(M'\) của nó qua phép vị tự rồi thay \(M'\) vào phương trình của \(d'\) để tìm tham số \(m\).
- Sử dụng biểu thức tọa độ của phép đối xứng qua hai trục tọa độ: đối xứng qua cái gì thì giữ nguyên cái đó, còn lại lấy giá trị đối.
Ta có: \({V_{\left( {O; - 2} \right)}}\left( d \right) = d' \Rightarrow d'//d\) hoặc \(d' \equiv d\).
\( \Rightarrow d'\) có dạng: \(2x - y + m = 0\)
Chọn \(N\left( {1;2} \right) \in d:{V_{\left( {O; - 2} \right)}}\left( N \right) = N'\left( { - 2; - 4} \right) \in d' \Rightarrow - 4 + 4 + m = 0 \Rightarrow m = 0\)
\( \Rightarrow \) Phương trình đường thẳng \(d':2x - y = 0\)
Qua phép đối xứng trục \(Oy\): \({D_{oy}}\left( {d'} \right) = d''\)
\(\begin{array}{*{20}{l}}\begin{array}{l}M(x,y) \in d'\\ \Rightarrow {D_{Oy}}(M) = M'(x',y') \in d''\end{array}\\\begin{array}{l} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x' = - x}\\{y' = y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - x'}\\{y = y'}\end{array}} \right.\\ \Rightarrow 2( - x') - y' = 0\end{array}\end{array}\)
Suy ra phương trình ảnh \(d''\) cần tìm là: \( - 2x - y = 0\)
Có thể nhận xét nhanh rằng, tâm \(O \in d\) nên phép vị tự tâm \(O\) sẽ biến đường thẳng \(d\) thành chính nó.
Cho phương trình \(\sin \left( {2x - \dfrac{\pi }{5}} \right) = 3{m^2} + \dfrac{m}{2}\). Biết \(x = \dfrac{{11\pi }}{{60}}\) là một nghiệm của phương trình. Tính \(m\).
-
A.
\(\left[ \begin{array}{l}m = 1\\m = \dfrac{1}{2}\end{array} \right.\)
-
B.
\(\left[ \begin{array}{l}m = - \dfrac{3}{2}\\m = 0\end{array} \right.\)
-
C.
\(\left[ \begin{array}{l}m = - \dfrac{1}{4}\\m = \dfrac{2}{3}\end{array} \right.\)
-
D.
\(\left[ \begin{array}{l}m = - \dfrac{1}{2}\\m = \dfrac{1}{3}\end{array} \right.\)
Đáp án : D
Thay \(x = \dfrac{{11\pi }}{{60}}\) sau đó giải phương trình tìm \(m\).
Thay \(x = \dfrac{{11\pi }}{{60}}\) vào phương trình ta có:
\(\begin{array}{l}\sin \left( {2.\dfrac{{11\pi }}{{60}} - \dfrac{\pi }{5}} \right) = 3{m^2} + \dfrac{m}{2} \Leftrightarrow \sin \dfrac{\pi }{6} = 3{m^2} + \dfrac{m}{2}\\ \Leftrightarrow \dfrac{1}{2} = 3{m^2} + \dfrac{m}{2} \Leftrightarrow 6{m^2} + m = 1 \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{3}\\m = - \dfrac{1}{2}\end{array} \right.\end{array}\)
Giải phương trình \(\cos 2x + \cos 4x + \cos 6x = \cos x\cos 2x\cos 3x + 2\).
-
A.
\(x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
B.
\(x = \dfrac{2\pi }{{3}} + 2k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
C.
\(x =\dfrac{{\pi }}{3} + 2k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
-
D.
\(x = \dfrac{k\pi }{{3}} \,\,\left( {k \in \mathbb{Z}} \right)\).
Đáp án : A
- Sử dụng công thức biến đổi tích thành tổng: \(\cos a\cos b = \dfrac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\).
- Sử dụng công thức nhân đôi: \(\cos 2\alpha = 2{\cos ^2}\alpha - 1\).
- Đưa phương trình về dạng phương trình bậc ba đối với 1 hàm số lượng giác.
\(\begin{array}{l}\,\,\,\,\,\,\cos 2x + \cos 4x + \cos 6x = \cos x\cos 2x\cos 3x + 2\\ \Leftrightarrow 2\cos 4x\cos 2x + \cos 4x = \dfrac{1}{2}\cos 2x\left( {\cos 4x + \cos 2x} \right) + 2\\ \Leftrightarrow 2\cos 4x\cos 2x + \cos 4x = \dfrac{1}{2}\cos 2x\cos 4x + \dfrac{1}{2}{\cos ^2}2x + 2\\ \Leftrightarrow \dfrac{3}{2}\cos 4x\cos 2x + \cos 4x = \dfrac{1}{2}{\cos ^2}2x + 2\\ \Leftrightarrow 3\cos 4x\cos 2x + 2\cos 4x = {\cos ^2}2x + 4\\ \Leftrightarrow 3\left( {2{{\cos }^2}2x - 1} \right)\cos 2x + 2\left( {2{{\cos }^2}2x - 1} \right) = {\cos ^2}2x + 4\\ \Leftrightarrow 6{\cos ^3}2x - 3\cos 2x + 4{\cos ^2}2x - 2 = {\cos ^2}2x + 4\\ \Leftrightarrow 6{\cos ^3}2x + 3{\cos ^2}2x - 3\cos 2x - 6 = 0\\ \Leftrightarrow 2{\cos ^3}2x + {\cos ^2}2x - \cos 2x - 2 = 0\\ \Leftrightarrow 2\left( {{{\cos }^3}2x - 1} \right) + \cos 2x\left( {\cos 2x - 1} \right) = 0\\ \Leftrightarrow 2\left( {\cos 2x - 1} \right)\left( {{{\cos }^2}2x + \cos 2x + 1} \right) + \cos 2x\left( {\cos 2x - 1} \right) = 0\\ \Leftrightarrow \left( {\cos 2x - 1} \right)\left( {2{{\cos }^2}2x + 2\cos 2x + 2 + \cos 2x} \right) = 0\\ \Leftrightarrow \left( {\cos 2x - 1} \right)\left( {2{{\cos }^2}2x + 3\cos 2x + 2} \right) = 0\\ \Leftrightarrow \cos 2x = 1 \Leftrightarrow 2x = k2\pi \Leftrightarrow x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy nghiệm của phương trình đã cho là: \(x = k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Có bao nhiêu cách xếp \(5\) học sinh thành một hàng dọc?
-
A.
\(1\).
-
B.
\(25\).
-
C.
\(5\).
-
D.
\(120\).
Đáp án : D
Số cách sắp xếp \(n\) bạn vào \(n\) vị trí khác nhau là \({P_n} = n!\)
Mỗi cách xếp cho ta một hoán vị của 5 học sinh và ngược lại.
Vậy số cách xếp là \({P_5} = 5! = 120\) (cách).
Số (5! – P4) bằng:
-
A.
5
-
B.
12
-
C.
24
-
D.
96
Đáp án : D
\(5! - {P_4} = 5! - 4! = 96\).
Cho hình bình hành ABCD. Phép tịnh tiến theo \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\) biến đoạn thẳng DC thành đoạn thẳng nào sau đây?
-
A.
BC
-
B.
AB
-
C.
DC
-
D.
CA
Đáp án : B
Sử dụng định nghĩa phép tịnh tiến: \({T_{\overrightarrow u }}\left( A \right) = B \Rightarrow \overrightarrow {AB} = \overrightarrow u \).
Ta có: \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \).
Mà ABCD là hình bình hành nên \(\overrightarrow {CB} = \overrightarrow {DA} \).
Do đó
\(\begin{array}{l}{T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( D \right) = {T_{\overrightarrow {CB} }}\left( D \right) = A\\{T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( C \right) = {T_{\overrightarrow {CB} }}\left( C \right) = B\end{array}\)
Vậy \({T_{\overrightarrow {AB} - \overrightarrow {AC} }}\left( {DC} \right) = {T_{\overrightarrow {CB} }}\left( {DC} \right) = AB\)
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2










Danh sách bình luận