Trên mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C(-1;0). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC.
-
A.
(0;0)
-
B.
(1;0)
-
C.
(2;0)
-
D.
(3;0)
- Viết phương trình đường thẳng \(BC\), tham số hóa tọa độ điểm \(M \in BC\) theo tham số \(m\).
- Viết phương trình đường thẳng \(AM\) theo \(m\).
- Tính \(d\left( {B;AM} \right)\) và \(d\left( {C;AM} \right)\). Sử dụng công thức khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(ax + by + c = 0\) là \(d\left( {M;AB} \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
- Để \({S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\), giải phương trình tìm \(m\).
Phương trình đường thẳng \(BC\) là \(y = 0\), vì \(M \in BC\) nên gọi \(M\left( {m;0} \right)\).
Ta có: \(\overrightarrow {AM} = \left( {m - 2; - 3} \right)\) nên \(\overrightarrow n = \left( {3;m - 2} \right)\) là 1 VTPT của đường thẳng \(AM\).
Phương trình đường thẳng \(AM\) là:
\(\begin{array}{l}3\left( {x - 2} \right) + \left( {m - 2} \right)\left( {y - 3} \right) = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 6 - 3m + 6 = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 3m = 0\end{array}\)
\(\begin{array}{l} \Rightarrow d\left( {B;AM} \right) = \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\\,\,\,\,\,\,d\left( {C;AM} \right) = \dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\end{array}\)
Ta có: \(\left\{ \begin{array}{l}{S_{\Delta MAB}} = \dfrac{1}{2}d\left( {B;AM} \right).AM\\{S_{\Delta MAC}} = \dfrac{1}{2}d\left( {C;AM} \right).AM\end{array} \right. \Rightarrow {S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right)\).
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }} = 2\dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\ \Leftrightarrow \left| {15 - 3m} \right| = 2\left| { - 3 - 3m} \right|\\ \Leftrightarrow \left[ \begin{array}{l}15 - 3m = - 6 - 6m\\15 - 3m = 6 + 6m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 7\\m = 1\end{array} \right.\end{array}\)
Vậy \(M\left( {1;0} \right)\) hoặc \(M\left( { - 7;0} \right)\).
Đáp án : B
Các bài tập cùng chuyên đề
Tính khoảng cách từ điểm \(M\left( {1;2} \right)\) đến đường thẳng\(\Delta :\left\{ \begin{array}{l}x = 5 + 3t\\y = - 5 - 4t\end{array} \right.\).
Đo trực tiếp khoảng cách từ điểm M đến đường thẳng A(H7.10) và giải thích vì sao kết quả đo đạc đó phù hợp với kết quả tính toán trong lời giải của Ví dụ 4.
Cho điểm \(M\left( {{x_o};{y_0}} \right)\) và đường thẳng \(\Delta :{\rm{a}}x + by + c = 0\) có vecto pháp tuyến \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right)\)
Gọi H là hình chiếu vuông góc của M trên \(\Delta \).
a) Chưng minh rằng \(\left| {\overrightarrow n .\overrightarrow {HM} } \right| = \sqrt {{a^2} + {b^2}} .HM\)
b) Giả sử H có tọa độ \(\left( {{x_1};{y_1}} \right)\). Chứng minh rằng \(\overrightarrow n .\overrightarrow {HM} = a\left( {{x_o} - {x_1}} \right) + b\left( {{y_o} - {y_1}} \right) = a{x_o} + b{y_o} + c\)
c) Chứng minh rằng \(HM = \frac{{\left| {{\rm{a}}{x_o} + b{y_o} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Tính khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\).
Trong mặt phẳng Oxy, cho tam giác ABC có tọa độ các đỉnh là \(A(1;1),B(5;2),C(4;4)\). Tính độ dài các đường cao của tam giác ABC.
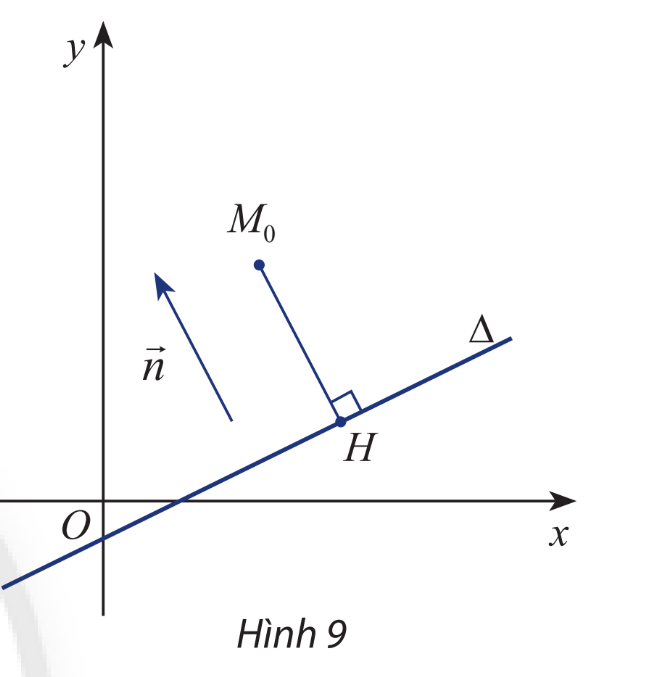
Trong mặt phẳng Oxy. Cho đường thẳng \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) có vectơ pháp tuyến \(\overrightarrow n \) và cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) có hình chiếu vuông góc \(H\left( {{x_H};{y_H}} \right)\)trên \(\Delta \)(hình 9).
a) Chứng minh rằng hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \) cùng phương và tìm tọa độ của chúng.
b) Gọi p là tích vô hướng của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \).
Chứng minh rằng \(p = a{x_0} + b{y_0} + c\).
c) Giải thích công thức \(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\).
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M(1;2)\) và \(\Delta :3x - 4y + 12 = 0\)
b) \(M(4;4)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = - t\end{array} \right.\)
c) \(M(0;5)\) và \(\Delta :\left\{ \begin{array}{l}x = t\\y = \frac{{ - 19}}{4}\end{array} \right.\)
d) \(M(0;0)\) và \(\Delta :3x + 4y - 25 = 0\)
Tính khoảng cách giữa hai đường thẳng \(\Delta :3x + 4y - 10 = 0\) và \(\Delta ':6x + 8y - 1 = 0\).
Trong mặt phẳng Oxy cho điểm \(S(x;y)\) di động trên đường thẳng \(d:12x - 5y + 16 = 0\). Tính khoảng cách ngắn nhất từ điểm \(M(5;10)\) đến điểm S.
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y - 13 = 0\) và \(\Delta ':3x + 4y - 27 = 0\).
a) Tính khoảng cách từ điểm \(O\left( {0{\rm{;}}0} \right)\) đến đường thẳng \(\Delta \):\(\frac{x}{{ - 4}} + \frac{y}{2} = 1\)
b) Tính khoảng cách giữa hai đường thẳng song song \({\Delta _1}:x - y + 1 = 0\) và \({\Delta _2}:x - y - 1 = 0\)
Tính khoảng cách từ một điểm đến một đường thẳng trong mỗi trường hợp sau:
a) \(A\left( {1; - 2} \right){\rm{ }}v\`a {\rm{ }}{\Delta _1}:{\rm{ }}3x - y + {\rm{ }}4{\rm{ }} = {\rm{ }}0\);
b) B(-3; 2) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 2 + t\\y = 1 - 2t\end{array} \right.\)
Khoảng cách từ điểm \(A\left( {1;1} \right)\) đến đường thẳng \(\Delta :3x + 4y + 13 = 0\) bằng:
A. 1
B. 2
C. 3
D. 4
Trong mặt phẳng \(Oxy\), tìm điểm M thuộc trục Ox sao cho khoảng cách từ M đến đường thẳng \(\Delta :3x + y - 3 = 0\) bằng \(\sqrt {10} \).
Cho điểm \(A\left( {2;3} \right)\) và đường thẳng \(d:x + y + 3 = 0\). Khoảng cách từ điểm A đến đường thẳng d là:
A. \(\frac{8}{{\sqrt {13} }}\)
B. \(4\sqrt 2 \)
C. 8
D. \(2\sqrt 2 \)
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M\left( {2;3} \right)\) và \(\Delta :8x - 6y + 7 = 0\).
b) \(M\left( {0;1} \right)\) và \(\Delta :4x + 9y - 20 = 0\).
c) \(M\left( {1;1} \right)\) và \(\Delta :3y - 5 = 0\).
d) \(M\left( {4;9} \right)\) và \(\Delta :x - 25 = 0\).
Tìm c để đường thẳng \(\Delta :4x - 3y + c = 0\) tiếp xúc với đường tròn \(\left( C \right)\) có \(J\left( {1;2} \right)\) và bán kính \(R = 3\).
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y - 11 = 0\) và \(\Delta ':6x + 8y - 1 = 0\).
Một trạm viễn thông \(S\) có tọa độ \(\left( {5;1} \right)\). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng \(\Delta \) có phương trình \(12x + 5y - 20 = 0\). Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông \(S\). Biết rằng mỗi đơn vị độ dài tương ứng với 1 km.
Bán kính của đường tròn tâm \(I\left( {0; - 2} \right)\) và tiếp xúc với đường thẳng \(\Delta :3x - 4y - 23 = 0\) là:
A. 15
B. 5
C. \(\frac{3}{5}\)
D. 3
Tính khoảng cách giữa hai đường thẳng \(\Delta :ax + by + c = 0\) và \(\Delta ':ax + by + d = 0\) (biết \(\Delta //\Delta '\)).
Khoảng cách từ điểm M(5;–2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:
A. 13
B. \(\sqrt {13} \)
C. \(\frac{{\sqrt {13} }}{{13}}\)
D. \(2\sqrt {13} \)
Tính khoảng cách từ một điểm đến một đường thẳng trong các trường hợp sau:
a) A(−3 ; 1) và ∆1: 2x + y - 4 = 0.
b) B(1; -3) và ∆2: \(\left\{ \begin{array}{l}x = - 3 + 3t\\y = 1 - t\end{array} \right.\).
Cho hai đường thẳng song song ∆1: ax + by + c = 0 và ∆2: ax + by + d = 0. Chứng minh rằng khoảng cách giữa hai đường thẳng ∆1 và ∆2 bằng \(\frac{{\left| {d - c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).
Khoảng cách từ điểm M(4 ; –2) đến đường thẳng ∆: x − 2y + 2 = 0 bằng:
A. \(\frac{{2\sqrt 5 }}{5}\)
B. \(2\sqrt 5 \)
C. 2
D. \(\sqrt 5 \)
Khoảng cách từ giao điểm của hai đường thẳng \(x - 3y + 4 = 0\) và \(2x + 3y - 1 = 0\) đến đường thẳng $\Delta :3x + y + 4 = 0$ bằng:
Cho đường thẳng \(\Delta :\dfrac{{x - 1}}{2} = \dfrac{{y + 3}}{{ - 1}}\) và điểm \(N\left( {1;\, - 4} \right)\). Khoảng cách từ điểm \(N\) đến đường thẳng \(\Delta \) bằng
Khoảng cách từ điểm M(–2;2) đến đường thẳng Δ: \(5x - 12y + 8 = 0\) bằng
Lập phương trình đường thẳng \(\Delta\) đi qua M(2;7) và cách N(1;2) một khoảng bằng 1.
Cho hai đường thẳng song ${d_1}:5x - 7y + 4 = 0\,\,$và ${d_2}:5x - 7y + 6 = 0.\,\,$Khoảng cách giữa \({d_1}\) và \({d_2}\) là
