Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Ôn tập chương III - Phương trình. Hệ phương trình
Bài 9 trang 71 SGK Đại số 10
Hỏi nếu vẫn tiếp tục làm việc với năng suất đó thì khi đến hạn phân xưởng làm được tất cả bao nhiêu sản phẩm.
Đề bài
Một phân xưởng được giao sản xuất \(360\) sản phẩm trong một số ngày nhất định. Vì phân xưởng tăng năng suất, mỗi ngày làm thêm được \(9\) sản phẩm so với định mức trên, nên trước khi hết hạn một ngày thì phân xưởng đã làm vượt số sản phẩm được giao là \(5\%\). Hỏi nếu vẫn tiếp tục làm việc với năng suất đó thì khi đến hạn phân xưởng làm được tất cả bao nhiêu sản phẩm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Giải bài toán bằng cách lập phương trình:
+) Gọi ẩn và đặt điều kiện cho ẩn.
+) Biểu diện các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+) Dựa vào đề bài lập phương trình.
+) Giải phương trình tìm ẩn.
+) Đối chiếu với điều kiện của ẩn và kết luận nghiệm.
Lời giải chi tiết
Gọi \(x\) là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện \(x > 0,x \in \mathbb {N}\).
Phân xưởng được giao sản xuất \(360\) sản phẩm nên số ngày hoàn thành theo dự định là \({{360} \over x}\) ngày
Phân xưởng tăng năng suất, mỗi ngày làm thêm được \(9\) sản phẩm so với định mức nên mỗi ngày xưởng làm được \(x+9\) sản phẩm.
Trước khi hết hạn một ngày thì phân xưởng đã làm vượt số sản phẩm được giao là \(5\%\) nên số sản phẩm làm được là: 360+360.5%=378 sản phẩm.
Số ngày làm 378 sản phẩm là \(\frac{{360}}{x} - 1\).
Lại có, mỗi ngày làm được x+9 sản phẩm, trong \(\frac{{360}}{x} - 1\) ngày làm được 378 sản phẩm
Nên ta có phương trình:
\(\begin{array}{l}
\left( {\frac{{360}}{x} - 1} \right).\left( {x + 9} \right) = 378\\
\Leftrightarrow \frac{{360 - x}}{x}.\left( {x + 9} \right) = 378\\
\Leftrightarrow \frac{{\left( {360 - x} \right)\left( {x + 9} \right)}}{x} = 378\\
\Rightarrow \left( {360 - x} \right)\left( {x + 9} \right) = 378x\\
\Leftrightarrow - {x^2} + 351x + 3240 - 378x = 0\\
\Leftrightarrow - {x^2} - 27x + 3240 = 0
\end{array}\)
\(\Leftrightarrow \left[ \matrix{
x = - 72\text{ ( loại ) } \hfill \cr
x = 45\text{ ( thỏa mãn ) } \hfill \cr} \right.\)
Thời gian giao hoàn thành kế hoạch là \({{360} \over {45}} = 8\) ngày.
Năng suất thực tế là 45+9=54 sản phẩm/ngày
Vậy nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là \(54.8=432\) sản phẩm.
Cách khác:
Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
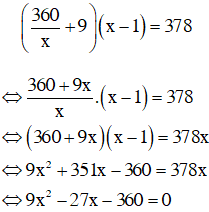
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 71 SGK Đại số 10
- Bài 11 trang 71 SGK Đại số 10
- Bài 12 trang 71 SGK Đại số 10
- Bài 13 trang 71 SGK Đại số 10
- Bài 14 trang 71 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
