 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 4. Tính chất ba đường trung tuyến của tam giác
Bài 4. Tính chất ba đường trung tuyến của tam giác
Bài 28 trang 67 SGK Toán 7 tập 2
Cho tam giác DEF cân tại D với đường trung tuyến DI
Đề bài
Cho tam giác \(DEF\) cân tại \(D\) với đường trung tuyến \(DI\).
a) Chứng minh \(∆DEI = ∆DFI.\)
b) Các góc \(DIE\) và góc \(DIF\) là những góc gì?
c) Biết \(DE = DF = 13\,cm,\) \(EF = 10\,cm,\) hãy tính độ dài đường trung tuyến \(DI.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của tam giác cân, tính chất đường trung tuyến và định lý Pytago.
Lời giải chi tiết
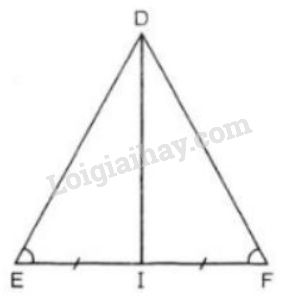
a) Cách 1:
Xét \(∆DEI\) và \(∆DFI\) có:
+) \(DE = DF\) (vì \( ∆DEF\) cân tại \(D\))
+) \(\widehat{DEI}=\widehat{DFI}\) (vì \( ∆DEF\) cân tại \(D\))
+) \(IE = IF\) ( vì \(DI\) là trung tuyến)
Vậy \(∆DEI = ∆DFI\) (c.g.c)
Cách 2:
Xét \(∆DEI\) và \(∆DFI\) có:
+) \(DI\) là cạnh chung
+) \(DE = DF\) (vì \( ∆DEF\) cân tại \(D\))
+) \(IE = IF\) ( vì \(DI\) là trung tuyến)
Vậy \(∆DEI = ∆DFI\) (c.c.c)
b) Vì \(∆DEI = ∆DFI\) (theo câu a) nên \(\widehat{DIE} =\widehat{DIF}\) ( 2 góc tương ứng)
Mà \(\widehat{DIE} +\widehat{DIF} = 180^o\) ( hai góc kề bù)
\(\Rightarrow \) \(\widehat{DIE} =\widehat{DIF}\)\(=\dfrac{180^0}{2}= 90^o\)
Vậy các góc \(DIE\) và góc \(DIF\) là những góc vuông.
c) \(I\) là trung điểm của \( EF\) nên \(IE = IF =\dfrac{{EF}}{2} = \dfrac{{10}}{2}= 5\,cm.\)
Áp dụng định lí Pytago vào \(∆DEI\) vuông tại \(I\) (do theo câu b góc \(DIE\) vuông) ta có:
\(\eqalign{
& D{E^2} = D{I^2} + E{I^2} \cr
& \Rightarrow D{I^2} = D{E^2}-E{I^2} \cr
& \,\,\,\,\,\,\,\,D{I^2}\, = {13^2}-{5^2} = 144 \cr
& \Rightarrow DI = 12\,\,cm \cr} \)













Danh sách bình luận