 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 4. Tính chất ba đường trung tuyến của tam giác
Bài 4. Tính chất ba đường trung tuyến của tam giác
Bài 27 trang 67 SGK Toán 7 tập 2
Hãy chứng minh định lí đảo của định lí
Đề bài
Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Chứng minh tam giác \(ABC\) cân tại \(A\) ta chứng minh \(\widehat B = \widehat C\) hoặc \(AB = AC.\)
Lời giải chi tiết
Ta đưa về bài toán: Cho \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G.\) Biết \(BM=CN\), chứng minh tam giác \(ABC\) là tam giác cân.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\).
Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
+) \(BC\) là cạnh chung
+) \(CN = BM\) (giả thiết)
+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân) (điều phải chứng minh).
Loigiaihay.com




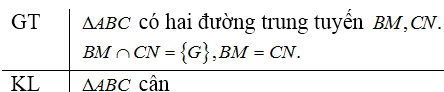








Danh sách bình luận