Bài 1 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo

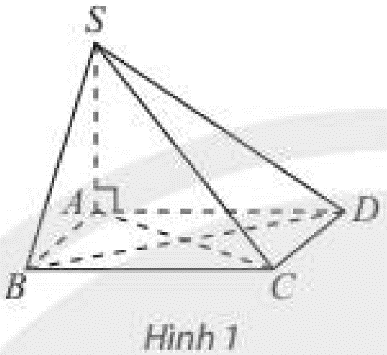
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình vuông, (SA) vuông góc với mặt đáy.

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(SA\) vuông góc với mặt đáy. Đường thẳng \(C{\rm{D}}\) vuông góc với mặt phẳng nào sau đây?

A. \(\left( {SAD} \right)\).

B. \(\left( {SAC} \right)\).

C. \(\left( {SAB} \right)\).

D. \(\left( {SBD} \right)\).

Phương pháp giải - Xem chi tiết

Sử dụng định lí 1: Nếu đường thẳng \(d\) vuông góc với hai đường thẳng cắt nhau \(a\) và \(b\) cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).

Lời giải chi tiết

Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\).

\(ABCD\) là hình vuông \( \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)

\( \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\)

Chọn A.

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Bài 2 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(b\), \(SA\) vuông góc với mặt đáy, \(SC = 2b\sqrt 2 \).
Bài 3 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp (S.ABCD) có các cạnh bên và cạnh đáy đều bằng (a).
Bài 4 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp tam giác đều (S.ABC) cạnh đáy bằng (2a) và chiều cao bằng (asqrt 2 ).
Bài 5 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ bằng \(a\) và chiều cao bằng \(\frac{{a\sqrt 6 }}{3}\) là
Bài 6 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho chóp tứ giác \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 4a,\) \(AD = 3a\). Các cạnh bên đều có độ dài \(5a\). Góc nhị diện \(\left[ {S,BC,A} \right]\) có số đo là
Bài 7 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Nếu hình hộp chữ nhật có ba kích thước là \(3;4;5\) thì độ dài đường chéo của nó là:
Bài 8 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng \(a\) là
Bài 9 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình vuông \(ABCD\) và tam giác đều \(SAB\) cạnh \(a\) nằm trong hai mặt phẳng vuông góc với nhau. Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\).
Bài 10 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\).
Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\)
Bài 12 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo
Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\)
Bài 13 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình hộp \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = a\), đáy \(ABCD\) là hình thoi có \(AB = BD = a\).