 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Giải bài tập 4 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho tứ giác ABCD có (widehat B = widehat D = {90^o}). a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn. b) So sánh độ dài của AC và BD.
Đề bài
Cho tứ giác ABCD có \(\widehat B = \widehat D = {90^o}\).
a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh độ dài của AC và BD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) - Sử dụng tính chất đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
- Chứng mình A, B, C, D cách đều 1 điểm nên nằm trên 1 đường tròn.
b) Dựa vào quan hệ giữa đường kính và dây cung.
Lời giải chi tiết
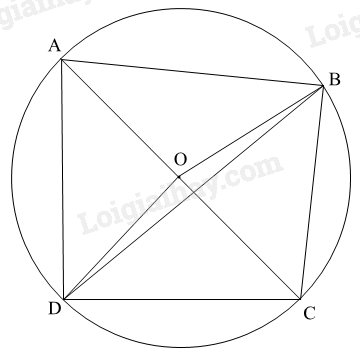
a) Gọi O là trung điểm của AC.
Xét tam giác ABC vuông tại B có O là trung điểm của AC nên \(OA = OB = OC = \frac{1}{2} AC\)
Xét tam giác ADC vuông tại D có O là trung điểm của AC nên \(OA = OD = OC = \frac{1}{2} AC\)
Suy ra \(OA = OB = OC = OD = \frac{1}{2} AC\) nên A, B, C, D cùng nằm trên một đường tròn tâm O đường kính AC.
b) Xét đường tròn tâm O đường kính AC có BD là dây cung không đi qua tâm O nên AC > BD.
- Giải bài tập 5 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 7 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận