 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Đề bài
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu đề bài để vẽ hình
- Áp dụng khoảng cách từ tâm đến đường tròn để chứng minh 4 điểm thuộc đường tròn
- Bán kính đường tròn bằng nửa đường chéo hình chữ nhật.
Lời giải chi tiết
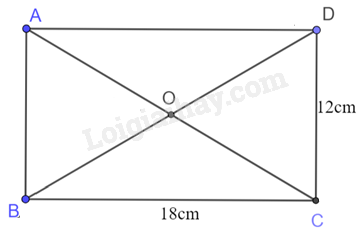
Ta có ABCD là hình chữ nhật và gọi O là giao của hai đường chéo AC và BD.
Nên ta có OA = OB = OC = OD suy ra bốn điểm A, B, C, D cùng thuộc đường tròn tâm O, bán kính OA.
Áp dụng định lí Pythagore vào tam giác vuông ACD, ta có:
\(AC = \sqrt {AD^2 + CD^2} = \sqrt {18^2 + 12^2} = 6\sqrt {13}\)
Suy ra R = OA = \(\frac{{AC}}{2} = \frac{{6\sqrt {13}}}{2} = 3\sqrt {13}cm\).
- Giải bài tập 3 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 4 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 5 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 7 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận