-
Toán 9 tập 1 - Chân trời sáng tạo
-
Toán 9 tập 2 - Chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Bài 2. Hình nón - Toán 9 Chân trời sáng tạo
Lý thuyết Hình nón Toán 9 Chân trời sáng tạo
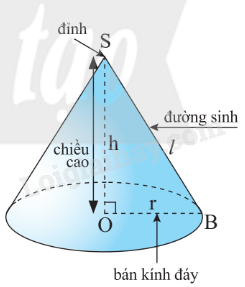
1. Hình nón Định nghĩa Khi quay tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón. – S gọi là đỉnh của hình nón. – Cạnh OB quét thành hình tròn gọi là đáy của hình nón. Bán kính của đáy gọi là bán kính đáy của hình nón. – Cạnh SB quét thành mặt xung quanh của hình nón. Mỗi vị trí của SB là một đường sinh. – Độ dài SO là chiều cao của hình nón.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
1. Hình nón
Định nghĩa
|
Khi quay tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón.
– S gọi là đỉnh của hình nón. – Cạnh OB quét thành hình tròn gọi là đáy của hình nón. Bán kính của đáy gọi là bán kính đáy của hình nón. – Cạnh SB quét thành mặt xung quanh của hình nón. Mỗi vị trí của SB là một đường sinh. – Độ dài SO là chiều cao của hình nón. |
Chú ý: Độ dài đường sinh l của hình nón có bán kính đáy r và chiều cao h được tính bởi công thức:
\(l = \sqrt {{r^2} + {h^2}} \).
Ví dụ:
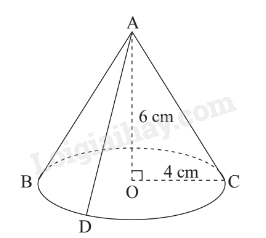
Hình nón có:
+ A là đỉnh;
+ chiều cao là 6cm;
+ bán kính đáy là 4cm.
+ các đường sinh là: AB, AC, AD.
2. Diện tích xung quanh của hình nón
Diện tích xung quanh của hình nón
|
Diện tích xung quanh \({S_{xq}}\) của hình nón có bán kính đáy r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\). |
Diện tích toàn phần của hình nón
|
Diện tích toàn phần \({S_{tp}}\) của hình nón có bán kính đáy r, độ dài đường sinh l là: \({S_{tp}} = {S_{xq}} + S = \pi rl + \pi {r^2}\) (S là diện tích đáy của hình nón). |
Ví dụ:
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \left( {c{m^2}} \right)\).
3. Thể tích của hình nón
|
Thể tích V của hình nón có bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón). |
Ví dụ:
Tam giác SOB vuông tại O nên theo định lí Pythagore ta có:
\(\begin{array}{l}O{B^2} + S{O^2} = S{B^2}\\{6^2} + S{O^2} = {10^2}\\S{O^2} = 100 - 36 = 64\\SO = 8cm.\end{array}\)
Thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \left( {c{m^3}} \right)\).
Bình luận
Chia sẻ
- Giải mục 1 trang 88, 89 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải mục 3 trang 91 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 1 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
