Giải Bài 76 trang 90 sách bài tập toán 7 - Cánh diều

Cho tam giác nhọn ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên cạnh AC lấy điểm E sao cho \(A{\rm{E}} = \frac{1}{3}AC\).

Đề bài

Cho tam giác nhọn ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên cạnh AC lấy điểm E sao cho \(A{\rm{E}} = \frac{1}{3}AC\).

a) Chứng minh E là trọng tâm tam giác BCD.

b) Gọi M là trung điểm DC. Chứng minh ba điểm B, M, E thẳng hàng.

Lời giải chi tiết

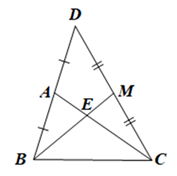
a) Ta có \(A{\rm{E}} = \frac{1}{3}AC\)nên \(CE = \frac{2}{3}AC\)

Trong tam giác BCD có CA là trung tuyến và \(CE = \frac{2}{3}AC\).

Suy ra E là trọng tâm tam giác BCD.

Vậy E là trọng tâm tam giác BCD.

b) Trong tam giác BCD có CA và BM là hai đường trung tuyến nên BM cắt CA tại trọng tâm của tam giác.

Mà E là trọng tâm của tam giác BCD (theo câu a) nên điểm E thuộc đường thẳng BM.

Hay ba điểm B, E, M thẳng hàng.

Vậy ba điểm B, E, M thẳng hàng.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Giải Bài 77 trang 90 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC cân tại A có đường trung tuyến AD, G là trọng tâm. Trên tia đối của tia DA lấy điểm E sao cho DE = DG.
Giải Bài 78 trang 90 sách bài tập toán 7 - Cánh diều
Cho tam giác DEF cân tại D có đường trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho MN = ME.
Giải Bài 75 trang 90 sách bài tập toán 7 - Cánh diều
Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng (widehat {BAC} = 90^circ )
Giải Bài 74 trang 90 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M, N lần lượt là trung điểm của BC, CE. Gọi I, K lần lượt là giao điểm của AM, AN với BE. Chứng minh BI = IK = KE.
Giải Bài 73 trang 90 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC đều và có G là trọng tâm.
Giải Bài 72 trang 90 sách bài tập toán 7 - Cánh diều
Chứng minh: Nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Giải Bài 71 trang 89 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG lấy điểm D sao cho MD = MG.
Giải Bài 70 trang 89 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G. Chứng minh: a) BM = CN;