Đề thi học kì 2 Toán 11 Cánh diều - Đề số 5
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Cho các số thực \(a,b,\alpha \left( {a > 0;b > 0} \right)\). Mệnh đề nào sau đây đúng?
-
A.
\({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }\)
-
B.
\({\left( {a - b} \right)^\alpha } = {a^\alpha } - {b^\alpha }\)
-
C.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^{ - \alpha }}}}\)
-
D.
\({\left( {a + b} \right)^\alpha } = {a^\alpha } + {b^\alpha }\)
Cho \[{\log _a}b = 3\] và \[{\log _a}c = 2\]. Tính \[P = {\log _a}\left( {b{c^2}} \right)\]
-
A.
7.
-
B.
4.
-
C.
-1.
-
D.
0.
Cho hàm số \[f\left( x \right) = \ln \left( {{x^2} - 2x + 4} \right)\]. Tìm các giá trị của \(x\) để \[f'\left( x \right) > 0\]?
-
A.
\(x \ne 1\)
-
B.
\(x > 0\)
-
C.
\(x > 1\)
-
D.
\(\forall x\)
Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
-
A.
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
-
B.
\(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\)
-
C.
\(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\)
-
D.
\(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\)
Gieo một con xúc xắc có sáu mặt, các mặt 1, 2, 3, 4 được sơn đỏ, mặt 5, 6 sơn xanh. Gọi A là biến cố được mặt số lẻ, B là biến cố được mặt sơn màu đỏ. Xác suất của \(A \cap B\) là:
-
A.
\(\frac{1}{3}.\)
-
B.
\(\frac{1}{4}.\)
-
C.
\(\frac{2}{3}.\)
-
D.
\(\frac{3}{4}.\)
Cho hàm số \(y = f(x)\) có đồ thị \((C)\) và đạo hàm \(f'(2) = 6.\) Hệ số góc của tiếp tuyến của \((C)\) tại điểm \(M\left( {2;f\left( 2 \right)} \right)\) bằng
-
A.
2
-
B.
3
-
C.
6
-
D.
12
Cho hàm số \(f\left( x \right) = {\left( {x + 1} \right)^3}.\) Giá trị của \(f''\left( 1 \right)\) bằng?
-
A.
12
-
B.
6
-
C.
24
- D.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật và \(SA \bot (ABCD).\) Mệnh đề nào dưới đây đúng ?
-
A.
\(BC \bot (SAD).\)
-
B.
\(AB \bot (SAD).\)
-
C.
\(AC \bot (SAD).\)
-
D.
\(BD \bot (SAD).\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\)\(SA \bot (ABCD)\) và \(SA = a.\) Góc giữa đường thẳng \(SB\) và mặt phẳng \((ABCD)\) bằng:
-
A.
\(45^\circ .\)
-
B.
\(90^\circ .\)
-
C.
\(30^\circ .\)
-
D.
\(60^\circ .\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot (ABCD),\)\(AB = a\) và \(SB = \sqrt 2 a.\) Khoảng cách từ điểm \(S\) đến mặt phẳng \((ABCD)\) bằng?
-
A.
\(a.\)
-
B.
\(\sqrt 2 a.\)
-
C.
\(2a.\)
-
D.
\(\sqrt 3 a.\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H,K lần lượt là hình chiếu của A lên SC, SD. Kí hiệu \(d(A,(SCD))\) là khoảng cách giữa điểm A và mặt phẳng\((SCD)\). Khẳng định nào sau đây đúng:
- A.
- B.
- C.
-
D.
\(d(A,(SCD)) = AD\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H,K lần lượt là hình chiếu của A lên SC, SD. Khẳng định nào sau đây đúng:
-
A.
\(BD \bot (SAC)\)
-
B.
\(AK \bot (SCD)\)
-
C.
\(BC \bot (SAC)\)
-
D.
\(AH \bot (SCD)\)
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = {t^2} - 2t\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \(2{t_0} - 2\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(8\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 10\)là \(16(m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 3s\)là 5 (m/s)
Cho hàm số có đồ thị (C): \(y = f\left( x \right) = {x^2} + x + 1\,\,(C)\)
a) Không tồn tại phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là\(y = x + 1\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = 3\) là \(y = - 3x - 3\)
Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\). Có đáy là hình vuông và cạnh bên bằng \(2a\). Hình chiếu của \(A'\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm của cạnh \(AD\), đường thẳng \(A'C\) hợp với mặt phẳng \(\left( {ABCD} \right)\)một góc \({45^o}\).
a) \(A'H \bot AC\)
b) A’H không vuông góc (BB’C’C)
c) \(\left( {A'C,(ABCD)} \right) = \widehat {A'CH}\)
d) Thể tích khối lăng trụ bằng \(4{a^3}\sqrt 5 \)
Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,7.
a) Xác suất để cả hai động cơ đều chạy tốt là 0,56
b) Xác suất để cả hai hai động cơ đều chạy không tốt là 0,06
c) Xác suất để có ít nhất một động cơ chạy tốt là 0,06
d) Xác suất để chỉ có 1 động cơ chạy tốt 0,3
Lời giải và đáp án
Cho các số thực \(a,b,\alpha \left( {a > 0;b > 0} \right)\). Mệnh đề nào sau đây đúng?
-
A.
\({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }\)
-
B.
\({\left( {a - b} \right)^\alpha } = {a^\alpha } - {b^\alpha }\)
-
C.
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^{ - \alpha }}}}\)
-
D.
\({\left( {a + b} \right)^\alpha } = {a^\alpha } + {b^\alpha }\)
Đáp án : A
Sử dụng công thức tính lũy thừa
\({\left( {ab} \right)^\alpha } = {a^\alpha }.{b^\alpha }\)
\({\left( {\frac{a}{b}} \right)^\alpha } = \frac{{{a^\alpha }}}{{{b^\alpha }}}\)
Đáp án A.
Cho \[{\log _a}b = 3\] và \[{\log _a}c = 2\]. Tính \[P = {\log _a}\left( {b{c^2}} \right)\]
-
A.
7.
-
B.
4.
-
C.
-1.
-
D.
0.
Đáp án : A
Sử dụng công thức logarit
\[P = {\log _a}\left( {b{c^2}} \right) = {\log _a}b + {\log _a}{c^2} = {\log _a}b + 2{\log _a}c = 3 + 2.2 = 7\]
Đáp án A.
Cho hàm số \[f\left( x \right) = \ln \left( {{x^2} - 2x + 4} \right)\]. Tìm các giá trị của \(x\) để \[f'\left( x \right) > 0\]?
-
A.
\(x \ne 1\)
-
B.
\(x > 0\)
-
C.
\(x > 1\)
-
D.
\(\forall x\)
Đáp án : C
Sử dụng công thức tính đạo hàm của hàm hợp
\[\begin{array}{l}f'\left( x \right) = \left[ {\ln \left( {{x^2} - 2x + 4} \right)} \right]' = \frac{{\left( {{x^2} - 2x + 4} \right)'}}{{{x^2} - 2x + 4}} = \frac{{2x - 2}}{{{x^2} - 2x + 4}}\\f'\left( x \right) > 0 \Leftrightarrow \frac{{2x - 2}}{{{x^2} - 2x + 4}} > 0 \Leftrightarrow 2x - 2 > 0 \Leftrightarrow x > 1\end{array}\]
Đáp án C.
Cho \(A\), \(B\) là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
-
A.
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
-
B.
\(P\left( {A \cup B} \right) = P\left( A \right).P\left( B \right)\)
-
C.
\(P\left( {A \cup B} \right) = P\left( A \right) - P\left( B \right)\)
-
D.
\(P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\)
Gieo một con xúc xắc có sáu mặt, các mặt 1, 2, 3, 4 được sơn đỏ, mặt 5, 6 sơn xanh. Gọi A là biến cố được mặt số lẻ, B là biến cố được mặt sơn màu đỏ. Xác suất của \(A \cap B\) là:
-
A.
\(\frac{1}{3}.\)
-
B.
\(\frac{1}{4}.\)
-
C.
\(\frac{2}{3}.\)
-
D.
\(\frac{3}{4}.\)
Đáp án : B
Sử dụng quy tắc xác suất
Biến cố \(A \cap B\)là :”Gieo được mặt xuất hiện số lẻ và sơn đỏ” \( \Rightarrow n\left( {A \cap B} \right) = 2\)
Vậy xác suất cần tính là \(P(A \cap B) = \frac{2}{6} = \frac{1}{3}\)
Đáp án B.
Cho hàm số \(y = f(x)\) có đồ thị \((C)\) và đạo hàm \(f'(2) = 6.\) Hệ số góc của tiếp tuyến của \((C)\) tại điểm \(M\left( {2;f\left( 2 \right)} \right)\) bằng
-
A.
2
-
B.
3
-
C.
6
-
D.
12
Đáp án : C
Đạo hàm của hàm số\(y = f(x)\) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm \({M_0}({x_0};f({x_0}))\)
Khi đó phương trình tiếp tuyến của (C) tại điểm M0 là: \(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Hệ số góc của tiếp tuyến của \((C)\) tại điểm \(M\left( {2;f\left( 2 \right)} \right)\)là \(f'(2) = 6.\)
Đáp án C.
Cho hàm số \(f\left( x \right) = {\left( {x + 1} \right)^3}.\) Giá trị của \(f''\left( 1 \right)\) bằng?
-
A.
12
-
B.
6
-
C.
24
- D.
Đáp án : A
Sử dụng công thức tính đạo hàm của hàm hợp
\[\begin{array}{l}f'\left( x \right) = \left[ {{{\left( {x + 1} \right)}^3}} \right]' = 3(x + 1)'{\left( {x + 1} \right)^2} = 3{\left( {x + 1} \right)^2}\\f''\left( x \right) = \left[ {3{{\left( {x + 1} \right)}^2}} \right]' = 6(x + 1)'\left( {x + 1} \right) = 6\left( {x + 1} \right)\\f''(1) = 12\end{array}\]
Đáp án A.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật và \(SA \bot (ABCD).\) Mệnh đề nào dưới đây đúng ?
-
A.
\(BC \bot (SAD).\)
-
B.
\(AB \bot (SAD).\)
-
C.
\(AC \bot (SAD).\)
-
D.
\(BD \bot (SAD).\)
Đáp án : B
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
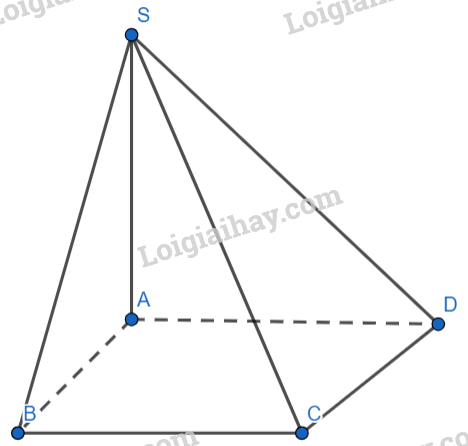
a) \(\left\{ \begin{array}{l}BC//AD\\BC \not\subset (SAD),AD \subset (SAD)\end{array} \right. \Rightarrow BC//(SAD)\)
b) \[\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow AB \bot (SAD)\]
Đáp án B.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\)\(SA \bot (ABCD)\) và \(SA = a.\) Góc giữa đường thẳng \(SB\) và mặt phẳng \((ABCD)\) bằng:
-
A.
\(45^\circ .\)
-
B.
\(90^\circ .\)
-
C.
\(30^\circ .\)
-
D.
\(60^\circ .\)
Đáp án : A
Sử dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
Do \(SA \bot (ABCD)\)
Nên AB là hình chiếu của SA lên mp(ABCD)
Ta có: \(\left( {SB,(ABCD)} \right) = \left( {SB,AB} \right)\)
Xét tam giác SAB vuông tại A ta có:
\(\begin{array}{l}\left( {SB,AB} \right) = \widehat {SBA}\\\tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {SBA} = {45^0}\end{array}\)
Đáp án A.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot (ABCD),\)\(AB = a\) và \(SB = \sqrt 2 a.\) Khoảng cách từ điểm \(S\) đến mặt phẳng \((ABCD)\) bằng?
-
A.
\(a.\)
-
B.
\(\sqrt 2 a.\)
-
C.
\(2a.\)
-
D.
\(\sqrt 3 a.\)
Đáp án : A
Sử dụng công thức tính khoảng cách từ điểm đến mặt phẳng
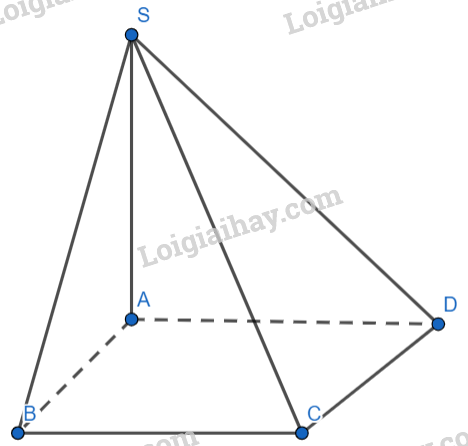
\(Do\,\,SA \bot (ABCD) \Rightarrow d(S,(ABCD)) = SA\)
Tam giác SAB vuông tại A nên \(SA = \sqrt {S{B^2} - A{B^2}} = a\)
Đáp án A.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H,K lần lượt là hình chiếu của A lên SC, SD. Kí hiệu \(d(A,(SCD))\) là khoảng cách giữa điểm A và mặt phẳng\((SCD)\). Khẳng định nào sau đây đúng:
- A.
- B.
- C.
-
D.
\(d(A,(SCD)) = AD\)
Đáp án : A
Sử dụng công thức tính khoảng cách từ điểm đến mặt phẳng
Ta có:
\[\begin{array}{l}\left\{ \begin{array}{l}DC \bot AD\\DC \bot SA\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow DC \bot (SAD) \Rightarrow DC \bot AK\\\left\{ \begin{array}{l}AK \bot SD\\AK \bot DC\\SD,DC \subset (SDC)\\SD \cap DC\end{array} \right. \Rightarrow AK \bot (SDC) \Rightarrow d(A,(SCD)) = AK\end{array}\]
Đáp án A.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H,K lần lượt là hình chiếu của A lên SC, SD. Khẳng định nào sau đây đúng:
-
A.
\(BD \bot (SAC)\)
-
B.
\(AK \bot (SCD)\)
-
C.
\(BC \bot (SAC)\)
-
D.
\(AH \bot (SCD)\)
Đáp án : B
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
\[\begin{array}{l}\left\{ \begin{array}{l}DC \bot AD\\DC \bot SA\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow DC \bot (SAD) \Rightarrow DC \bot AK\\\left\{ \begin{array}{l}AK \bot SD\\AK \bot DC\\SD,DC \subset (SDC)\\SD \cap DC\end{array} \right. \Rightarrow AK \bot (SDC)\end{array}\]
Đáp án B.
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = {t^2} - 2t\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \(2{t_0} - 2\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(8\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 10\)là \(16(m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 3s\)là 5 (m/s)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \(2{t_0} - 2\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(8\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 10\)là \(16(m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 3s\)là 5 (m/s)
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
Phương trình gia tốc của chất điểm: \(a(t) = v'(t)\)
a) Đạo hàm của hàm số \(s(t)\)tại thời điểm \({t_0}\)
Ta có:
\(\begin{array}{l}f'({t_0}) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f(t) - f({t_0})}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{{t^2} - 2t - ({t_0}^2 - 2{t_0})}}{{t - {t_0}}}} \right)\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{(t - {t_0})(t + {t_0} - 2)}}{{t - {t_0}}}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \left( {t + {t_0} - 2} \right) = 2{t_0} - 2\end{array}\)
b) Phương trình vận tốc của chất điểm là: \(v(t) = s' = s'(t) = 2t - 2\)
Vận tốc tức thời của chuyển động tại thời điểm t = 5 (s) là: \(v(5) = 2.5 - 2 = 8(m.s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 10\)là \(v(10) = 2.10 - 2 = 18\,(m/s)\)
d) Trong khoảng thời gian từ \(t = 0\) tới \(t = 3s\)thì chất điểm di chuyển được quãng đường: \({3^2} - 2.3 = 3(m)\)
Suy ra vận tốc trung bình của chất điểm trong khoảng thời gian 3s kể từ thời điểm \(t = 0\) là:
\(\overline v = \frac{{\Delta s}}{{\Delta t}} = \frac{{3 - 0}}{{3 - 0}} = 1(m/s)\)
Cho hàm số có đồ thị (C): \(y = f\left( x \right) = {x^2} + x + 1\,\,(C)\)
a) Không tồn tại phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là\(y = x + 1\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = 3\) là \(y = - 3x - 3\)
a) Không tồn tại phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là\(y = x + 1\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = 3\) là \(y = - 3x - 3\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3: Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
a) Vì \((C)\) không cắt Ox nên không tồn tại tiếp tuyển thỏa mãn yêu cầu bài toán
b) Tọa độ giao điểm của \((C)\) với trục Oy là: \((0;1)\)
Suy ra phương trình tiếp tuyến tại giao điểm \((C)\) với trục Ox là:
\(y = y'(0)(x - 0) + 1 \Leftrightarrow y = x + 1\)
c) Tọa độ giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là nghiệm của phương trình :
\({x^2} + x + 1 = x + 1 \Leftrightarrow {x^2} = 0 \Leftrightarrow x = 0\)
Phương trình tiếp tuyến tại điểm \((0;1)\)là \(y = x + 1\)
d) Gọi \(M(a;b)\) là tiếp điểm của tiếp tuyến của đồ thị \((C)\) với hệ số góc \(k = - 3\)
\( \Rightarrow y'(a)) = - 3 \Leftrightarrow 2a + 1 = - 3 \Leftrightarrow a = - 2\)
Suy ra phương trình tiếp tuyến với hệ số góc \(k = - 3\) là \(y = - 3(x + 2) + 3 \Leftrightarrow y = - 3x - 3\)
Cho lăng trụ tứ giác \(ABCD.A'B'C'D'\). Có đáy là hình vuông và cạnh bên bằng \(2a\). Hình chiếu của \(A'\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm của cạnh \(AD\), đường thẳng \(A'C\) hợp với mặt phẳng \(\left( {ABCD} \right)\)một góc \({45^o}\).
a) \(A'H \bot AC\)
b) A’H không vuông góc (BB’C’C)
c) \(\left( {A'C,(ABCD)} \right) = \widehat {A'CH}\)
d) Thể tích khối lăng trụ bằng \(4{a^3}\sqrt 5 \)
a) \(A'H \bot AC\)
b) A’H không vuông góc (BB’C’C)
c) \(\left( {A'C,(ABCD)} \right) = \widehat {A'CH}\)
d) Thể tích khối lăng trụ bằng \(4{a^3}\sqrt 5 \)
Sử dụng định lý đường thẳng vuông góc với mặt phẳng; góc giữa đường thẳng với mặt phẳng
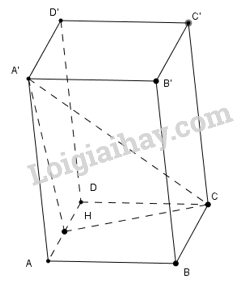
a) \(A'H \bot (ABCD) \Rightarrow A'H \bot AC\)
b) A’H không vuông góc (BB’C’C)
c)d) Ta có: \(A'H \bot (ABCD)\)
\( \Rightarrow HC\)là hình chiếu của \(A'C\) trên \(\left( {ABCD} \right)\)
\( \Rightarrow (\widehat {A'C,(ABCD)}) = (\widehat {A'C,HC}) = \widehat {HCA'} = {45^o}\)
Áp dụng định lý Pitago cho tam giác HDC vuông tại D ta có:
\(HC = \sqrt {H{D^2} + D{C^2}} = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = a\sqrt 5 \)
\( \Rightarrow A'H = HC.\tan {45^o} = a\sqrt 5 \)
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = a\sqrt 5 .{\left( {2a} \right)^2} = 4{a^3}\sqrt 5 \).
Một chiếc máy có hai động cơ I và II hoạt động độc lập với nhau.Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,8 và 0,7.
a) Xác suất để cả hai động cơ đều chạy tốt là 0,56
b) Xác suất để cả hai hai động cơ đều chạy không tốt là 0,06
c) Xác suất để có ít nhất một động cơ chạy tốt là 0,06
d) Xác suất để chỉ có 1 động cơ chạy tốt 0,3
a) Xác suất để cả hai động cơ đều chạy tốt là 0,56
b) Xác suất để cả hai hai động cơ đều chạy không tốt là 0,06
c) Xác suất để có ít nhất một động cơ chạy tốt là 0,06
d) Xác suất để chỉ có 1 động cơ chạy tốt 0,3
Sử dụng công thức nhân xác suất cho hai biến cố độc lập
Gọi A là biến cố động cơ I chạy tốt
B là biến cố động cơ II chạy tốt
Theo giả thiết: \(P(A) = 0,8;P(B) = 0,7\)
\( \Rightarrow P(\overline A ) = 1 - 0,8 = 0,2;P(\overline B ) = 1 - 0,7 = 0,3\)
a)Gọi X là biến cố cả 2 động cơ cùng chạy tốt
Ta có X=A.B
Mà 2 biến cố A và B độc lập với nhau nên:
\(P(X) = P(A).P(B) = 0,8.0,7 = 0,56\)
b)Gọi Y là biến cố cả 2 động cơ cùng không chạy tốt
Ta có: \(Y = \overline A .\overline B \)
Mà 2 biến cố \(\overline A \); \(\overline B \) độc lập với nhau nên: \(P(Y) = P(\overline A ).P(\overline B ) = 0,2.0,3 = 0,06\)
c) Ta có biến cố: \(\overline Y \) là ít nhất 1 động cơ chạy tốt
\(P(\overline Y ) = 1 - P(Y) = 1 - 0,06 = 0,94\)
d)Gọi Z là biến cố chỉ có một động cơ chạy tốt
\(P(Z) = P(A).P(\overline B ) + P(\overline A ).P(B) = 0,8.0,3 + 0,2.0,7 = 0,38\)
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
Phương trình gia tốc của chất điểm: \(a(t) = v'(t)\)
Ta có: \(a\left( t \right) = v'\left( t \right) = s''\left( t \right)\)
\(s\left( t \right) = {t^3} - 3{t^2} - 9t \Rightarrow s'\left( t \right) = 3{t^2} - 6t - 9 \Rightarrow s''\left( t \right) = 6t - 6\)
Vậy gia tốc tức thời tại thời điểm \(t = 3s\) là \(a\left( 3 \right) = 6.3 - 6 = 12m/{s^2}.\)
Sử dụng công thức tính đạo hàm của hàm hợp
\(y = \frac{{{x^2} - x + 3}}{{x + 1}} \Rightarrow y' = \frac{{{x^2} + 2x - 4}}{{{{\left( {x + 1} \right)}^2}}}\)
Do đó: \(a + b + c = 1 + 2 - 4 = - 1.\)
Sử dụng công thức tính trung vị
Tổng số vận động viên n = 5 + 12 + 32 + 45 + 30 = 124
Gọi x1; x2; ...; x124 lần lượt là thời gian chạy của 124 vận động viên tham gia hội thao được xếp theo thứ tự không giảm.
Ta có: x1; ...; x5 ∈ [21; 21,5), x6; ...; x17 ∈ [21,5; 22), x18; ...; x49 ∈ [22; 22,5), x50; ...; x94 ∈ [22,5; 23), x95; ...; x124 ∈ [23; 23,5).
Số trung vị của dãy số liệu là: \[\frac{{\left( {{x_{62}} + {x_{63}}} \right)}}{2}\]
Mà x62; x63 ∈ [22,5; 23) do đó: \({M_e} = 22,5 + \frac{{\frac{{124}}{2} - 49}}{{45}}\left( {23 - 22,5} \right) \approx 22,6\)
Vậy ban tổ chức nên chọn vận động viên có thời gian chạy không quá 22,6 giây.
Sử dụng phương pháp xác định khoảng cách giữa hai đường thẳng
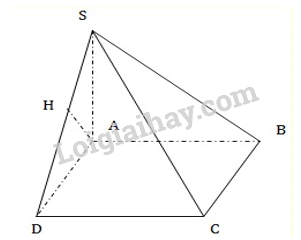
Từ \(A\) kẻ \(AH \bot SD \Rightarrow AH\)là đường vuông góc chung
Chứng minh: Ta có \(AB \bot AH\,\,\left( {Do\,\,AB \bot \left( {SAD} \right)} \right)\)và \(AH \bot SD \Rightarrow AH\)là đường vuông góc chung
\( \Rightarrow d\left( {AB,\,\,SD} \right) = AH.\)
Tính \(AH:\) \(AH = \frac{{AS.AD}}{{\sqrt {A{S^2} + A{D^2}} }} = \frac{{2a.2a}}{{\sqrt {{{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} }} = a\sqrt 2 .\)
Sử dụng phương pháp tính đạo hàm theo định nghĩa
Theo định nghĩa đạo hàm của hàm số tại một điểm:
\(f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 1} \right)\left( {x - 2} \right)....\left( {x - 1000} \right)}}{x}\)
\( = \mathop {\lim }\limits_{x \to 0} \left[ {\left( {x - 1} \right)\left( {x - 2} \right)....\left( {x - 1000} \right)} \right] = \left( { - 1} \right).\left( { - 2} \right).\left( { - 3} \right)....\left( { - 1000} \right) = 1000!\)
Vậy \(f'\left( 0 \right) = 1000!\)
Lập phương trình diện tích tam giác và tính diện tích theo a
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\},\,\,\)\(y' = - \frac{{2{a^2}}}{{{x^2}}}.\)
Tiếp tuyến của đồ thị hàm số \(y = \frac{{2{a^2}}}{x}\) tại điểm \(\left( {{x_0};\frac{{2{a^2}}}{{{x_0}}}} \right)\)là đường thẳng \(\left( d \right)\) có dạng:
\(y = - \frac{{2{a^2}}}{{{x_0}^2}}.\left( {x - {x_0}} \right) + \frac{{2{a^2}}}{{{x_0}}},\,\,\left( {{x_0} \ne 0,a \ne 0} \right).\)
+ Gọi \(A = d \cap Ox:\)Cho\(y = 0 \Rightarrow - \frac{{2{a^2}}}{{{x_0}^2}}\left( {x - {x_0}} \right) + \frac{{2{a^2}}}{{{x_0}}} = 0 \Leftrightarrow x - {x_0} - {x_0} = 0 \Leftrightarrow x = 2{x_0} \Rightarrow A\left( {2{x_0};0} \right).\)
+ Gọi \(B = d \cap Oy:\) Cho \(x = 0 \Rightarrow y = - \frac{{2{a^2}}}{{{x_0}^2}}.\left( { - {x_0}} \right) + \frac{{2{a^2}}}{{{x_0}}} = \frac{{2{a^2}}}{{{x_0}}} + \frac{{2{a^2}}}{{{x_0}}} = \frac{{4{a^2}}}{{{x_0}}} \Rightarrow B\left( {0;\frac{{4{a^2}}}{{{x_0}}}} \right).\)
+ Diện tích tam giác \(OAB\): \(S = \frac{1}{2}OA.OB = \frac{1}{2}.\left| {2{x_0}} \right|.\left| {\frac{{4{a^2}}}{{{x_0}}}} \right| = 4{a^2}\)
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Với b,c là hai số thực dương tùy ý thỏa mãn ({rm{lo}}{{rm{g}}_5}b ge {rm{lo}}{{rm{g}}_5}c), khẳng định nào dưới đây là đúng? A. (b ge c). B. (b le c). C. (b > c). D. (b < c).
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP 1. Một số yếu tố thống kê và xác suất - Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm - Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất 2. Hàm số mũ và hàm số logarit - Phép tính lũy thừa với số mũ thực - Phép tính logarit - Hàm số mũ và hàm số logarit - Phương trình, bất phương trình mũ và logarit
>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
