Đề thi giữa kì 2 Toán 11 Cánh diều - Đề số 8
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.
Đề bài
Với \(a \ne 0\), \(b \ne 0\) và m, n là các số nguyên thì
-
A.
\({a^m}.{a^n} = {a^{m - n}}\)
-
B.
\({a^m}.{a^n} = {a^{m.n}}\)
-
C.
\({a^m}.{a^n} = {a^{m + n}}\)
-
D.
\({a^m}.{a^n} = {a^{\frac{m}{n}}}\)
Cho số thực a \((0 < a \ne 1)\) và M, N là các số thực dương. Chọn khẳng định đúng trong các khẳng định sau:
-
A.
\({\log _a}(MN) = {\log _a}M - {\log _a}N\)
-
B.
\({\log _a}(MN) = {\log _a}M.{\log _a}N\)
-
C.
\({\log _a}(MN) = {\log _a}M - {\log _a}N\)
-
D.
\({\log _a}(MN) = {\log _a}M + {\log _a}N\)
Trong các hàm số sau, hàm số nào sau đây là hàm số mũ?
-
A.
\(y = {x^2}\)
-
B.
\(y = {2^x}\)
-
C.
\(y = {x^\pi }\)
-
D.
\(y = \sqrt x \)
Bất phương trình \({\log _{0,3}}(x - 1) \le {\log _{0,3}}(2x + 1)\) có tập xác định là
-
A.
\(D = \left[ {1; + \infty } \right)\)
-
B.
\(D = \left( { - \frac{1}{2}; + \infty } \right)\)
-
C.
\(D = \left( {1; + \infty } \right)\)
-
D.
\(D = \left[ { - \frac{1}{2}; + \infty } \right)\)
Cho hai biến cố A và B là hai biến cố xung khắc. Biết \(P(A) = \frac{1}{4}\), \(P(A \cup B) = \frac{1}{2}\). Tính P(B).
-
A.
\(\frac{1}{8}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{3}\)
-
D.
\(\frac{3}{4}\)
Một chiếc máy có hai chiếc động cơ I và II chạy độc lập nhau. Xác suất để động cơ I và II chạy tốt lần lượt là 0,8 và 0,7. Xác suất để cả hai động cơ chạy tốt là
-
A.
0,24
-
B.
0,94
-
C.
0,14
-
D.
0,56
Khảo sát khối lượng 30 củ khoai tây ngẫu nhiên thu hoạch được ở một nông trường:
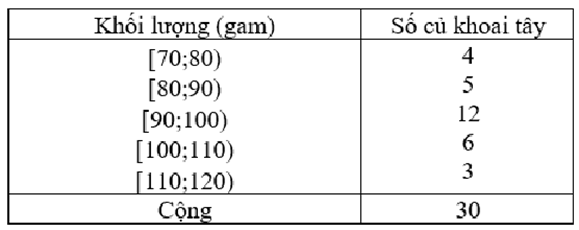
Số củ khoai tây đạt chuẩn loại I (từ 90 gam đến dưới 100 gam) là
-
A.
5
-
B.
12
-
C.
6
-
D.
4
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và \(SA \bot (ABC)\). Khẳng định nào sau đây là đúng?
-
A.
\(AB \bot (SAC)\)
-
B.
\(AB \bot (SAC)\)
-
C.
\(BC \bot (SAB)\)
-
D.
\(BC \bot (SAC)\)
Nếu một khối chóp có diện tích đáy là S và có chiều cao là h thì thể tích V của nó được tính theo công thức nào sau đây?
-
A.
\(V = Sh\)
-
B.
\(V = \frac{1}{3}Sh\)
-
C.
\(V = \frac{1}{6}Sh\)
-
D.
\(V = \frac{2}{3}Sh\)
-
A.
\((SAC) \bot (SBD)\)
-
B.
\((SAC) \bot (SCD)\)
-
C.
\((SAC) \bot (SAD)\)
-
D.
\((SAC) \bot (SAB)\)
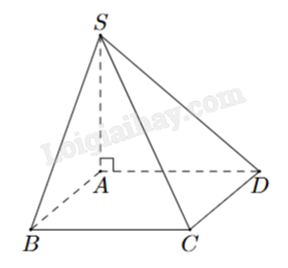
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. SA = 2a vuông góc với mặt đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SAD) là
-
A.
\(a\)
-
B.
\(2a\)
-
C.
\(a\sqrt 3 \)
-
D.
\(\frac{a}{3}\)
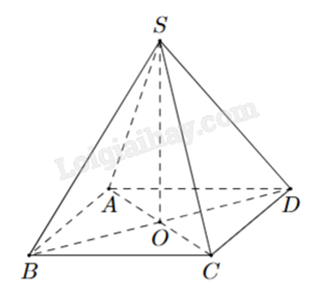
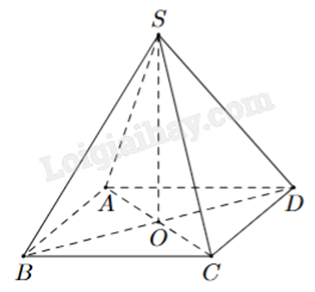
Cho hình chóp S.ABCD như hình bên. Có đáy ABCD là hình chữ nhật. SA = SC và SB = SD. Khẳng định nào sau đây là đúng?
-
A.
\(SO \bot (SAB)\)
-
B.
\(OC \bot (SBD)\)
-
C.
\(SO \bot (ABCD)\)
-
D.
\(AB \bot (SAB)\)
Số lượng người đi xem một bộ phim mới theo độ tuổi trong một rạp chiếu phim (sau 1 giờ đầu công chiếu) được ghi lại theo bảng phân phối ghép nhóm sau:

a) Giá trị đại diện nhóm [50;60) là 55.
b) Độ tuổi được dự báo là ít xem phim đó nhất thuộc nhóm [50;60).
c) Nhóm chứa mốt là [30;40).
d) Độ tuổi được dự báo là thích xem phim đó nhiều nhất là 32 tuổi.
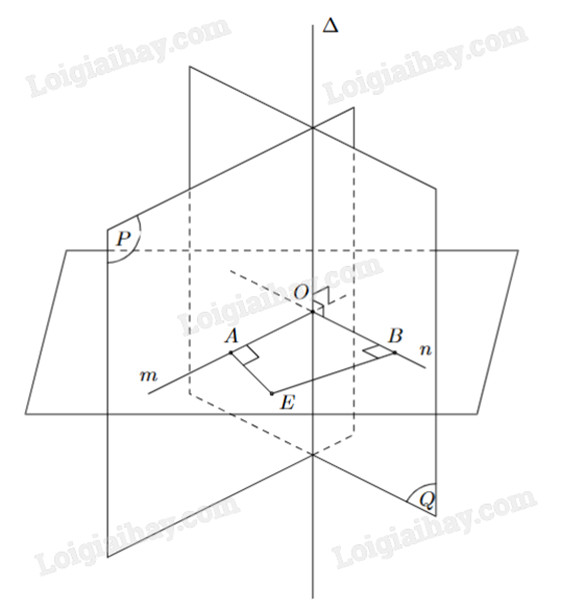
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến \(\Delta \) như hình vẽ. Lấy một điểm O bất kì thuộc đường thẳng \(\Delta \). Gọi m, n là các đường thẳng đi qua O, tương ứng thuôc (P), (Q) và vuông góc với \(\Delta \).
a) Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng \(\Delta \) và m.
b) Góc giữa hai mặt phẳng (P) và (Q) là góc \(\widehat {AOB}\) (nếu \(\widehat {AOB} < {90^o}\)) hoặc \({180^o} - \widehat {AOB}\) (nếu \({90^o} < \widehat {AOB} < {180^o}\)).
c) Nếu \(\widehat {AOB} = {90^o}\) thì ta nói \((P) \bot (Q)\).
d) Giả sử góc
\(\widehat {AOB} = {120^o}\) thì ta nói góc giữa hai mặt phẳng (P) và (Q) là \({120^o}\).
Trong một nghiên cứu, một nhóm học sinh được cho xem cùng một danh sách các loài động vật và được kiểm tra lại xem họ còn nhớ bao nhiêu phần trăm danh sách đó sau mỗi tháng. Giả sử sau t tháng, khả năng nhớ trung bình của nhóm học sinh đó được tính theo công thức \(M(t) = 75 - 20\ln (t + 1)\), \(0 \le t \le 12\) (đơn vị: %). Hãy tính khả năng nhớ trung bình của nhóm học sinh đó sau 8 tháng (kết quả làm tròn đến hàng phần chục).
Đáp án:
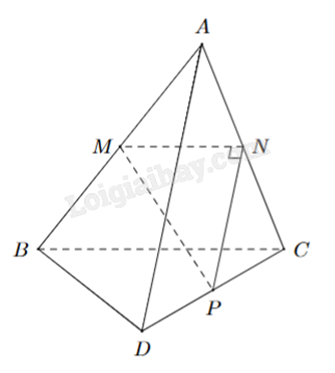
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP)). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (hình vẽ). Tính góc giữa hai đường thẳng AD và BC.
Đáp án:
Trong một lớp 10 có 50 học sinh. Khi đăng ký cho học phụ đạo thi có 38 học sinh đăng ký học Toán, 30 học sinh đăng ký học Lý, 25 học sinh đăng ký học cả Toán và Lý. Nếu chọn ngẫu nhiên 1 học sinh của lớp đó thì xác suất để em này không đăng ký học phụ đạo môn nào cả là bao nhiêu (viết kết quả dưới dạng số thập phân)?
Đáp án:
Thời gian (phút) truy cập internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tìm trung vị của mẫu số liệu ghép nhóm trên (kết quả viết dưới dạng số thập phân).
Đáp án:
Lời giải và đáp án
Với \(a \ne 0\), \(b \ne 0\) và m, n là các số nguyên thì
-
A.
\({a^m}.{a^n} = {a^{m - n}}\)
-
B.
\({a^m}.{a^n} = {a^{m.n}}\)
-
C.
\({a^m}.{a^n} = {a^{m + n}}\)
-
D.
\({a^m}.{a^n} = {a^{\frac{m}{n}}}\)
Đáp án : C
Áp dụng tính chất lũy thừa.
\({a^m}.{a^n} = {a^{m + n}}\).
Cho số thực a \((0 < a \ne 1)\) và M, N là các số thực dương. Chọn khẳng định đúng trong các khẳng định sau:
-
A.
\({\log _a}(MN) = {\log _a}M - {\log _a}N\)
-
B.
\({\log _a}(MN) = {\log _a}M.{\log _a}N\)
-
C.
\({\log _a}(MN) = {\log _a}M - {\log _a}N\)
-
D.
\({\log _a}(MN) = {\log _a}M + {\log _a}N\)
Đáp án : D
Áp dụng tính chất logarit.
\({\log _a}(MN) = {\log _a}M + {\log _a}N\).
Trong các hàm số sau, hàm số nào sau đây là hàm số mũ?
-
A.
\(y = {x^2}\)
-
B.
\(y = {2^x}\)
-
C.
\(y = {x^\pi }\)
-
D.
\(y = \sqrt x \)
Đáp án : B
Hàm số mũ có dạng \(y = {a^x}\).
\(y = {2^x}\) là hàm số mũ.
Bất phương trình \({\log _{0,3}}(x - 1) \le {\log _{0,3}}(2x + 1)\) có tập xác định là
-
A.
\(D = \left[ {1; + \infty } \right)\)
-
B.
\(D = \left( { - \frac{1}{2}; + \infty } \right)\)
-
C.
\(D = \left( {1; + \infty } \right)\)
-
D.
\(D = \left[ { - \frac{1}{2}; + \infty } \right)\)
Đáp án : C
\(y = {\log _a}x\) có tập xác định là \(D = \left( {0; + \infty } \right)\).
ĐKXĐ: \(\left\{ \begin{array}{l}x - 1 > 0\\2x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x > - \frac{1}{2}\end{array} \right. \Leftrightarrow x > 1\). Vậy \(D = \left( {1; + \infty } \right)\).
Cho hai biến cố A và B là hai biến cố xung khắc. Biết \(P(A) = \frac{1}{4}\), \(P(A \cup B) = \frac{1}{2}\). Tính P(B).
-
A.
\(\frac{1}{8}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{3}\)
-
D.
\(\frac{3}{4}\)
Đáp án : B
Với hai biến cố A, B xung khắc, ta có \(P(A \cup B) = P(A) + P(B)\).
\(P(A \cup B) = P(A) + P(B) \Leftrightarrow P(B) = P(A \cup B) - P(A) = \frac{1}{2} - \frac{1}{4} = \frac{1}{4}\).
Một chiếc máy có hai chiếc động cơ I và II chạy độc lập nhau. Xác suất để động cơ I và II chạy tốt lần lượt là 0,8 và 0,7. Xác suất để cả hai động cơ chạy tốt là
-
A.
0,24
-
B.
0,94
-
C.
0,14
-
D.
0,56
Đáp án : D
Áp dụng công thức nhân xác suất.
Hai chiếc động cơ hoạt động độc lập với nhau nên xác suất để cả hai động cơ chạy tốt là 0,8.0,7 = 0,56.
Khảo sát khối lượng 30 củ khoai tây ngẫu nhiên thu hoạch được ở một nông trường:

Số củ khoai tây đạt chuẩn loại I (từ 90 gam đến dưới 100 gam) là
-
A.
5
-
B.
12
-
C.
6
-
D.
4
Đáp án : B
Số củ khoai tây đạt chuẩn loại I (từ 90 gam đến dưới 100 gam) là tần số của nhóm [90;100).
Số củ khoai tây đạt chuẩn loại I (từ 90 gam đến dưới 100 gam) là 12.
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và \(SA \bot (ABC)\). Khẳng định nào sau đây là đúng?
-
A.
\(AB \bot (SAC)\)
-
B.
\(AB \bot (SAC)\)
-
C.
\(BC \bot (SAB)\)
-
D.
\(BC \bot (SAC)\)
Đáp án : A
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
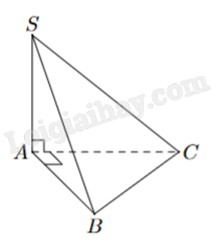
Ta có \(\left\{ \begin{array}{l}SA \bot (ABC) \Rightarrow SA \bot AB\\AC \bot AB\end{array} \right. \Rightarrow AB \bot (SAC)\).
Nếu một khối chóp có diện tích đáy là S và có chiều cao là h thì thể tích V của nó được tính theo công thức nào sau đây?
-
A.
\(V = Sh\)
-
B.
\(V = \frac{1}{3}Sh\)
-
C.
\(V = \frac{1}{6}Sh\)
-
D.
\(V = \frac{2}{3}Sh\)
Đáp án : B
Áp dụng công thức tính thể tích của khối chóp.
Thể tích khối chóp có diện tích đáy là S và có chiều cao là h là \(V = \frac{1}{3}Sh\).
-
A.
\((SAC) \bot (SBD)\)
-
B.
\((SAC) \bot (SCD)\)
-
C.
\((SAC) \bot (SAD)\)
-
D.
\((SAC) \bot (SAB)\)
Đáp án : A
Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.
S.ABCD là chóp tứ giác đều nên ABCD là hình vuông. Do đó \(AC \bot BD\).
Mặt khác, \(SO \bot AC\). Ta có \(\left\{ \begin{array}{l}SO \bot AC\\BD \bot AC\end{array} \right. \Rightarrow AC \bot (SBD) \Rightarrow (SAC) \bot (SBD)\).
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a. SA = 2a vuông góc với mặt đáy (ABCD). Khoảng cách từ điểm B đến mặt phẳng (SAD) là

-
A.
\(a\)
-
B.
\(2a\)
-
C.
\(a\sqrt 3 \)
-
D.
\(\frac{a}{3}\)
Đáp án : A
Tìm hình chiếu vuông góc của B lên (SAD) rồi tính khoảng cách từ B đến hình chiếu đó.
Ta có \(\left\{ \begin{array}{l}SA \bot (ABCD) \Rightarrow SA \bot AB\\AD \bot AB\end{array} \right. \Rightarrow AB \bot (SAD)\).
Do đó, A là hình chiếu vuông góc của B lên (SAD).
Khoảng cách từ B đến (SAD) là AB = a.
Cho hình chóp S.ABCD như hình bên. Có đáy ABCD là hình chữ nhật. SA = SC và SB = SD. Khẳng định nào sau đây là đúng?

-
A.
\(SO \bot (SAB)\)
-
B.
\(OC \bot (SBD)\)
-
C.
\(SO \bot (ABCD)\)
-
D.
\(AB \bot (SAB)\)
Đáp án : C
Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
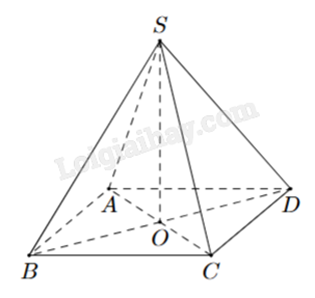
O là tâm hình chữ nhật ABCD nên O là trung điểm của AC và BD.
Theo giả thiết, các tam giác SAC và SBD cân tại S nên SO vừa là đường trung tuyến, vừa là đường cao của hai tam giác.
Suy ra \(\left\{ \begin{array}{l}SO \bot AC\\SO \bot BD\end{array} \right. \Rightarrow SO \bot (ABCD)\).
Số lượng người đi xem một bộ phim mới theo độ tuổi trong một rạp chiếu phim (sau 1 giờ đầu công chiếu) được ghi lại theo bảng phân phối ghép nhóm sau:

a) Giá trị đại diện nhóm [50;60) là 55.
b) Độ tuổi được dự báo là ít xem phim đó nhất thuộc nhóm [50;60).
c) Nhóm chứa mốt là [30;40).
d) Độ tuổi được dự báo là thích xem phim đó nhiều nhất là 32 tuổi.
a) Giá trị đại diện nhóm [50;60) là 55.
b) Độ tuổi được dự báo là ít xem phim đó nhất thuộc nhóm [50;60).
c) Nhóm chứa mốt là [30;40).
d) Độ tuổi được dự báo là thích xem phim đó nhiều nhất là 32 tuổi.
a) Giá trị đại diện của nhóm là trung bình cộng hai đầu mút của nhóm.
b) Độ tuổi được dự báo là ít xem phim đó nhất thuộc nhóm có tần số nhỏ nhất.
c) Nhóm chứa mốt có tần số lớn nhất trong bảng số liệu.
d) Công thức tính mốt thuộc nhóm \([{u_m};{u_{m + 1}})\):
\({M_o} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right)+\left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\); trong đó \({n_m}\) là tần số nhóm thứ m.
a) Đúng. Giá trị đại diện của nhóm [50;60) là \(\frac{{50 + 60}}{2} = 55\).
b) Đúng. Độ tuổi được dự báo là ít xem phim đó nhất thuộc nhóm [50;60) vì có tần số nhỏ nhất là 2.
c) Đúng. Nhóm chứa mốt là [30;40) vì có tần số lớn nhất là 16.
d) Sai. Độ tuổi được dự báo là thích xem phim đó nhiều nhất là mốt của mẫu số liệu:
\({M_o} = 30 + \frac{{16 - 12}}{{\left( {16 - 12} \right)+\left( {16 - 7} \right)}}.\left( {40 - 30} \right) = \frac{{280}}{9} \approx 33\).
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến \(\Delta \) như hình vẽ. Lấy một điểm O bất kì thuộc đường thẳng \(\Delta \). Gọi m, n là các đường thẳng đi qua O, tương ứng thuôc (P), (Q) và vuông góc với \(\Delta \).

a) Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng \(\Delta \) và m.
b) Góc giữa hai mặt phẳng (P) và (Q) là góc \(\widehat {AOB}\) (nếu \(\widehat {AOB} < {90^o}\)) hoặc \({180^o} - \widehat {AOB}\) (nếu \({90^o} < \widehat {AOB} < {180^o}\)).
c) Nếu \(\widehat {AOB} = {90^o}\) thì ta nói \((P) \bot (Q)\).
d) Giả sử góc
\(\widehat {AOB} = {120^o}\) thì ta nói góc giữa hai mặt phẳng (P) và (Q) là \({120^o}\).
a) Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng \(\Delta \) và m.
b) Góc giữa hai mặt phẳng (P) và (Q) là góc \(\widehat {AOB}\) (nếu \(\widehat {AOB} < {90^o}\)) hoặc \({180^o} - \widehat {AOB}\) (nếu \({90^o} < \widehat {AOB} < {180^o}\)).
c) Nếu \(\widehat {AOB} = {90^o}\) thì ta nói \((P) \bot (Q)\).
d) Giả sử góc
\(\widehat {AOB} = {120^o}\) thì ta nói góc giữa hai mặt phẳng (P) và (Q) là \({120^o}\).
Áp dụng quy tắc xác định góc giữa hai mặt phẳng. Quy ước góc giữa hai mặt phẳng có số đo từ 0 đến 90 độ.
a) Sai. Ta có \(\left\{ \begin{array}{l}(P) \cap (Q) = \Delta \\m \bot \Delta ,m \subset (P)\\n \bot \Delta ,n \subset (Q)\end{array} \right. \Rightarrow \left( {(P),(Q)} \right) = \left( {m,n} \right)\).
b) Đúng. Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng m và n, hay góc \(\widehat {AOB}\) (nếu \(\widehat {AOB} < {90^o}\)) hoặc \({180^o} - \widehat {AOB}\) (nếu \({90^o} < \widehat {AOB} < {180^o}\)).
c) Đúng. Nếu \(\widehat {AOB} = {90^o}\) thì ta nói \((P) \bot (Q)\).
d) Sai. Giả sử góc \(\widehat {AOB} = {120^o}\) thì ta nói góc giữa hai mặt phẳng (P) và (Q) là \({180^o} - {120^o} = {60^o}\).
Trong một nghiên cứu, một nhóm học sinh được cho xem cùng một danh sách các loài động vật và được kiểm tra lại xem họ còn nhớ bao nhiêu phần trăm danh sách đó sau mỗi tháng. Giả sử sau t tháng, khả năng nhớ trung bình của nhóm học sinh đó được tính theo công thức \(M(t) = 75 - 20\ln (t + 1)\), \(0 \le t \le 12\) (đơn vị: %). Hãy tính khả năng nhớ trung bình của nhóm học sinh đó sau 8 tháng (kết quả làm tròn đến hàng phần chục).
Đáp án:
Đáp án:
Tính M(8) (thay t = 8 vào công thức đề bài cho và tính giá trị).
Khả năng nhớ trung bình của nhóm học sinh đó sau 8 tháng là \(M(8) = 75 - 20\ln (8 + 1) \approx 31,1\)%.
Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP)). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (hình vẽ). Tính góc giữa hai đường thẳng AD và BC.

Đáp án:
Đáp án:
Nếu a // c, b // d thì (a,b) = (c,d).
Áp dụng tính chất của đường trung bình trong tam giác, ta có NP // AD, MN // BC.
Vậy \((AD,BC) = (NP,MN) = \widehat {MNP} = {90^o}\).
Trong một lớp 10 có 50 học sinh. Khi đăng ký cho học phụ đạo thi có 38 học sinh đăng ký học Toán, 30 học sinh đăng ký học Lý, 25 học sinh đăng ký học cả Toán và Lý. Nếu chọn ngẫu nhiên 1 học sinh của lớp đó thì xác suất để em này không đăng ký học phụ đạo môn nào cả là bao nhiêu (viết kết quả dưới dạng số thập phân)?
Đáp án:
Đáp án:
Áp dụng công thức cộng xác suất.
A: “Chọn được học sinh đăng ký học Toán”.
B: “Chọn được học sinh đăng ký học Lý”.
\(A \cap B\): “Chọn được học sinh đăng ký cả Toán và Lý”.
\(A \cup B\): “Chọn được học sinh đăng ký học phụ đạo”.
Xác suất chọn được học sinh đăng ký học phụ đạo là: \(P(A \cup B) = P(A) + P(B) - P(A \cap B) = \frac{{38}}{{50}} + \frac{{30}}{{50}} - \frac{{25}}{{50}} = \frac{{43}}{{50}}\).
Xác suất để chọn ra học sinh không đăng ký môn nào là: \(1 - \frac{{43}}{{50}} = \frac{7}{{50}} = 0,14\).
Thời gian (phút) truy cập internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Tìm trung vị của mẫu số liệu ghép nhóm trên (kết quả viết dưới dạng số thập phân).
Đáp án:
Đáp án:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Cỡ mẫu: n = 3 + 12 + 15 + 24 + 2 = 56.
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian học sinh truy cập internet sắp xếp theo thứ tự không giảm.
Có \(\frac{n}{2} = \frac{{56}}{2} = 28\) nên \({Q_2} = \frac{{{x_{28}} + {x_{29}}}}{2} \in [15,5;18,5)\).
\({Q_2} = 15,5 + \frac{{\frac{{56}}{2} - (3 + 12)}}{{15}}.(18,5 - 15,5) = 18,1\).
Tính \(\frac{{M(24)}}{{M(0)}}\).
Khối lượng vi khuẩn ở thời điểm ban đầu là \(M(0) = 50.1,{06^0} = 50\) (g).
Khối lượng vi khuẩn sau 24 giờ là \(M(24) = 50.1,{06^{24}}\) (g).
Khối lượng vi khuẩn sau 24 giờ gấp \(\frac{{50.1,{{06}^{24}}}}{{50}} \approx 4\) lần khối lượng vi khuẩn ban đầu.
Áp dụng các công thức biến đổi logarit: \({\log _a}b = x \Leftrightarrow b = {a^x}\); \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
Gọi độ pH của dung dịch A là \(p{H_A}\), độ pH của dung dịch B là \(p{H_B}\); nồng độ ion \({H^ + }\) của dung dịch A là \({x_A}\), nồng độ ion \({H^ + }\) của dung dịch B là \({x_B}\).
Theo giả thiết:
\(p{H_A} - p{H_B} = 0,6 \Leftrightarrow - \left( {\log {x_A} - \log {x_B}} \right) = 0,6 \Leftrightarrow \log {x_B} - \log {x_A} = 0,6\)
\( \Leftrightarrow \log \frac{{{x_B}}}{{{x_A}}} = 0,6 \Leftrightarrow \frac{{{x_B}}}{{{x_A}}} = {10^{0,6}} \approx 4\).
Xác định đoạn thẳng thể hiện khoảng cách giữa AB và SC. Từ đó, áp dụng hệ thức lượng trong tam giác vuông để tìm chiều cao khối chóp và tính thể tích.
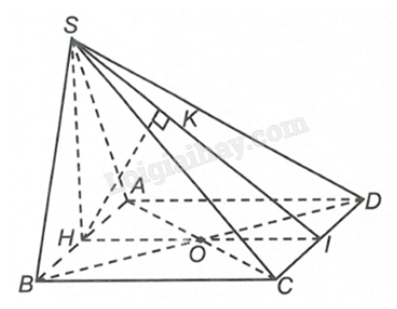
Gọi H, I lần lượt là trung điểm của AB, CD. Kẻ \(HK \bot SI\).
SH vừa là đường cao, vừa là đường trung tuyến của tam giác cân SAB, suy ra \(SH \bot AB\).
Mà \((SAB) \bot (ABCD)\), \((SAB) \cap (ABCD) = AB\) nên \(SH \bot (ABCD) \Rightarrow SH \bot CD\).
Ta có \(\left\{ \begin{array}{l}SH \bot CD\\HI \bot CD\end{array} \right. \Rightarrow CD \bot (SHI) \Rightarrow CD \bot HK\).
Mặt khác \(\left\{ \begin{array}{l}HK \bot SI\\HK \bot CD\end{array} \right. \Rightarrow HK \bot (SCD)\).
Vì CD // AB nên \(d\left( {AB,DC} \right) = d\left( {AB,(SCD)} \right) = d\left( {H,(SCD)} \right) = HK\).
Ta có \(HK = \frac{3}{2}\), \(HI = AD = \sqrt 3 \).
Xét tam giác vuông SHI vuông tại H có đường cao HK:
\(\frac{1}{{H{K^2}}} = \frac{1}{{H{S^2}}} + \frac{1}{{H{I^2}}} \Leftrightarrow \frac{1}{{H{S^2}}} = \frac{1}{{H{K^2}}} - \frac{1}{{H{I^2}}} = \frac{1}{{{{\left( {\frac{3}{2}} \right)}^2}}} - \frac{1}{{{{\left( {\sqrt 3 } \right)}^2}}} = \frac{1}{9} \Leftrightarrow HS = 3\).
Thể tích khối chóp là \({V_{S.ABCD}} = \frac{1}{3}.SH.{S_{ACBD}} = \frac{1}{3}.SH.AB.AD = \frac{1}{3}.3.1.\sqrt 3 = \sqrt 3 \approx 1,73\).
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.
Phần trắc nghiệm (3 điểm) Câu 1: Chọn đáp án đúng.
Phần trắc nghiệm (7 điểm) Câu 1: Chọn đáp án đúng. Với a là số thực khác 0 thì:
Phần trắc nghiệm (7 điểm) Câu 1: Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Cho $a>0,m,n\in \mathbb{R}$. Khẳng định nào sau đây là đúng?
Phần trắc nghiệm (7 điểm) Câu 1: Cho số thực dương a và số hữu tỉ $r=\frac{m}{n}$, trong đó $m,n\in \mathbb{Z},n>0$. Ta có:
Câu 1: Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận