Đề thi học kì 1 Toán 11 Cánh diều - Đề số 8
Tổng hợp đề thi giữa kì 2 lớp 11 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Phần trắc nghiệm
Đề bài
Khi biểu diễn trên đường tròn lượng giác, góc lượng giác nào trong các góc lượng giác có số đo dưới đây có cùng điểm cuối với góc lượng giác có số đo \(\frac{\pi }{4}\)?
-
A.
\(\frac{{10\pi }}{3}\)
-
B.
\( - \frac{{5\pi }}{4}\)
-
C.
\(\frac{{25\pi }}{4}\)
-
D.
\(\frac{{7\pi }}{4}\)
Cho \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây đúng?
-
A.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) > 0\)
-
B.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) \ge 0\)
-
C.
\(\tan \left( {\alpha + \pi } \right) < 0\)
-
D.
\(\tan \left( {\alpha + \pi } \right) > 0\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{( - 1)}^{n - 1}}}}{{n + 1}}\). Số hạng thứ 9 của dãy là
-
A.
\({u_9} = \frac{1}{{10}}\)
-
B.
\({u_9} = \frac{{ - 1}}{{10}}\)
-
C.
\({u_9} = \frac{{ - 1}}{9}\)
-
D.
\({u_9} = \frac{1}{9}\)
Trong các dãy số sau, dãy số nào là một cấp số cộng?
-
A.
1; -2; -4; -6; -8
-
B.
1; -3; -6; -9; -12
-
C.
1; -3; -7; -11; -15
-
D.
1; -3; -5; -7; -9
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 4\), công bội q = 3. Giá trị của \({u_2}\) bằng
-
A.
8
-
B.
9
-
C.
6
-
D.
12
Giới hạn \(\lim \frac{1}{{2n + 5}}\) bằng
-
A.
\(\frac{1}{2}\)
-
B.
0
-
C.
\( + \infty \)
-
D.
\(\frac{1}{5}\)
Cho hàm số \(f(x) = \frac{{2x - 1}}{{x + 2}}\). Hàm số gián đoạn tại điểm
-
A.
\({x_0} = - 2\)
-
B.
\({x_0} = \frac{1}{2}\)
-
C.
\({x_0} = 2\)
-
D.
\({x_0} = 1\)
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Mặt phẳng hoàn toàn xác định khi biết nó đi qua hai điểm
-
B.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng
-
C.
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa
-
D.
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó
Cho tứ diện ABCD. Cặp đường thẳng nào sau đây chéo nhau?
-
A.
AB, AD
-
B.
AB, CB
-
C.
BC, BD
-
D.
BC, AD
Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
-
A.
Hình chữ nhật
-
B.
Hình thang
-
C.
Hình bình hành
-
D.
Hình thoi
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\lim \left( {4 + {u_n}} \right) = 3\). Giá trị của \(\lim \left( {{u_n}} \right)\) bằng
-
A.
-1
-
B.
1
-
C.
7
-
D.
3
Công thức nào sau đây sai?
-
A.
\(\cos (a - b) = \cos a\cos b + \sin a\sin b\)
-
B.
\(\cos (a + b) = \cos a\cos b + \sin a\sin b\)
-
C.
\(\sin (a - b) = \sin a\cos b - \cos a\sin b\)
-
D.
\(\sin (a + b) = \sin a\cos b + \cos a\sin b\)
Cho hàm số y = sinx.
a) sinx < 0 khi \( - \frac{\pi }{2} < x < 0\).
b) Hàm số y = sinx là hàm số lẻ với mọi \(x \in \mathbb{R}\).
c) Phương trình sinx = 1 có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\).
d) Hàm số y = sinx có chặn dưới là 0.
Cho dãy số \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_1} = 2023;{u_2} = 2024\\2{u_{n + 1}} = {u_n} + {u_{n + 2}}\end{array} \right.\) với \(n \ge 1\).
a) Dãy \(\left( {{v_n}} \right):{v_n} = {u_n} - {u_{n - 1}}\) là dãy không đổi.
b) Biểu thị \({u_n}\) qua \({u_{n - 1}}\) ta được \({u_n} = {u_{n - 1}} + 1\).
c) \({u_3} = 2025\).
d) \({u_{2024}} = 4044\).
Cho g(x) = \(\left\{ \begin{array}{l}\frac{{{x^2} - x - 6}}{{x + 2}}\\2x + a\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne - 2\\x = - 2\end{array}\).
a) \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = - 4\).
b) g(x) liên tục tại x = -2 thì a = 1.
c) g(x) liên tục tại x = -2 thì bộ ba số a; 2; 5 tạo thành một cấp số cộng.
d) g(x) liên tục tại x = -2 thì bộ ba số 1; a; 1 tạo thành một cấp số nhân.
Cho tứ diện ABCD có điểm G là trọng tâm tam giác ABD và điểm M thuộc cạnh BC sao cho MB = 2MC.
a) MG cắt AC.
b) MG//AB.
c) MG//(ACD).
d) \((BGM) \cap (ACD) = MG\).
Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức \(h = 30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right)\). Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên (viết kết quả ở dạng số thập phân)?
Đáp án:
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là 100 nghìn đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn đồng so với giá của mét khoan ngay trước đó. Một người cần khoan một giếng sâu 20 m để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
Đáp án:
Tìm công bội của cấp số nhân thỏa \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 135\\{u_4} + {u_5} + {u_6} = 40\end{array} \right.\).
Đáp án:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt x - 1}}{{{x^2} - 1}}\\{m^2}x\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\) liên tục tại điểm \({x_0} = 1\)?
Đáp án:
Cho tứ diện ABCD có I, J lần lượt là trung điểm của các cạnh BC và BD. Gọi (P) là mặt phẳng qua I, J và cắt hai cạnh AC và AD lần lượt tại M và N. Để IJNM là hình thoi thì AC = kAM và AB = mCD. Khi đó giá trị của k + m bằng bao nhiêu?
Đáp án:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng \(\left( \alpha \right)\) qua BD và song song với SA, mặt phẳng \(\left( \alpha \right)\) cắt SC tại K. Biết SK = mKC. Tính giá trị biểu thức \({m^2} + 2\).
Đáp án:
Lời giải và đáp án
Khi biểu diễn trên đường tròn lượng giác, góc lượng giác nào trong các góc lượng giác có số đo dưới đây có cùng điểm cuối với góc lượng giác có số đo \(\frac{\pi }{4}\)?
-
A.
\(\frac{{10\pi }}{3}\)
-
B.
\( - \frac{{5\pi }}{4}\)
-
C.
\(\frac{{25\pi }}{4}\)
-
D.
\(\frac{{7\pi }}{4}\)
Đáp án : C
Các góc lượng giác hơn kém nhau \(k2\pi \) có cùng điểm cuối.
Ta có \(\frac{{25\pi }}{4} = \frac{\pi }{4} + 3.2\pi \).
Cho \(0 < \alpha < \frac{\pi }{2}\). Khẳng định nào sau đây đúng?
-
A.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) > 0\)
-
B.
\(\cot \left( {\alpha + \frac{\pi }{2}} \right) \ge 0\)
-
C.
\(\tan \left( {\alpha + \pi } \right) < 0\)
-
D.
\(\tan \left( {\alpha + \pi } \right) > 0\)
Đáp án : D
Dựa vào vị trí điểm cuối của góc lượng giác để xét dấu.
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\frac{\pi }{2} < \alpha + \frac{\pi }{2} < \pi \). Khi đó \(\sin \left( {\alpha + \frac{\pi }{2}} \right) > 0\), \(\cos \left( {\alpha + \frac{\pi }{2}} \right) < 0\) suy ra \(\cot \left( {\alpha + \frac{\pi }{2}} \right) < 0\).
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\pi < \alpha + \pi < \frac{{3\pi }}{2}\). Khi đó \(\sin \left( {\alpha + \pi } \right) < 0\), \(\cos \left( {\alpha + \pi } \right) < 0\) suy ra \(\tan \left( {\alpha + \pi } \right) > 0\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{( - 1)}^{n - 1}}}}{{n + 1}}\). Số hạng thứ 9 của dãy là
-
A.
\({u_9} = \frac{1}{{10}}\)
-
B.
\({u_9} = \frac{{ - 1}}{{10}}\)
-
C.
\({u_9} = \frac{{ - 1}}{9}\)
-
D.
\({u_9} = \frac{1}{9}\)
Đáp án : A
Thay 9 vào n và tính.
\({u_9} = \frac{{{{( - 1)}^{9 - 1}}}}{{9 + 1}} = \frac{1}{{10}}\).
Trong các dãy số sau, dãy số nào là một cấp số cộng?
-
A.
1; -2; -4; -6; -8
-
B.
1; -3; -6; -9; -12
-
C.
1; -3; -7; -11; -15
-
D.
1; -3; -5; -7; -9
Đáp án : C
Dãy số \(\left( {{u_n}} \right)\) có tính chất \({u_{n + 1}} = {u_n} + d\) thì được gọi là một cấp số cộng.
Ta thấy dãy số 1; -3; -7; -11; -15 là một cấp số cộng có số hạng đầu và công sai d = -4.
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 4\), công bội q = 3. Giá trị của \({u_2}\) bằng
-
A.
8
-
B.
9
-
C.
6
-
D.
12
Đáp án : D
\({u_n} = {u_1}{q^{n - 1}}\).
\({u_2} = {u_1}q = 4.3 = 12\).
Giới hạn \(\lim \frac{1}{{2n + 5}}\) bằng
-
A.
\(\frac{1}{2}\)
-
B.
0
-
C.
\( + \infty \)
-
D.
\(\frac{1}{5}\)
Đáp án : B
Sử dụng quy tắc tính giới hạn của dãy số.
Ta có \(\lim (2n + 5) = + \infty \) suy ra \(\lim \frac{1}{{2n + 5}} = 0\).
Cho hàm số \(f(x) = \frac{{2x - 1}}{{x + 2}}\). Hàm số gián đoạn tại điểm
-
A.
\({x_0} = - 2\)
-
B.
\({x_0} = \frac{1}{2}\)
-
C.
\({x_0} = 2\)
-
D.
\({x_0} = 1\)
Đáp án : A
f(x) gián đoạn tại điểm mà hàm số không xác định.
Hàm số có tập xác định là \(D = \mathbb{R}\backslash \{ - 2\} \), do đó hàm số không liên tục tại \({x_0} = - 2\).
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Mặt phẳng hoàn toàn xác định khi biết nó đi qua hai điểm
-
B.
Tồn tại bốn điểm không cùng thuộc một mặt phẳng
-
C.
Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa
-
D.
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường
thẳng đều thuộc mặt phẳng đó
Đáp án : A
Sử dụng khái niệm, tính chất của đường thẳng, mặt phẳng trong không gian.
A sai vì mặt phẳng hoàn toàn xác định khi biết nó đi qua ba điểm.
Cho tứ diện ABCD. Cặp đường thẳng nào sau đây chéo nhau?
-
A.
AB, AD
-
B.
AB, CB
-
C.
BC, BD
-
D.
BC, AD
Đáp án : D
Dựa vào định nghĩa tứ diện.
BC, AD là hai đường chéo nhau.
Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau?
-
A.
Hình chữ nhật
-
B.
Hình thang
-
C.
Hình bình hành
-
D.
Hình thoi
Đáp án : B
Dựa vào tính chất của phép chiếu song song.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Vì hình chữ nhật có hai cặp cạnh song song nên hình chiếu của nó cũng phải là tứ giác có hai cặp cạnh song song hoặc trở thành một đoạn thẳng.
Vì hình thang chỉ có một cặp cạnh song song nên không thể là hình chiếu của hình chữ nhật.
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \(\lim \left( {4 + {u_n}} \right) = 3\). Giá trị của \(\lim \left( {{u_n}} \right)\) bằng
-
A.
-1
-
B.
1
-
C.
7
-
D.
3
Đáp án : A
Sử dụng tính chất của giới hạn.
\(\lim \left( {4 + {u_n}} \right) = 3 \Leftrightarrow \lim 4 + \lim {u_n} = 3 \Leftrightarrow \lim {u_n} = 3 - \lim 4 = 3 - 4 = - 1\).
Công thức nào sau đây sai?
-
A.
\(\cos (a - b) = \cos a\cos b + \sin a\sin b\)
-
B.
\(\cos (a + b) = \cos a\cos b + \sin a\sin b\)
-
C.
\(\sin (a - b) = \sin a\cos b - \cos a\sin b\)
-
D.
\(\sin (a + b) = \sin a\cos b + \cos a\sin b\)
Đáp án : B
Dựa vào công thức cộng lượng giác.
B sai vì \(\cos (a + b) = \cos a\cos b - \sin a\sin b\).
Cho hàm số y = sinx.
a) sinx < 0 khi \( - \frac{\pi }{2} < x < 0\).
b) Hàm số y = sinx là hàm số lẻ với mọi \(x \in \mathbb{R}\).
c) Phương trình sinx = 1 có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\).
d) Hàm số y = sinx có chặn dưới là 0.
a) sinx < 0 khi \( - \frac{\pi }{2} < x < 0\).
b) Hàm số y = sinx là hàm số lẻ với mọi \(x \in \mathbb{R}\).
c) Phương trình sinx = 1 có nghiệm \(x = \frac{\pi }{2} + k\pi \), \(k \in \mathbb{Z}\).
d) Hàm số y = sinx có chặn dưới là 0.
a) Dựa vào vị trí điểm cuối của góc lượng giác để nhận xét dấu của giá trị lượng giác.
b) Hàm số f(x) là hàm số lẻ khi thỏa mãn các điều kiện:
- Nếu \(x \in D\) thì \( - x \in D\).
- Có \(f( - x) = - f(x)\).
c) Sử dụng công thức nghiệm của phương trình lượng giác cơ bản.
d) Dựa vào tập giá trị của hàm số.
a) Đúng. \( - \frac{\pi }{2} < x < 0\) nên điểm cuối của góc lượng giác nằm ở góc phần tư thứ IV.
Khi đó sinx < 0.
b) Đúng. Tập xác định của hàm số y = sinx là \(D = \mathbb{R}\) nên \(x \in D\) thì \( - x \in D\).
Mặt khác \(f( - x) = \sin ( - x) = - \sin x = - f(x)\).
Vậy hàm số y = sinx là hàm số lẻ.
c) Sai. \(\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \), \(k \in \mathbb{Z}\).
d) Sai. Ta có \( - 1 \le \sin x \le 1\) nên hàm số y = sinx có chặn dưới là -1.
Cho dãy số \(\left( {{u_n}} \right)\) biết \(\left\{ \begin{array}{l}{u_1} = 2023;{u_2} = 2024\\2{u_{n + 1}} = {u_n} + {u_{n + 2}}\end{array} \right.\) với \(n \ge 1\).
a) Dãy \(\left( {{v_n}} \right):{v_n} = {u_n} - {u_{n - 1}}\) là dãy không đổi.
b) Biểu thị \({u_n}\) qua \({u_{n - 1}}\) ta được \({u_n} = {u_{n - 1}} + 1\).
c) \({u_3} = 2025\).
d) \({u_{2024}} = 4044\).
a) Dãy \(\left( {{v_n}} \right):{v_n} = {u_n} - {u_{n - 1}}\) là dãy không đổi.
b) Biểu thị \({u_n}\) qua \({u_{n - 1}}\) ta được \({u_n} = {u_{n - 1}} + 1\).
c) \({u_3} = 2025\).
d) \({u_{2024}} = 4044\).
Chứng minh dãy trên là cấp số cộng thông qua tính chất của cấp số cộng rồi sử dụng công thức số hạng tổng quát.
a) Đúng. Ta có \(2{u_{n + 1}} = {u_n} + {u_{n + 2}} \Leftrightarrow {u_n} = 2{u_{n + 1}} - {u_{n + 2}}\).
Từ đó, thay n - 1 vào n ta được \({u_{n - 1}} = 2{u_{n - 1 + 1}} - {u_{n - 1 + 2}} \Leftrightarrow {u_{n - 1}} = 2{u_n} - {u_{n + 1}} \Leftrightarrow 2{u_n} = {u_{n - 1}} + {u_{n + 1}} \Leftrightarrow {u_n} = \frac{{{u_{n - 1}} + {u_{n + 1}}}}{2}\).
Suy ra \(\left( {{u_n}} \right)\) là cấp số cộng, tức \({u_n} = {u_{n - 1}} + d\).
Do đó \({v_n} = {u_n} - {u_{n - 1}} = d\) không đổi.
b) Đúng. \(\left( {{u_n}} \right)\) là cấp số cộng với công sai \(d = {u_2} - {u_1} = 2024 - 2023 = 1\).
Do đó \({u_n} = {u_{n - 1}} + d = {u_{n - 1}} + 1\).
c) Đúng. \({u_3} = {u_2} + d = 2024 + 1 = 2025\).
d) Sai. \({u_{2024}} = {u_1} + (2024 - 1).d = 2023 + (2024 - 1).1 = 4046\).
Cho g(x) = \(\left\{ \begin{array}{l}\frac{{{x^2} - x - 6}}{{x + 2}}\\2x + a\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne - 2\\x = - 2\end{array}\).
a) \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = - 4\).
b) g(x) liên tục tại x = -2 thì a = 1.
c) g(x) liên tục tại x = -2 thì bộ ba số a; 2; 5 tạo thành một cấp số cộng.
d) g(x) liên tục tại x = -2 thì bộ ba số 1; a; 1 tạo thành một cấp số nhân.
a) \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = - 4\).
b) g(x) liên tục tại x = -2 thì a = 1.
c) g(x) liên tục tại x = -2 thì bộ ba số a; 2; 5 tạo thành một cấp số cộng.
d) g(x) liên tục tại x = -2 thì bộ ba số 1; a; 1 tạo thành một cấp số nhân.
Sử dụng quy tắc tính giới hạn của hàm số tại một điểm.
Hàm số f(x) liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
a) Sai \(\mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} \frac{{(x - 3)(x + 2)}}{{x + 2}} = \mathop {\lim }\limits_{x \to - 2} (x - 3) = - 2 - 3 = - 5\).
b) Sai. Ta có:
\(\mathop {\lim }\limits_{x \to - 2} g(x) = \mathop {\lim }\limits_{x \to - 2} \frac{{{x^2} - x - 6}}{{x + 2}} = - 5\);
\(g( - 2) = 2.( - 2) + a = a - 4\).
Để g(x) liên tục tại x = -2 thì \(\mathop {\lim }\limits_{x \to - 2} g(x) = g( - 2) \Leftrightarrow - 5 = a - 4 \Leftrightarrow a = - 1\).
c) Đúng. Bộ ba số -1; 2; 5 tạo thành cấp số cộng với công sai d = 3.
d) Đúng. Bộ ba số 1; -1; 1 tạo thành một cấp số nhân với công bội q = -1.
Cho tứ diện ABCD có điểm G là trọng tâm tam giác ABD và điểm M thuộc cạnh BC sao cho MB = 2MC.
a) MG cắt AC.
b) MG//AB.
c) MG//(ACD).
d) \((BGM) \cap (ACD) = MG\).
a) MG cắt AC.
b) MG//AB.
c) MG//(ACD).
d) \((BGM) \cap (ACD) = MG\).
Sử dụng các điều kiện, tính chất của đường thẳng và mặt phẳng song song.
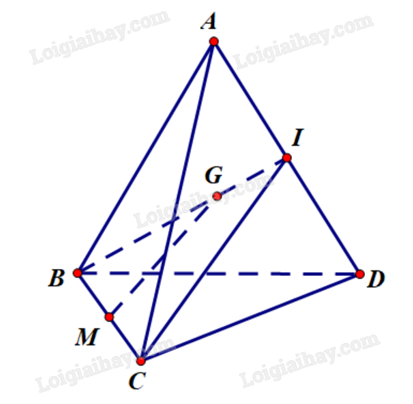
Gọi I là trung điểm của AD. Khi đó BI là đường trung tuyến tam giác ABD.
Suy ra \(\frac{{BG}}{{BI}} = \frac{2}{3}\).
Vì MB = 2MC suy ra \(\frac{{BM}}{{BC}} = \frac{2}{3}\).
Xét tam giác BCI có \(\frac{{BG}}{{BI}} = \frac{{BM}}{{BC}} = \frac{2}{3}\) suy ra MG//CI (định lí Thales đảo).
Mà \(MG\not{ \subset }(ACD)\), \(CI \subset (ACD)\) nên MG//(ACD).
a) Sai. Có MG//(ACD) mà \(AC \subset (ACD)\) nên MG không cắt AC.
b) Sai. MG và AB là hai đường thẳng chéo nhau.
c) Đúng. MG//(ACD).
d) Sai. Ta có:
Vì \(\left\{ \begin{array}{l}C \in BM \subset (BMG)\\C \in (ACD)\end{array} \right.\) nên \(C \in (BGM) \cap (ACD)\).
Vì \(\left\{ \begin{array}{l}I \in BG \subset (BMG)\\I \in AD \subset (ACD)\end{array} \right.\) nên \(I \in (BGM) \cap (ACD)\).
Vậy \((BGM) \cap (ACD) = CI\).
Chiều cao h (m) của một cabin trên vòng quay vào thời điểm t giây sau khi bắt đầu chuyển động được cho bởi công thức \(h = 30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right)\). Sau bao nhiêu giây thì cabin đạt độ cao 40 m lần đầu tiên (viết kết quả ở dạng số thập phân)?
Đáp án:
Đáp án:
Giải phương trình \(30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right) = 40\) và tìm nghiệm t dương nhỏ nhất.
\(30 + 20\sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right) = 40 \Leftrightarrow \sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right) = \frac{1}{2} \Leftrightarrow \sin \left( {\frac{\pi }{{25}}t + \frac{\pi }{3}} \right) = \sin \frac{\pi }{6}\)
\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{25}}t + \frac{\pi }{3} = \frac{\pi }{6} + k2\pi \\\frac{\pi }{{25}}t + \frac{\pi }{3} = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{{25}}{6} + k50\\t = \frac{{25}}{2} + k50\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{{25}}{6} + k50\\t = \frac{{25}}{2} + k50\end{array} \right.\) \((k \in \mathbb{Z})\).
Ta thấy nghiệm dương nhỏ nhất là \(t = \frac{{25}}{2} = 12,5\) (giây) khi k = 0.
Vậy sau 12,5 giây thì cabin đạt độ cao 40m lần đầu tiên.
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá của mét khoan đầu tiên là 100 nghìn đồng và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 30 nghìn đồng so với giá của mét khoan ngay trước đó. Một người cần khoan một giếng sâu 20 m để lấy nước dùng cho sinh hoạt của gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bao nhiêu nghìn đồng?
Đáp án:
Đáp án:
Sử dụng công thức tổng n số hạng đầu của cấp số cộng: \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\).
Số tiền khoan mỗi mét lập thành một cấp số cộng với \({u_1} = 100\) và d = 30 (nghìn đồng).
Tổng số tiền cần để khoan 20m giếng là:
\({S_{20}} = \frac{{20.\left[ {2.100 + (20 - 1).30} \right]}}{2} = 7700\).
Vậy số tiền cần thanh toán là 7700 nghìn đồng.
Tìm công bội của cấp số nhân thỏa \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 135\\{u_4} + {u_5} + {u_6} = 40\end{array} \right.\).
Đáp án:
Đáp án:
Sử dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\).
\(\left\{ \begin{array}{l}{u_1} + {u_5} = 51\\{u_2} + {u_6} = 102\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + {u_1}{q^4} = 51\\{u_1}q + {u_1}{q^5} = 102\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}(1 + {q^4}) = 51\\{u_1}q(1 + {q^4}) = 102\end{array} \right. \Leftrightarrow q = \frac{{102}}{{51}} = 2\).
Suy ra \({u_1} = \frac{{51}}{{1 + {2^4}}} = 3\).
Vậy \({u_3} = {u_1}{q^2} = {3.2^2} = 12\).
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt x - 1}}{{{x^2} - 1}}\\{m^2}x\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\) liên tục tại điểm \({x_0} = 1\)?
Đáp án:
Đáp án:
Hàm số liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = \mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = f({x_0})\).
Ta có:
\(f(1) = {m^2}.1 = {m^2}\mathop {\lim }\limits_{x \to \infty } \).
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{{x^2} - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)\left( {x + 1} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\left( {\sqrt x + 1} \right)\left( {x + 1} \right)}} = \frac{1}{{\left( {\sqrt 1 + 1} \right)\left( {1 + 1} \right)}} = \frac{1}{4}\).
Để hàm số liên tục tại \({x_0} = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1) \Leftrightarrow {m^2} = \frac{1}{4} \Leftrightarrow m = \pm \frac{1}{2}\).
Vậy không có giá trị nguyên m nào để f(x) liên tục tại \({x_0} = 1\).
Cho tứ diện ABCD có I, J lần lượt là trung điểm của các cạnh BC và BD. Gọi (P) là mặt phẳng qua I, J và cắt hai cạnh AC và AD lần lượt tại M và N. Để IJNM là hình thoi thì AC = kAM và AB = mCD. Khi đó giá trị của k + m bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng tính chất đường trung bình, định lí Thales.
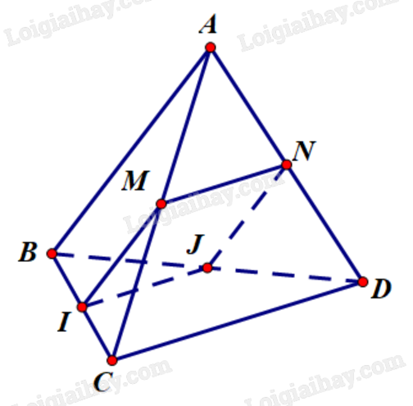
Vì IJ là đường trung bình của tam giác ABC nên IJ//CD và \(IJ = \frac{1}{2}CD\).
Để IJNM là hình thoi thì IJNM phải là hình bình hành và có NM = MI.
Để IJNM là hình bình hành thì cần MN//IJ và MN = IJ, hay MN//CD và \(MN = \frac{1}{2}CD\).
Khi đó, MN là đường trung bình tam giác ACD, tức M, N lần lượt là trung điểm của AC, AD.
Do đó AC = 2AM nên k = 2.
Ta cũng có MI là đường trung bình tam giác ABC nên \(MI = \frac{1}{2}AB\).
Để MN = MI thì AB = CD, suy ra m = 1.
Vậy k + m = 2 + 1 = 3.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng \(\left( \alpha \right)\) qua BD và song song với SA, mặt phẳng \(\left( \alpha \right)\) cắt SC tại K. Biết SK = mKC. Tính giá trị biểu thức \({m^2} + 2\).
Đáp án:
Đáp án:
Sử dụng điều kiện và tính chất của đường thẳng song song với mặt phẳng.
Sử dụng định lý Thales.
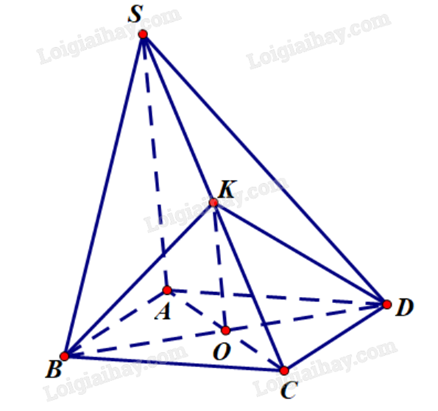
Mặt phẳng \(\left( \alpha \right)\) qua BD, cắt AC tại K nên mặt phẳng \(\left( \alpha \right)\) cũng là mặt phẳng (BKD).
Giả sử AC giao BD tại O. Khi đó O là trung điểm của AC, hay \(\frac{{OC}}{{AC}} = \frac{1}{2}\).
Vì \(O \in BD \subset (BKD)\) nên \(OK \subset (BKD)\).
Vì SA//(BKD) nên SA không cắt OK (1)
Mà \(\left\{ \begin{array}{l}O \in AC \subset (SAC)\\K \in SC \subset (SAC)\end{array} \right.\) suy ra \(OK \subset (SAC)\) (2)
Lại có \(SA \subset (SAC)\) (3)
Từ (1), (2), (3) suy ra SA//OK.
Xét tam giác SAC có OK//SA: \(\frac{{OC}}{{AC}} = \frac{{CK}}{{SC}} = \frac{1}{2}\) (định lí Thales).
Suy ra SK = KC, do đó m = 1.
Vậy \({m^2} + 2 = {1^2} + 2 = 3\).
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 9
Đề thi học kì 1 Toán 11 Cánh diều - Đề số 10
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm (6 điểm) Câu 1: Chọn đáp án đúng (với giả thiết các biểu thức đều có nghĩa).
Phần trắc nghiệm (6 điểm) Câu 1: Nghiệm của phương trình
Phần trắc nghiệm (6 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (6 điểm) Câu 1: Chọn đáp án đúng
Phần trắc nghiệm (6 điểm) Câu 1: Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là
A. Nội dung ôn tập Hàm số lượng giác và phương trình lượng giác 1. Góc lượng giác. Giá trị lượng giác của góc lượng giác 2. Các phép biến đổi lượng giác 3. Hàm số lượng giác và đồ thị 4. Phương trình lượng giác cơ bản
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận