Đề thi học kì 2 Toán 11 Cánh diều - Đề số 9
Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Rút gọn biểu thức \(P = {x^{\frac{2}{5}}}.\sqrt[6]{x}\) với x > 0.
-
A.
\(P = \sqrt x \)
-
B.
\(P = {x^{\frac{{17}}{{30}}}}\)
-
C.
\(P = {x^{\frac{1}{{15}}}}\)
-
D.
\(P = {x^{\frac{{17}}{{15}}}}\)
Cho a > 0 và \(a \ne 1\), khi đó \({\log _a}\sqrt[3]{a}\) bằng
-
A.
\( - \frac{1}{3}\)
-
B.
\(\frac{1}{3}\)
-
C.
\(-3\)
-
D.
\(3\)
Tập xác định của hàm số \(y = {\log _5}x\) là
-
A.
\(\left( { - \infty ; + \infty } \right)\)
-
B.
\(\left[ {0; + \infty } \right)\)
-
C.
\(\left( { - \infty ;0} \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Cho mẫu số liệu ghép nhóm của chiều cao của cây cao su trong một nông trường:
Trung vị của mẫu số liệu trên là
-
A.
\(\frac{{1121}}{{60}}\)
-
B.
\(\frac{{75}}{4}\)
-
C.
\(\frac{{1127}}{{60}}\)
-
D.
\(\frac{{1123}}{{60}}\)
Hàm số \(y = {x^2} + x + 1\) có đạo hàm trên \(\mathbb{R}\) là
-
A.
\(y' = 3x\)
-
B.
\(y' = 2 + x\)
-
C.
\(y' = {x^2} + x\)
-
D.
\(y' = 2x + 1\)
Đạo hàm của hàm số \(y = {5^x}\) là
-
A.
\(y' = - {5^x}\ln 5\)
-
B.
\(y' = \frac{{{5^x}}}{{\ln 5}}\)
-
C.
\(y' = {5^x}\ln 5\)
-
D.
\(y' = \frac{{ - {5^x}}}{{\ln 5}}\)
Hệ số góc của tiếp tuyến với đồ thị hàm số \(y = f(x) = {x^2}\) tại điểm có hoành độ \({x_0} = - 2\) là
-
A.
-4
-
B.
4
-
C.
2
-
D.
-2
Gieo một con xúc xắc cân đối và đồng chất một lần. Gọi A biến cố “Số chấm xuất hiện của con xúc xắc là số chẵn”. Biến cố A xung khắc với biến cố nào sau đây?
-
A.
“Số chấm xuất hiện của con xúc xắc là số lẻ”
-
B.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 3”
-
C.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 6”
-
D.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 4”
Cho A và B là hai biến cố độc lập với nhau. P(A) = 0,4, P(B) = 0,3. Khi đó P(AB) bằng
-
A.
0,1
-
B.
0,58
-
C.
0,7
-
D.
0,12
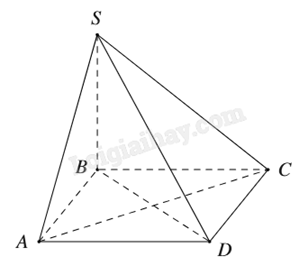
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SCD)\)
-
B.
\(AC \bot (SBD)\)
-
C.
\(AC \bot (SBC)\)
-
D.
\(AC \bot (SAB)\)
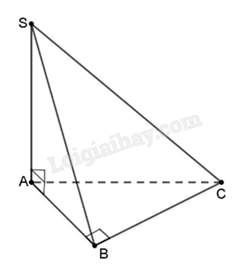
Cho hình chóp S.ABC, đáy là tam giác ABC vuông tại B, cạnh \(SA \bot (ABC)\). Chọn khẳng định đúng.
-
A.
\(d\left( {C,(SAB)} \right) = CS\)
-
B.
\(d\left( {A,(SBC)} \right) = AB\)
-
C.
\(d\left( {C,(SAB)} \right) = CB\)
-
D.
\(d\left( {S,(SBC)} \right) = SA\)
Khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \) và chiều cao bằng \(2a\sqrt 3 \). Thể tích khối lăng trụ đã cho bằng
-
A.
\(3{a^3}\)
-
B.
\(2{a^3}\)
-
C.
\(6{a^3}\)
-
D.
\(2{a^3}\sqrt 3 \)
Một chất điểm chuyển động trong 60 giây đầu tiên có phương trình \(s(t) = \frac{1}{{12}}{t^4} - \frac{2}{3}{t^3} + 6{t^2} + 7t\), trong đó t > 0 và tính bằng giây (s), s(t) tính bằng mét (m).
a) Vận tốc chuyển động \(v(t) = \frac{1}{3}{t^3} + 2{t^2} + 12t + 7\).
b) Gia tốc chuyển động \(a(t) = v'(t) = {t^2} - 4t + 12\).
c) Tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng \(\frac{{77}}{3}\) m/s.
d) Vận tốc chuyển động tại thời điểm t = 1 là \(v(t) = \frac{{32}}{3}\) m/s.
Gieo hai đồng xu A và B một cách độc lập. Đồng xu A được chế tạo cân đối. Đồng xu B được chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa.
a) Xác suất đồng xu A xuất hiện mặt ngửa bằng \(\frac{1}{2}\).
b) Xác suất đồng xu B xuất hiện mặt ngửa bằng \(\frac{1}{4}\).
c) Khi gieo hai đồng xu một lần thì xác suất cả hai đều ngửa bằng \(\frac{1}{{12}}\).
d) Khi gieo hai đồng xu hai lần thì xác suất cả hai đồng xu đều ngửa bằng \(\frac{1}{{32}}\).
Một người lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ trước được cộng vào vốn của kỳ kế tiếp) với kì hạn 3 tháng, lãi suất 2% một quý. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi tiền vào ngân hàng bằng bao nhiêu triệu đồng? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra.
Hai đội công nhân trong một nhà máy sản xuất có xác suất tạo ra sản phẩm tốt lần lượt là 0,75 và 0,85. Tính xác suất phế phẩm mà nhà máy đó tạo ra bởi cả hai đội (kết quả làm tròn tới hàng phần trăm).
Cho hàm số \(f(x) = {x^2}{e^{ - 2x}}\). Tính tổng các nghiệm của phương trình \(f'(x) = 0\).
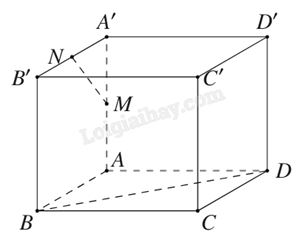
Công ty sản xuất đồ chơi Electric X giao cho nhân viên thiết kế một mô hình khối hình hộp ABCD.A’B’C’ D’ có 6 mặt là hình vuông cạnh bằng 2024 (cm) như hình vẽ. Giả sử M, N lần lượt là trung điểm của cạnh AA′ và A′ B′. Để ghi các thông số kĩ thuật thì công ty yêu cầu nhân viên tính số đo góc giữa hai đường thẳng MN và BD trước khi sản xuất hàng loạt. Hỏi số đo góc giữa hai đường thẳng MN và BD là bao nhiêu độ?
Lời giải và đáp án
Rút gọn biểu thức \(P = {x^{\frac{2}{5}}}.\sqrt[6]{x}\) với x > 0.
-
A.
\(P = \sqrt x \)
-
B.
\(P = {x^{\frac{{17}}{{30}}}}\)
-
C.
\(P = {x^{\frac{1}{{15}}}}\)
-
D.
\(P = {x^{\frac{{17}}{{15}}}}\)
Đáp án : B
Áp dụng công thức \({x^a}.{x^b} = {x^{a + b}}\) và \(\sqrt[b]{{{x^a}}} = {x^{\frac{a}{b}}}\).
\(P = {x^{\frac{2}{5}}}.\sqrt[6]{x} = {x^{\frac{2}{5}}}.{x^{\frac{1}{6}}} = {x^{\frac{2}{5} + \frac{1}{6}}} = {x^{\frac{{17}}{{30}}}}\).
Cho a > 0 và \(a \ne 1\), khi đó \({\log _a}\sqrt[3]{a}\) bằng
-
A.
\( - \frac{1}{3}\)
-
B.
\(\frac{1}{3}\)
-
C.
\(-3\)
-
D.
\(3\)
Đáp án : B
Áp dụng công thức \(\sqrt[b]{{{x^a}}} = {x^{\frac{a}{b}}}\) và \({\log _x}{x^\alpha } = \alpha \).
\({\log _a}\sqrt[3]{a} = {\log _a}{a^{\frac{1}{3}}} = \frac{1}{3}\).
Tập xác định của hàm số \(y = {\log _5}x\) là
-
A.
\(\left( { - \infty ; + \infty } \right)\)
-
B.
\(\left[ {0; + \infty } \right)\)
-
C.
\(\left( { - \infty ;0} \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Đáp án : D
Áp dụng lí thuyết về tập xác định của hàm số logarit.
Tập xác định của hàm số \(y = {\log _5}x\) là \(\left( {0; + \infty } \right)\).
Cho mẫu số liệu ghép nhóm của chiều cao của cây cao su trong một nông trường:
Trung vị của mẫu số liệu trên là
-
A.
\(\frac{{1121}}{{60}}\)
-
B.
\(\frac{{75}}{4}\)
-
C.
\(\frac{{1127}}{{60}}\)
-
D.
\(\frac{{1123}}{{60}}\)
Đáp án : D
Tìm cỡ mẫu rồi áp dụng công thức tính trung vị của mẫu số liệu ghép nhóm.
Ta có: \(n = 55 + 78 + 120 + 45 + 11 = 309\).
Trung vị: \({Q_2} = {x_{155}} \in \left[ {18;22} \right)\): \({Q_2} = 18 + \left( {22 - 18} \right).\frac{{\frac{{309.2}}{4} - 55 - 78}}{{120}} = \frac{{1123}}{{60}}\).
Hàm số \(y = {x^2} + x + 1\) có đạo hàm trên \(\mathbb{R}\) là
-
A.
\(y' = 3x\)
-
B.
\(y' = 2 + x\)
-
C.
\(y' = {x^2} + x\)
-
D.
\(y' = 2x + 1\)
Đáp án : D
Áp dụng công thức \(\left( {{x^\alpha }} \right)' = \alpha .{x^{\alpha - 1}}\).
\(y' = \left( {{x^2} + x + 1} \right)' = 2x + 1\).
Đạo hàm của hàm số \(y = {5^x}\) là
-
A.
\(y' = - {5^x}\ln 5\)
-
B.
\(y' = \frac{{{5^x}}}{{\ln 5}}\)
-
C.
\(y' = {5^x}\ln 5\)
-
D.
\(y' = \frac{{ - {5^x}}}{{\ln 5}}\)
Đáp án : C
Áp dụng công thức đạo hàm \(\left( {{a^x}} \right)' = {a^x}\ln a\).
\(y' = \left( {{5^x}} \right)' = {5^x}\ln 5\).
Hệ số góc của tiếp tuyến với đồ thị hàm số \(y = f(x) = {x^2}\) tại điểm có hoành độ \({x_0} = - 2\) là
-
A.
-4
-
B.
4
-
C.
2
-
D.
-2
Đáp án : B
Tính f’(2).
\(f'(x) = \left( {{x^2}} \right)' = 2x\).
Hệ số góc của tiếp tuyến là f’(2) = 2.2 = 4.
Gieo một con xúc xắc cân đối và đồng chất một lần. Gọi A biến cố “Số chấm xuất hiện của con xúc xắc là số chẵn”. Biến cố A xung khắc với biến cố nào sau đây?
-
A.
“Số chấm xuất hiện của con xúc xắc là số lẻ”
-
B.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 3”
-
C.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 6”
-
D.
“Số chấm xuất hiện của con xúc xắc là số chia hết cho 4”
Đáp án : A
Hai biến cố được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.
Biến cố xung khắc của A là “Số chấm xuất hiện của con xúc xắc là số lẻ”.
Cho A và B là hai biến cố độc lập với nhau. P(A) = 0,4, P(B) = 0,3. Khi đó P(AB) bằng
-
A.
0,1
-
B.
0,58
-
C.
0,7
-
D.
0,12
Đáp án : D
Áp dụng quy tắc nhân xác suất cho hai biến cố độc lập: P(AB) = P(A).P(B).
Vì A và B là hai biến cố độc lập nên P(AB) = P(A).P(B) = 0,4.0,3 = 0,12.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SCD)\)
-
B.
\(AC \bot (SBD)\)
-
C.
\(AC \bot (SBC)\)
-
D.
\(AC \bot (SAB)\)
Đáp án : B
Đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
Vì ABCD là hình vuông nên \(AC \bot BD\).
Mặt khác \(SB \bot (ABCD)\) nên \(SB \bot AC\).
Do đó \(AC \bot (SBD)\).
Cho hình chóp S.ABC, đáy là tam giác ABC vuông tại B, cạnh \(SA \bot (ABC)\). Chọn khẳng định đúng.
-
A.
\(d\left( {C,(SAB)} \right) = CS\)
-
B.
\(d\left( {A,(SBC)} \right) = AB\)
-
C.
\(d\left( {C,(SAB)} \right) = CB\)
-
D.
\(d\left( {S,(SBC)} \right) = SA\)
Đáp án : C
Khoảng cách từ một điểm tới một mặt phẳng là khoảng cách từ điểm đó đến hình chiếu của nó trên mặt phẳng.
Ta có: \(d\left( {C,(SAB)} \right) = CB\);
\(d\left( {A,(SBC)} \right)\) là khoảng cách từ A đến chân đường vuông góc hạ xuống SB;
\(d\left( {S,(SBC)} \right) = 0\).
Khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \) và chiều cao bằng \(2a\sqrt 3 \). Thể tích khối lăng trụ đã cho bằng
-
A.
\(3{a^3}\)
-
B.
\(2{a^3}\)
-
C.
\(6{a^3}\)
-
D.
\(2{a^3}\sqrt 3 \)
Đáp án : C
Áp dụng công thức tính thể tích khối lăng trụ V = Bh.
\(V = Bh = {a^2}\sqrt 3 .2a\sqrt 3 = 6{a^3}\).
Một chất điểm chuyển động trong 60 giây đầu tiên có phương trình \(s(t) = \frac{1}{{12}}{t^4} - \frac{2}{3}{t^3} + 6{t^2} + 7t\), trong đó t > 0 và tính bằng giây (s), s(t) tính bằng mét (m).
a) Vận tốc chuyển động \(v(t) = \frac{1}{3}{t^3} + 2{t^2} + 12t + 7\).
b) Gia tốc chuyển động \(a(t) = v'(t) = {t^2} - 4t + 12\).
c) Tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng \(\frac{{77}}{3}\) m/s.
d) Vận tốc chuyển động tại thời điểm t = 1 là \(v(t) = \frac{{32}}{3}\) m/s.
a) Vận tốc chuyển động \(v(t) = \frac{1}{3}{t^3} + 2{t^2} + 12t + 7\).
b) Gia tốc chuyển động \(a(t) = v'(t) = {t^2} - 4t + 12\).
c) Tại thời điểm gia tốc của vật đạt giá trị nhỏ nhất thì vận tốc của vật bằng \(\frac{{77}}{3}\) m/s.
d) Vận tốc chuyển động tại thời điểm t = 1 là \(v(t) = \frac{{32}}{3}\) m/s.
a) v(t) = s’(t).
b) a(t) = v’(t).
c) Tìm \({t_0}\) sao cho gia tốc nhỏ nhất. Tính \(v({t_0})\).
d) Tính v(1).
a) Sai. \(v(t) = s'(t) = \frac{1}{3}{t^3} - 2{t^2} + 12t + 7\).
b) Đúng. \(a(t) = v'(t) = {t^2} - 4t + 12\).
c) Đúng. Gia tốc của vật đạt giá trị nhỏ nhất tại \(t = - \frac{{ - 4}}{{2.1}} = 2\).
Khi đó \(v(2) = \frac{1}{3}{.2^3} - {2.2^2} + 12.2 + 7 = \frac{{77}}{3}\) (m/s).
d) Sai. \(v(1) = \frac{1}{3}{.1^3} - {2.1^2} + 12.1 + 7 = \frac{{52}}{3}\) (m/s).
Gieo hai đồng xu A và B một cách độc lập. Đồng xu A được chế tạo cân đối. Đồng xu B được chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa.
a) Xác suất đồng xu A xuất hiện mặt ngửa bằng \(\frac{1}{2}\).
b) Xác suất đồng xu B xuất hiện mặt ngửa bằng \(\frac{1}{4}\).
c) Khi gieo hai đồng xu một lần thì xác suất cả hai đều ngửa bằng \(\frac{1}{{12}}\).
d) Khi gieo hai đồng xu hai lần thì xác suất cả hai đồng xu đều ngửa bằng \(\frac{1}{{32}}\).
a) Xác suất đồng xu A xuất hiện mặt ngửa bằng \(\frac{1}{2}\).
b) Xác suất đồng xu B xuất hiện mặt ngửa bằng \(\frac{1}{4}\).
c) Khi gieo hai đồng xu một lần thì xác suất cả hai đều ngửa bằng \(\frac{1}{{12}}\).
d) Khi gieo hai đồng xu hai lần thì xác suất cả hai đồng xu đều ngửa bằng \(\frac{1}{{32}}\).
Áp dụng quy tắc nhân xác suất và tính xác suất của biến cố đối.
a) Đúng. Xác suất đồng xu A ngửa bằng \(\frac{1}{2}\).
b) Đúng. Xác suất đồng xu B ngửa là x, xác suất đồng xu B sấp là 1 – x.
Vì xác suất xuất hiện mặt sấp gấp 3 lần xác suất xuất hiện mặt ngửa nên ta có \(1 - x = 3x\), suy ra \(x = \frac{1}{4}\).
Vậy xác suất đồng xu B ngửa bằng \(\frac{1}{4}\).
c) Sai. Xác suất cả hai đồng xu đều ngửa là \(\frac{1}{2}.\frac{1}{4} = \frac{1}{8}\).
d) Sai. Xác suất cả hai đồng xu đều ngửa khi tung hai lần là \({\left( {\frac{1}{2}} \right)^2}.{\left( {\frac{1}{4}} \right)^2} = \frac{1}{{64}}\).
Một người lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ trước được cộng vào vốn của kỳ kế tiếp) với kì hạn 3 tháng, lãi suất 2% một quý. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi tiền vào ngân hàng bằng bao nhiêu triệu đồng? Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra.
- Tính số tiền có được sau 6 tháng đầu.
- Tính số tiền có được sau 1 năm gửi tiếp.
Sử dụng công thức lãi kép không kì hạn \(T = A{\left( {1 + r} \right)^N}\).
Số tiền người đó có sau 6 tháng = 2 quý: \({T_1} = 100{\left( {1 + 2\% } \right)^2} = 104,04\) triệu đồng.
Số tiền người đó có ngay sau khi gửi thêm 100 triệu là: \(104,04 + 100 = 204,04\) triệu đồng.
Số tiền người đó có sau 1 năm = 4 quý nữa là: \({T_2} = 204,04{\left( {1 + 2\% } \right)^4} \approx 220\) triệu đồng.
Hai đội công nhân trong một nhà máy sản xuất có xác suất tạo ra sản phẩm tốt lần lượt là 0,75 và 0,85. Tính xác suất phế phẩm mà nhà máy đó tạo ra bởi cả hai đội (kết quả làm tròn tới hàng phần trăm).
Áp dụng quy tắc nhân và tính xác suất của biến cố đối.
Xác suất phế phẩm mà nhà máy đó tạo ra bởi cả hai đội là \((1 - 0,75)(1 - 0,85) = 0,0375 \approx 0,04\).
Cho hàm số \(f(x) = {x^2}{e^{ - 2x}}\). Tính tổng các nghiệm của phương trình \(f'(x) = 0\).
Tìm TXĐ. Tính f’(x) và giải phương trình f’(x) = 0.
TXĐ: \(D = \mathbb{R}\).
\(f'(x) = \left( {{x^2}} \right)'{e^{ - 2x}} + {x^2}\left( {{e^{ - 2x}}} \right)' \)
\(= 2x{e^{ - 2x}} - 2{x^2}{e^{ - 2x}} = 2x{e^{ - 2x}}(1 - x)\).
\(f'(x) = 0 \Leftrightarrow 2x{e^{ - 2x}}(1 - x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy tổng các nghiệm của phương trình f’(x) = 0 là 0 + 1 = 1.
Công ty sản xuất đồ chơi Electric X giao cho nhân viên thiết kế một mô hình khối hình hộp ABCD.A’B’C’ D’ có 6 mặt là hình vuông cạnh bằng 2024 (cm) như hình vẽ. Giả sử M, N lần lượt là trung điểm của cạnh AA′ và A′ B′. Để ghi các thông số kĩ thuật thì công ty yêu cầu nhân viên tính số đo góc giữa hai đường thẳng MN và BD trước khi sản xuất hàng loạt. Hỏi số đo góc giữa hai đường thẳng MN và BD là bao nhiêu độ?
Gọi P là trung điểm của A’D’.
Tính \((MN,BD) = (MN,NP) = \widehat {MNP}\).
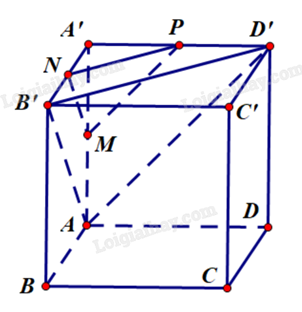
Gọi P là trung điểm của A’D’.
Dễ thấy NP // B’D’ // BD. Do đó, \((MN,BD) = (MN,NP) = \widehat {MNP}\).
Ta có độ dài đường chéo các mặt của khối lập phương là \(AB' = AD' = B'D' = 2024\sqrt 2 \).
Vì MN là đường trung bình tam giác A’B’A nên \(MN = \frac{{AB'}}{2} = \frac{{2024\sqrt 2 }}{2} = 1012\sqrt 2 \).
Tương tự, ta có \(NP = MP = 1012\sqrt 2 \).
Do đó, tam giác MNP là tam giác đều, suy ra \(\widehat {MNP} = {60^o}\).
Vậy góc giữa MN và BD bằng \({60^o}\).
Lập phương trình hoành độ giao điểm của (C) và d, giải tìm nghiệm \({x_0}\).
Phương trình tiếp tuyến của f(x) tại \({x_0}\) là \(y = f'({x_0})(x - {x_0}) + {y_0}\).
Ta có: \(y' = \left( {\frac{{x - 2}}{{2x + 1}}} \right)' = \frac{{\left( {x - 2} \right)'\left( {2x + 1} \right) - \left( {x - 2} \right)\left( {2x + 1} \right)'}}{{{{\left( {2x + 1} \right)}^2}}}\)
\( = \frac{{1.\left( {2x + 1} \right) - \left( {x - 2} \right).2}}{{{{\left( {2x + 1} \right)}^2}}} = \frac{{2x + 1 - 2x + 4}}{{{{\left( {2x + 1} \right)}^2}}} = \frac{5}{{{{\left( {2x + 1} \right)}^2}}}\).
Phương trình hoành độ giao điểm của d và (C) là \(\frac{{x - 2}}{{2x + 1}} = x - 2 \Leftrightarrow \left( {2x + 1} \right)\left( {x - 2} \right) = x - 2 \Leftrightarrow 2{x^2} - 4x = 0 \Leftrightarrow 2x\left( {x - 2} \right) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = 2\).
Với \({x_0} = 2\), ta có \(y'({x_0}) = y'(2) = \frac{5}{{{{\left( {2.2 + 1} \right)}^2}}} = \frac{1}{5}\); \(y({x_0}) = y(2) = \frac{{2 - 2}}{{2.2 + 1}} = 0\).
Phương trình tiếp tuyến là \(y = \frac{1}{5}(x - 2) + 0 \Leftrightarrow y = \frac{1}{5}x - \frac{2}{5}\).
Với \({x_0} = 0\), ta có \(y'({x_0}) = y'(0) = \frac{5}{{{{\left( {2.0 + 1} \right)}^2}}} = 5\); \(y({x_0}) = y(0) = \frac{{0 - 2}}{{2.0 + 1}} = - 2\).
Phương trình tiếp tuyến là \(y = 5(x - 0) - 2 \Leftrightarrow y = 5x - 2\).
Tìm ĐKXĐ và giải bất phương trình.
ĐKXĐ: \(\left\{ \begin{array}{l}{\log _2}\left( {2 - {x^2}} \right) > 0\\2 - {x^2} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 - {x^2} > {2^0}\\{x^2} < 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} < 1\\{x^2} < 2\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l} - 1 < x < 1\\ - 2 < x < 2\end{array} \right. \Leftrightarrow - 1 < x < 1\).
Khi đó \({\log _{\frac{1}{2}}}\left[ {{{\log }_2}\left( {2 - {x^2}} \right)} \right] > 0 \Leftrightarrow {\log _2}\left( {2 - {x^2}} \right) < {\left( {\frac{1}{2}} \right)^0} \Leftrightarrow {\log _2}\left( {2 - {x^2}} \right) < 1\)
\( \Leftrightarrow 2 - {x^2} < {2^1} \Leftrightarrow {x^2} > 0 \Leftrightarrow x \ne 0\).
Kết hợp ĐK, ta có tập nghiệm của bất phương trình là \(S = \left( { - 1;0} \right) \cup \left( {0;1} \right)\).
Xác định đoạn thẳng thể hiện khoảng cách giữa AB và SC. Từ đó, áp dụng hệ thức lượng trong tam giác vuông để tìm chiều cao khối chóp và tính thể tích.
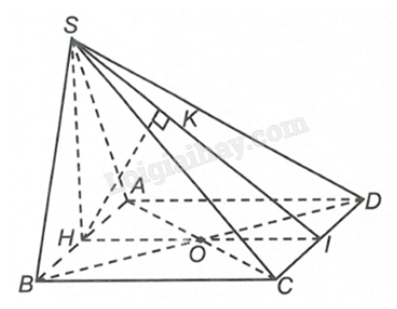
Gọi H, I lần lượt là trung điểm của AB, CD. Kẻ \(HK \bot SI\).
SH vừa là đường cao, vừa là đường trung tuyến của tam giác cân SAB, suy ra \(SH \bot AB\).
Mà \((SAB) \bot (ABCD)\), \((SAB) \cap (ABCD) = AB\) nên \(SH \bot (ABCD) \Rightarrow SH \bot CD\).
Ta có \(\left\{ \begin{array}{l}SH \bot CD\\HI \bot CD\end{array} \right. \Rightarrow CD \bot (SHI) \Rightarrow CD \bot HK\).
Mặt khác \(\left\{ \begin{array}{l}HK \bot SI\\HK \bot CD\end{array} \right. \Rightarrow HK \bot (SCD)\).
Vì CD // AB nên \(d\left( {AB,DC} \right) = d\left( {AB,(SCD)} \right) = d\left( {H,(SCD)} \right) = HK\).
Ta có \(HK = \frac{3}{2}\), \(HI = AD = \sqrt 3 \).
Xét tam giác vuông SHI vuông tại H có đường cao HK:
\(\frac{1}{{H{K^2}}} = \frac{1}{{H{S^2}}} + \frac{1}{{H{I^2}}} \Leftrightarrow \frac{1}{{H{S^2}}} = \frac{1}{{H{K^2}}} - \frac{1}{{H{I^2}}} = \frac{1}{{{{\left( {\frac{3}{2}} \right)}^2}}} - \frac{1}{{{{\left( {\sqrt 3 } \right)}^2}}} = \frac{1}{9} \Leftrightarrow HS = 3\).
Thể tích khối chóp là \({V_{S.ABCD}} = \frac{1}{3}.SH.{S_{ACBD}} = \frac{1}{3}.SH.AB.AD = \frac{1}{3}.3.1.\sqrt 3 = \sqrt 3 \approx 1,73\).
Câu 1: Với b,c là hai số thực dương tùy ý thỏa mãn ({rm{lo}}{{rm{g}}_5}b ge {rm{lo}}{{rm{g}}_5}c), khẳng định nào dưới đây là đúng? A. (b ge c). B. (b le c). C. (b > c). D. (b < c).
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP 1. Một số yếu tố thống kê và xác suất - Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm - Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất 2. Hàm số mũ và hàm số logarit - Phép tính lũy thừa với số mũ thực - Phép tính logarit - Hàm số mũ và hàm số logarit - Phương trình, bất phương trình mũ và logarit
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
