 Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi học kì 1 Toán 7 Kết nối tri thức
Đề thi học kì 1 Toán 7 Kết nối tri thức Đề thi học kì 1 Toán 7 - Đề số 6 - Kết nối tri thức
Tải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Chọn phương án đúng?
A. \(\dfrac{1}{2} \notin \mathbb{Q}\)
B. \(\dfrac{{ - 8}}{0} \in \mathbb{Q}\)
C. \(5 \notin \mathbb{Q}\)
D. \(\dfrac{4}{{ - 5}} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\) là:
A. \({\left( {0,3} \right)^4}\)
B. \({\left( {0,3} \right)^{10}}\)
C. \({\left( {0,3} \right)^{15}}\)
D. \({\left( {0,3} \right)^{12}}\)
Câu 3: Sắp xếp các số sau theo thứ tự tăng dần: \(2\dfrac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
A. \(2\dfrac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
B. \(\sqrt {16} \,\,;\,\,2\dfrac{1}{4}\,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,\,\, - \sqrt {83} \,\,;\, - \left| { - \sqrt {196} } \right|\,.\)
C. \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\dfrac{1}{4}\,\,;\,\,\sqrt {16} .\)
D. \(\sqrt {16} \,\,;\,\,2\dfrac{1}{4}\,\,;\,\,\, - 0,0\left( {51} \right)\,\,;\,\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,.\)
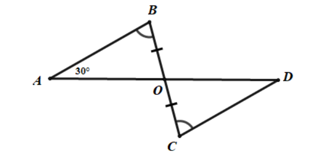
Câu 4: Cho hình vẽ sau. Tính số đo \(\angle D\)?
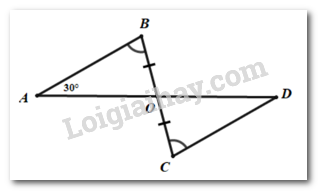
A. \(100^\circ \)
B. \(50^\circ \)
C. \(30^\circ \)
D. \(70^\circ \)
Câu 5: Tam giác \(ABC\) có \(\angle A = {75^0};\angle B - \angle C = {25^0}\). Tính \(\angle C\)?
A. \(\angle C = {40^0}\)
B. \(\angle C = {65^0}\)
C. \(\angle C = {35^0}\)
D. \(\angle C = {45^0}\)
Câu 6: Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
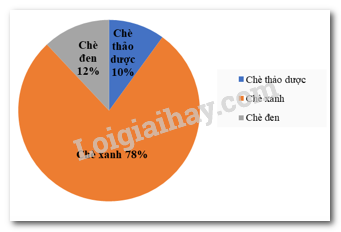
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
Câu 7: Cho biểu đồ sau:
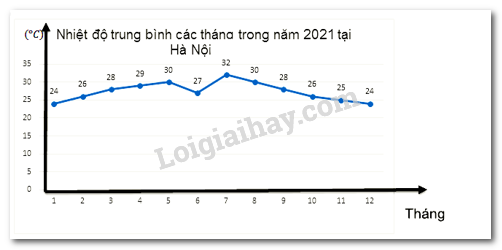
Hãy cho biết tiêu chí thống kê của biểu đồ trên là gì?
A. Tháng 1 đến tháng 12
B. Nhiệt độ trung bình các tháng trong năm 2021 tại Hà Nội
C. Nhiệt độ trung bình tại Hà Nội năm 2021 thay đổi theo thời gian
D. Nhiệt độ
Câu 8: Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = AC\). Qua \(A\) kẻ đường thẳng \(d\) cắt \(BC\). Vẽ \(BM,CN\) vuông góc với \(d\) với \(M,N \in d\). Chọn đáp án sai:
A. \(AM = CN\)
B. \(BM = AN\)
C. \(\angle ABM = \angle ACN\)
D.\(\angle ABM = \angle CAN\)
Câu 9: Hai góc nào dưới đây là hai góc đối đỉnh?
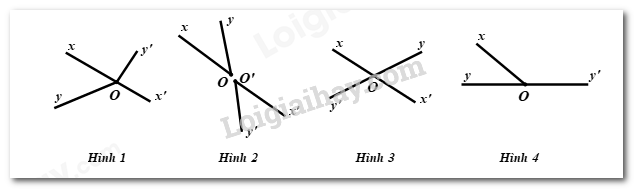
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
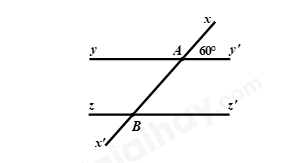
Câu 10: Cho hình vẽ bên dưới, biết \(yy'//zz',\angle xAy' = {60^0}\). Tính số đo của \(\angle zBx'.\)
A. \(\angle zBx' = {120^0}\)
B. \(\angle zBx' = {80^0}\)
C. \(\angle zBx' = {50^0}\)
D. \(\angle zBx' = {60^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (1,5 điểm)
Thực hiện phép tính:
a) \(\left( {2\dfrac{5}{6} + 1\dfrac{4}{9}} \right):\left( {10\dfrac{1}{{12}} - 9,5} \right)\)
b) \(\dfrac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\dfrac{{25}}{{16}}} \)
d) \(\left| {\dfrac{1}{{ - 5}}} \right| - \dfrac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \dfrac{{\left| 2 \right|}}{5}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(x - \dfrac{1}{2} = 3\dfrac{1}{2}:\dfrac{2}{7}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
c) \(\sqrt {1,96} + 3\dfrac{x}{4} = \sqrt {0,04} + \dfrac{1}{4}.\sqrt {{{\left( {\dfrac{{89}}{5}} \right)}^2}} \)
d) \(\left| {2x:\dfrac{4}{5} - \dfrac{{1,6}}{4}} \right| = \dfrac{7}{5}\)
Bài 3: (3 điểm)
Cho tam giác \(ABC\) có : \(AB = AC\) và \(M\) là trung điểm của \(BC\).
a) Chứng minh \(AM\) là tia phân giác của góc \(BAC\).
b) Chứng minh \(AM \bot BC\).
c) Qua \(C\) kẻ đường thẳng \(d\) song song với \(AB\) cắt tia \(AM\) tại \(N\). Chứng minh \(M\) là trung điểm của \(AN\).
Bài 4: (0,5 điểm)
Tìm số nguyên \(x\) sao cho biểu thức sau là số nguyên:
\(G = \dfrac{{\sqrt x + 5}}{{\sqrt x - 3}}\)
Lời giải
Phần I: Trắc nghiệm
|
1.D |
2.C |
3.C |
4.C |
5.A |
6.B |
7.D |
8.C |
9.C |
10.D |
Câu 1
Phương pháp:
Số hữu tỉ là số viết được dưới dạng phân số \(\dfrac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).
Tập hợp các số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Cách giải:
Ta có:
+ \(\dfrac{1}{2} \in \mathbb{Q}\) nên phương án A. \(\dfrac{1}{2} \notin \mathbb{Q}\) là sai do đó, loại đáp án A.
+ \(\dfrac{{ - 8}}{0}\) không đúng với dạng số hữu tỉ (do mẫu số bằng \(0\)) nên phương án B. \(\dfrac{{ - 8}}{0} \in \mathbb{Q}\) là sai do đó, loại đáp án B.
+ \(5 = \dfrac{5}{1}\) là một số hữu tỉ và \(5 \in \mathbb{Q}\) nên phương án C. \(5 \notin \mathbb{Q}\) là sai do đó, loại đáp án C.
+ \(\dfrac{4}{{ - 5}}\) là một số hữu tỉ nên \(\dfrac{4}{{ - 5}} \in \mathbb{Q}\) do đó, phương án D đúng.
Chọn D.
Câu 2
Phương pháp:
Tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính tích của hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
Cách giải:
\({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\)\( = {\left( {0,3} \right)^{3.4}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12}}.{\left( {0,3} \right)^3} = {\left( {0,3} \right)^{12 + 3}} = {\left( {0,3} \right)^{15}}\)
Chọn C.
Câu 3
Phương pháp:
Đổi hỗn số sang phân số, từ phân số đổi sang số thập phân.
Tính căn bậc hai của một số.
Tính giá trị tuyệt đối của một số.
So sánh các số để sắp xếp thứ tự tăng dần của các số.
Cách giải:
Ta có:
\(\begin{array}{l}2\dfrac{1}{4} = \dfrac{9}{4} = 2,25\\\sqrt {16} = \sqrt {{4^2}} = 4\\ - \left| { - \sqrt {196} } \right| = - \left| {\sqrt {196} } \right| = - \sqrt {196} \end{array}\)
*Vì \(2,25 < 4\) nên \(2\dfrac{1}{4} < \sqrt {16} \) (*)
*Vì \(83 < 196\) nên \(\sqrt {83} < \sqrt {196} \) suy ra \( - \sqrt {83} > - \sqrt {196} \) hay \( - \sqrt {83} > - \left| { - \sqrt {196} } \right|\) (1)
Vì \(0,0\left( {51} \right) < 1 = \sqrt 1 < \sqrt {83} \) suy ra \( - \sqrt {83} < - 1 < - 0,0\left( {51} \right)\) (2)
Từ (1) và (2), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right)\) (**)
Từ (*) và (**), suy ra \( - \left| { - \sqrt {196} } \right| < - \sqrt {83} < - 0,0\left( {51} \right) < 2\dfrac{1}{4} < \sqrt {16} \)
Vậy thứ tự tăng dần của các số là: \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\dfrac{1}{4}\,\,;\,\,\sqrt {16} .\)
Chọn C.
Câu 4
Phương pháp:
+ Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
+ Hai tam giác bằng nhau có các cặp cạnh, cặp góc tương ứng bằng nhau
Cách giải:
Xét \(\Delta OAB\) và \(\Delta ODC\)có:
\(\angle ABO = \angle DCO\) (gt)
\(BO = DO\,\)(gt)
\(\angle AOB = \angle COD\,\)(đối đỉnh)
Vậy \(\Delta OAB = \Delta ODC\,\)(g.c.g)
\( \Rightarrow \,\angle D = \angle A = 30^\circ \)( 2 góc tương ứng)
Chọn C.
Câu 5
Phương pháp:
Vận dụng định lý: Tổng ba góc trong một tam giác bằng \({180^0}\).
Cách giải:
* Ta có: \(\angle B - \angle C = {25^0} \Rightarrow \angle B = \angle C + {25^0}\)
Xét \(\Delta ABC\) có: \(\angle A + \angle B + \angle C = {180^0}\) (định lí tổng ba góc trong tam giác)
\(\begin{array}{l} \Rightarrow {75^0} + \angle B + \angle C = {180^0}\\ \Rightarrow \angle B + \angle C = {180^0} - {75^0}\\ \Rightarrow \angle B + \angle C = {105^0}\\ \Rightarrow \angle C + {25^0} + \angle C = {105^0}\\ \Rightarrow 2\angle C + {25^0} = {105^0}\\ \Rightarrow 2\angle C = {105^0} - {25^0}\\ \Rightarrow 2\angle C = {80^0}\\ \Rightarrow \angle C = {80^0}:2\\ \Rightarrow \angle C = {40^0}\end{array}\)
Vậy \(\angle C = {40^0}\)
Chọn A.
Câu 6
Phương pháp:
Đọc và mô tả dữ liệu của biểu đồ hình quạt tròn.
Số tiền thu được tương ứng = % tương ứng . toàn bộ số tiền thu được
Cách giải:
Số tiền công ty Phú Minh thu được từ chè thảo dược là: \(10\% .25 = 2,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè xanh là: \(78\% .25 = 19,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè đen là: \(12\% .25 = 3\) (tỉ đồng)
Ta có bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020:
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
Chọn B.
Câu 7
Phương pháp:
Tiêu chí thống kê trong biểu đồ trên được biểu diễn trên trục thẳng đứng.
Cách giải:
Tiêu chí thống kê của biểu đồ trên là nhiệt độ.
Chọn D.
Câu 8
Phương pháp:
Chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – góc nhọn, từ đó suy ra cặp cạnh tương ứng bằng nhau.
Cách giải:
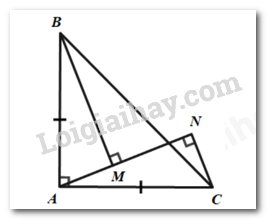
Vì \(\Delta ABC\) vuông tại \(A\) nên \(\angle BAC = \angle BAM + \angle CAM = 90^\circ \)
\( \Rightarrow \angle BAM = 90^\circ - \angle CAM\)
Và \(\Delta ANC\) vuông tại \(N\) nên \(\angle ACN + \angle CAM = 90^\circ \) (hai góc phụ nhau)
\( \Rightarrow \angle ACN = 90^\circ - \angle CAM\)
Do đó \(\angle BAM = \angle ACN\)
Xét \(\Delta BAM\) và \(\Delta ACN\) có:
\(\angle BMA = \angle ANC = 90^\circ \)
\(\angle BAM = \angle ACN\) (cmt)
\(AB = AC\) (gt)
Nên \(\Delta BAM = \Delta ACN\) (cạnh huyền – góc nhọn).
Suy ra: \(MA = NC\) (hai cạnh tương ứng) nên A đúng
\(BM = AN\) (hai cạnh tương ứng) nên B đúng
\(\angle ABM = \angle CAN\) (hai góc tương ứng) nên D đúng
Chọn C.
Câu 9
Phương pháp:
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Cách giải:
Từ các hình vẽ, ta nhận thấy Hình 3 là hình vẽ của hai góc đối đỉnh.
Chọn C.
Câu 10
Phương pháp:
Vận dụng tính chất của hai đường thẳng song song: Hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hai góc đối đỉnh thì bằng nhau.
Cách giải:
Vì \(yy'//zz'\) nên \(\angle xAy' = \angle xBz' = {60^0}\) (hai góc đồng vị)
Vì \(\angle xBz'\) và \(\angle zBx'\) là hai đối đỉnh nên \(\angle xBz' = \angle zBx' = {60^0}\).
Vậy \(\angle zBx' = {60^0}\)
Chọn D.
Phần II. Tự luận (7 điểm):
Bài 1
Phương pháp:
a) Đổi hỗn số sang phân số.
Thực hiện các phép toán với số hữu tỉ.
b) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\)
Lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
Tính \({\left( {a.b} \right)^m} = {a^m}.{b^m}\)
c) Tính căn bậc hai số học của một số thực
Thực hiện các phép toán với số hữu tỉ.
d) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\left( {2\dfrac{5}{6} + 1\dfrac{4}{9}} \right):\left( {10\dfrac{1}{{12}} - 9,5} \right)\)
\(\begin{array}{l} = \left( {\dfrac{{17}}{6} + \dfrac{{13}}{9}} \right):\left( {\dfrac{{121}}{{12}} - \dfrac{{19}}{2}} \right)\\ = \left( {\dfrac{{51}}{{18}} + \dfrac{{26}}{{18}}} \right):\left( {\dfrac{{121}}{{12}} - \dfrac{{114}}{{12}}} \right)\\ = \dfrac{{77}}{{18}}:\dfrac{7}{{12}} = \dfrac{{77}}{{18}}.\dfrac{{12}}{7}\\ = \dfrac{{22}}{3}\end{array}\)
b) \(\dfrac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
\(\begin{array}{l} = \dfrac{{{{\left( {{2^5}} \right)}^3}.{{\left( {{3^2}} \right)}^5}}}{{{{\left( {{2^3}} \right)}^3}.{{\left( {2.3} \right)}^6}}} = \dfrac{{{2^{5.3}}{{.3}^{2.5}}}}{{{2^{3.3}}{{.2}^6}{{.3}^6}}}\\ = \dfrac{{{2^{15}}{{.3}^{10}}}}{{{2^9}{{.2}^6}{{.3}^6}}} = \dfrac{{{2^{15}}{{.3}^{10}}}}{{{2^{9 + 6}}{{.3}^6}}}\\ = \dfrac{{{2^{15}}{{.3}^{10}}}}{{{2^{15}}{{.3}^6}}} = \dfrac{{{3^{10}}}}{{{3^6}}}\\ = {3^{10 - 6}} = {3^4} = 81\end{array}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\dfrac{{25}}{{16}}} \)
\(\begin{array}{l} = \sqrt {{8^2}} + 2.\sqrt {{3^2}} - 8.\sqrt {{{\left( {\dfrac{5}{4}} \right)}^2}} \\ = 8 + 2.3 - 8.\dfrac{5}{4}\\ = 8 + 6 - 10\\ = 4\end{array}\)
d) \(\left| {\dfrac{1}{{ - 5}}} \right| - \dfrac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \dfrac{{\left| 2 \right|}}{5}\)
\(\begin{array}{l} = \dfrac{1}{5} - \dfrac{4}{5} - \dfrac{2}{5}\\ = \dfrac{{ - 5}}{5} = - 1\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
b) Biến đổi về dạng \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
c) Tính căn bậc hai số học của số thực
Đổi hỗn số sang phân số
Thực hiện các phép toán với số hữu tỉ
Vận dụng quy tắc chuyển vế, tìm \(x\).
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(x - \dfrac{1}{2} = 3\dfrac{1}{2}:\dfrac{2}{7}\)
\(\begin{array}{l}x - \dfrac{1}{2} = \dfrac{7}{2}:\dfrac{2}{7}\\x - \dfrac{1}{2} = \dfrac{7}{2}.\dfrac{2}{7} = 1\\x = 1 + \dfrac{1}{2} = \dfrac{2}{2} + \dfrac{1}{2}\\x = \dfrac{3}{2}\end{array}\)
Vậy \(x = \dfrac{3}{2}\)
b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
\(\begin{array}{l}{3^{ - 1 + x}} + {5.3^{x - 1}} = 162\\{3^{x - 1}}.\left( {1 + 5} \right) = 162\\{3^{x - 1}}.6 = 162\\{3^{x - 1}} = 162:6\\{3^{x - 1}} = 27\\{3^{x - 1}} = {3^3}\\ \Rightarrow x - 1 = 3\\\,\,\,\,\,\,\,x = 3 + 1\end{array}\)
\(x = 4\) (thỏa mãn \(x\) là số nguyên)
Vậy \(x = 4\)
c) \(\sqrt {1,96} + 3\dfrac{x}{4} = \sqrt {0,04} + \dfrac{1}{4}.\sqrt {{{\left( {\dfrac{{89}}{5}} \right)}^2}} \)
\(\begin{array}{l}\sqrt {{{\left( {1,4} \right)}^2}} + \dfrac{{12 + x}}{4} = \sqrt {{{\left( {0,2} \right)}^2}} + \dfrac{1}{4}.\dfrac{{89}}{5}\\1,4 + \dfrac{{12 + x}}{4} = 0,2 + \dfrac{{89}}{{20}}\\\dfrac{{12 + x}}{4} = 0,2 + \dfrac{{89}}{{20}} - 1,4\\\dfrac{{12 + x}}{4} = \dfrac{4}{{20}} + \dfrac{{89}}{{20}} - \dfrac{{28}}{{20}}\\\dfrac{{12 + x}}{4} = \dfrac{{13}}{4}\\ \Rightarrow 12 + x = 13\\\,\,\,\,\,\,\,x = 13 - 12\\\,\,\,\,\,\,\,x = 1\end{array}\)
Vậy \(x = 1\)
d) \(\left| {2x:\dfrac{4}{5} - \dfrac{{1,6}}{4}} \right| = \dfrac{7}{5}\)
\(\left| {2x:\dfrac{4}{5} - \dfrac{2}{5}} \right| = \dfrac{7}{5}\)
|
Trường hợp 1: \(\begin{array}{l}2x:\dfrac{4}{5} - \dfrac{2}{5} = \dfrac{7}{5}\\2x:\dfrac{4}{5} = \dfrac{7}{5} + \dfrac{2}{5}\\2x:\dfrac{4}{5} = \dfrac{9}{5}\\2x = \dfrac{9}{5}.\dfrac{4}{5} = \dfrac{{36}}{{25}}\\x = \dfrac{{36}}{{25}}:2 = \dfrac{{36}}{{25}}.\dfrac{1}{2}\\x = \dfrac{{18}}{{25}}\end{array}\) Vậy \(x \in \left\{ {\dfrac{{18}}{{25}};\dfrac{{ - 2}}{5}} \right\}\) |
Trường hợp 2: \(\begin{array}{l}2x:\dfrac{4}{5} - \dfrac{2}{5} = \dfrac{{ - 7}}{5}\\2x:\dfrac{4}{5} = \dfrac{{ - 7}}{5} + \dfrac{2}{5}\\2x:\dfrac{4}{5} = \dfrac{{ - 5}}{5} = - 1\\2x = - 1.\dfrac{4}{5} = \dfrac{{ - 4}}{5}\\x = \dfrac{{ - 4}}{5}:2 = \dfrac{{ - 4}}{5}.\dfrac{1}{2}\\x = \dfrac{{ - 2}}{5}\end{array}\)
|
Bài 3
Phương pháp:
a) Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
b) + Hai góc kề bù có tổng bằng \(180^\circ \)
+1 góc bằng \(90^\circ \) thì hai đường thẳng vuông góc với nhau.
c) + Hai tam giác bằng nhau có các cặp cạnh, cặp góc tương ứng bằng nhau
+ Hai đường thẳng song song có các cặp góc so le trong bằng nhau.
Cách giải:
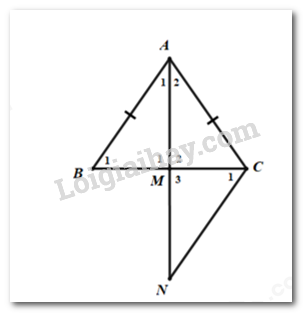
a) Xét tam giác \(ABM\) và tam giác \(ACM\), ta có:
\(AB = AC\) (giả thiết)
\(BM = MC\)(\(M\) là trung điểm của \(BC\))
\(AM\) là cạnh chung
Suy ra \(\Delta ABM = \Delta ACM\) (c.c.c)
\( \Rightarrow \angle {A_1} = \angle {A_2}\) (hai góc tương ứng) hay \(AM\) là tia phân giác của \(\angle BAC\)
\( \Rightarrow \angle {M_1} = {M_2}\) (hai góc tương ứng).
b) Mà \(\angle {M_1} + \angle {M_2} = 180^\circ \) (kề bù) nên \(\angle {M_1} = \angle {M_2} = 90^\circ \).
Suy ra \(AM \bot BC\).
c) \({\rm{Ta}}\) có \(CN{\rm{ // }}AB\) nên \(\angle {B_1} = \angle {C_1}\) (hai góc so le trong).
Xét \(\Delta ABM\) và \(NCM\), ta có:
\(\angle {M_1} = {M_2}\) (hai góc đối đỉnh)
\(MB = MC\) (\(M\) là trung điểm của \(BC\))
\(\angle {B_1} = \angle {C_1}\) (chứng minh trên)
Suy ra \(\Delta ABM = \Delta NCM\) (g.c.g) \( \Rightarrow AM = MN\) (hai cạnh tương ứng).
Suy ra \(M\) là trung điểm của \(AN\).
Bài 4
Phương pháp:
Để \(P = \dfrac{{M\left( x \right)}}{{n\left( x \right)}}\) có giá trị nguyên
+ Bước 1: Biến đổi \(P = m\left( x \right) + \dfrac{k}{{n\left( x \right)}}\). Trong đó \(k\) là số nguyên
+ Bước 2: Lập luận: Để \(P\) có giá trị nguyên thì \(k \vdots n\left( x \right)\) hay \(n\left( x \right) \in U\left( k \right)\)
+ Bước 3: Lập bảng giá trị và kiểm tra \(x\) với điều kiện đã tìm
+ Bước 4: Kết luận
Cách giải:
\(G = \dfrac{{\sqrt x + 5}}{{\sqrt x - 3}}\) (điều kiện: \(x \ge 0\))
\(\begin{array}{l} = \dfrac{{\sqrt x - 3 + 8}}{{\sqrt x - 3}}\\ = \dfrac{{\sqrt x - 3}}{{\sqrt x - 3}} + \dfrac{8}{{\sqrt x - 3}}\\ = 1 + \dfrac{8}{{\sqrt x - 3}}\end{array}\)
Để \(G \in \mathbb{Z}\) thì \(\dfrac{8}{{\sqrt x - 3}} \in \mathbb{Z}\)
Vì \(x \in \mathbb{Z}\) suy ra \(\sqrt x \in \mathbb{Z}\) (\(x\) là số chính phương) hoặc \(\sqrt x \in I\) (là số vô tỉ)
TH1: \(\sqrt x \in I\) là số vô tỉ \( \Rightarrow \sqrt x - 3\) là số vô tỉ
\( \Rightarrow \dfrac{8}{{\sqrt x - 3}}\) là số vô tỉ (Loại)
TH2: \(\sqrt x \in \mathbb{Z} \Rightarrow \sqrt x - 3 \in \mathbb{Z}\)
\(\dfrac{8}{{\sqrt x - 3}} \in \mathbb{Z} \Rightarrow 8 \vdots \left( {\sqrt x - 3} \right)\) hay \(\left( {\sqrt x - 3} \right) \in \)Ư\(\left( 8 \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\)
Ta có bảng sau:
|
\(\sqrt x - 3\) |
\( - 8\) |
\( - 4\) |
\( - 2\) |
\( - 1\) |
\(1\) |
\(2\) |
\(4\) |
\(8\) |
|
\(\sqrt x \) |
\( - 5\) |
\( - 1\) |
1 |
2 |
4 |
5 |
7 |
\(11\) |
|
\(x\) |
Loại (vì \(\sqrt x = - 5\)) |
Loại (vì\(\sqrt x = - 1\)) |
\(1\left( {tm} \right)\) |
\(4\left( {tm} \right)\) |
\(16\left( {tm} \right)\) |
\(25\left( {tm} \right)\) |
\(49\left( {tm} \right)\) |
\(121\left( {tm} \right)\) |
Vậy để \(G\)có giá trị nguyên thì \(x \in \left\{ {1;4;16;25;49;121} \right\}\)
- Đề thi học kì 1 Toán 7 - Đề số 7 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 8 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 9 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 10 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 11 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay












Danh sách bình luận