Đề thi giữa kì 1 Toán 7 - Đề số 7 - Kết nối tri thức

Đề bài

Phần trắc nghiệm (3 điểm)

Câu 1. Tập hợp số hữu tỉ \(\mathbb{Q}\) gồm:

A. Số hữu tỉ âm                               

B. Số hữu tỉ dương.                        

C. Số nguyên âm; số nguyên dương và số 0.      

D. Số hữu tỉ dương; số hữu tỉ âm và số 0.

Câu 2.  Số không phải số hữu tỉ là

A. \(\frac{{2022}}{0}\).

B. \(0,5\).

C. -2.

D. \(2\frac{1}{5}\).

Câu 3.  Chu kỳ của số thập phân vô hạn tuần hoàn\( - 5,21\left( 2 \right)\) là:

A. \(212\).

B. \(2\).

C. \(12\).

D. \(0,212\).

Câu 4.  Giá trị của biểu thức \({3^6}.\frac{1}{{81}}\) là

A. \(1\).

B. \(9\).

C. \({9^2}\).

D. \({9^4}\).

Câu 5. ­ Căn bậc hai số học của 16 là

A. 4.

B. -4.

C. \( \pm 4\).

D. 8

Câu 6. ­ Số \(\sqrt 5 \) thuộc tập hợp số:

A. \(\mathbb{R}\).

B. \(\mathbb{Z}\).

C. \(\mathbb{Q}\).

D. \(\mathbb{N}\).

Câu 7.  \(\left| { - 1,5} \right|\) bằng

A. \(2\).

B. \( - 1,5\).

C. \(1,5\).

D. \( - 2\).

Câu 8.  Khẳng định đúng là:

A. Hai góc đối đỉnh thì bù nhau.    

B. Hai góc đối đỉnh thì bằng nhau.

C. Hai góc bằng nhau thì đối đỉnh.

D. Hai góc đối đỉnh thì phụ nhau.

Câu 9. Trong hình vẽ dưới, các tia phân giác là.

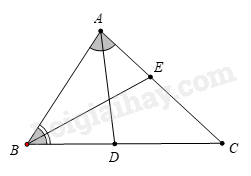
A. \(AB,BE\).

B. \(AD,BC\).

C. \(AD,BE\).

D. \(AD,AB\).

Câu 10.  Qua một điểm ở ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?

A. Không có.

B. Có vô số.

C. Có ít nhất một.

D. Chỉ có một.

Câu 11.  Chọn câu trả lời đúng.

Trong định lí: " Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia. "

Ta có giả thiết là:

A. "Nếu một đường thẳng vuông góc".

B. "Nó cũng vuông góc với đường thẳng kia".

C. "Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia".

D. "Một đường thẳng vuông góc với một trong hai đường thẳng song song".

Câu 12.  Cho hình vẽ, biết \(x\,{\rm{//}}\,y\) và \(\widehat {{{M}_1}}{ = }55^\circ \). Tính số đo góc \({N_1}\).

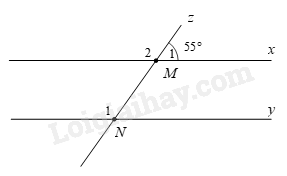
A. \(\widehat {{{N}_1}}{ = }35{^\circ }\).

B. \(\widehat {{{N}_1}}{ = }55{^\circ }\).

C. \(\widehat {{{N}_1}}{ = }65{^\circ }\).

D. \(\widehat {{{N}_1}}{ = }125{^\circ }\).

PHẦN TỰ LUẬN (7,0 điểm)

Câu 13 (2 điểm) Thực hiện phép tính

a) \(\frac{{ - 4}}{{12}} + \frac{{14}}{{21}}\)

b) \(\frac{{ - 8}}{3}.\frac{2}{{11}} - \frac{8}{3}:\frac{{11}}{9}\)

c) \(0,1.\sqrt 4 + 2.\sqrt {16} \)

d) \(\frac{3}{2}{.2^2} + \frac{5}{2}.\left( { - 4} \right) + {2022^0}\)

Câu 14 (1 điểm) Tìm \(x\), biết:

a) \(\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4\)

b) \(\left| {x - 1} \right| = 4\)

Câu 15 (1 điểm)  Cho hình vẽ sau, hãy chỉ ra:

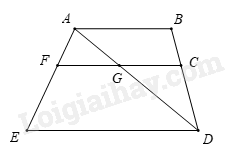
a) Các cặp góc kề bù.

b) Các cặp góc đối đỉnh.

Câu 16 (2 điểm) Cho \(\Delta ABC\) có \(\widehat {ABC} = 70^\circ ,\,\,\widehat {ACB} = 40^\circ \). Vẽ tia \(Cx\) là tia đối của tia \(CB\). Vẽ tia \(Cy\) là tia phân giác của \(\widehat {ACx}\).

a) Tính \(\widehat {ACx},\,\,\widehat {xCy}\).                 

b) Chứng minh rằng \(AB\,{\rm{//}}\,Cy\).

Câu 17 (1 điểm) Theo yêu cầu của bác An, diện tích phòng ngủ tối thiểu đạt 25m². Trên bản vẽ có tỉ lệ \(\frac{1}{{100}}\), kích thước phòng ngủ trên bản vẽ tính bằng centimet. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của bác An không? Vì sao?

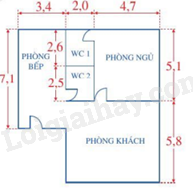
-------- Hết --------

Lời giải

Phần trắc nghiệm (3 điểm)

Câu 1. Tập hợp số hữu tỉ \(\mathbb{Q}\) gồm:

A. Số hữu tỉ âm                               

B. Số hữu tỉ dương.                        

C. Số nguyên âm; số nguyên dương và số 0.                       

D. Số hữu tỉ dương; số hữu tỉ âm và số 0.

Phương pháp

Dựa vào khái niệm tập hợp số hữu tỉ.

Lời giải

Tập hợp số hữu tỉ \(\mathbb{Q}\) gồm số hữu tỉ dương, số hữu tỉ âm và số 0.

Đáp án D.

Câu 2.  Số không phải số hữu tỉ là

Phương pháp

Dựa vào khái niệm số hữu tỉ.

Lời giải

\(\frac{{2022}}{0}\) không phải số hữu tỉ vì mẫu số bằng 0.

Đáp án A.

Câu 3.  Chu kỳ của số thập phân vô hạn tuần hoàn \( - 5,21\left( 2 \right)\) là:

Phương pháp

Dựa vào khái niệm số thập phân vô hạn tuần hoàn.

Lời giải

Chu kỳ của số thập phân vô hạn tuần hoàn \( - 5,21\left( 2 \right)\) là 2.

Đáp án B.

Câu 4.  Giá trị của biểu thức \({3^6}.\frac{1}{{81}}\) là

Phương pháp

Phân tích 81 thành lũy thừa với số mũ tự nhiên của 3 để rút gọn biểu thức.

Lời giải

\({3^6}.\frac{1}{{81}} = \frac{{{3^6}}}{{{3^4}}} = {3^{6 - 4}} = {3^2} = 9\).

Đáp án B.

Câu 5. ­ Căn bậc hai số học của 16 là

Phương pháp

Dựa vào kiến thức về căn bậc hai số học.

Lời giải

Căn bậc hai số học của 16 là 4.

Đáp án A.

Câu 6. ­ Số \(\sqrt 5 \) thuộc tập hợp số:

Phương pháp

Dựa vào đặc điểm của các tập hợp số đã học.

Lời giải

\(\sqrt 5 \) là số vô tỉ nên \(\sqrt 5 \) thuộc tập hợp \(\mathbb{R}\).

Đáp án A.

Câu 7. \(\left| { - 1,5} \right|\) bằng

Phương pháp

Dựa vào kiến thức về giá trị tuyệt đối.

Lời giải

Vì -1,5 < 0 \(\left| { - 1,5} \right|\) = - (-1,5) = 1,5.

Đáp án C.

Câu 8.  Khẳng định đúng là:

A. Hai góc đối đỉnh thì bù nhau.    

B. Hai góc đối đỉnh thì bằng nhau.

C. Hai góc bằng nhau thì đối đỉnh.

D. Hai góc đối đỉnh thì phụ nhau.

Phương pháp

Dựa vào tính chất của hai góc đối đỉnh.

Lời giải

Hai góc đối đỉnh thì bằng nhau.

Đáp án B.

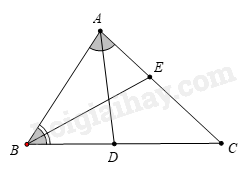
Câu 9. Trong hình vẽ dưới, các tia phân giác là.

Phương pháp

Quan sát hình để tìm các tia phân giác.

Lời giải

Quan sát hình vẽ ta thấy AD là tia phân giác của \(\widehat {BAC}\); BE là tia phân giác của \(\widehat {ABC}\).

Đáp án C.

Câu 10.  Qua một điểm ở ngoài một đường thẳng, có bao nhiêu đường thẳng song song với đường thẳng đó?

Phương pháp

Dựa vào kiến thức về hai đường thẳng song song.

Lời giải

Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.

Đáp án D.

Câu 11.  Chọn câu trả lời đúng.

Trong định lí: " Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia. "

Ta có giả thiết là:

A. "Nếu một đường thẳng vuông góc".

B. "Nó cũng vuông góc với đường thẳng kia".

C. "Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia".

D. "Một đường thẳng vuông góc với một trong hai đường thẳng song song".

Phương pháp

Dựa vào khái niệm giả thiết và kết luận.

Lời giải

Giả thiết của định lý là điều cho biết: “một đường thẳng vuông góc với một trong hai đường thẳng song song”

Đáp án D.

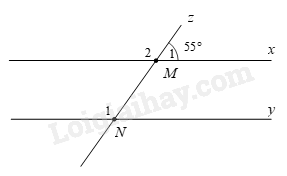
Câu 12.  Cho hình vẽ, biết \(x\,{\rm{//}}\,y\) và \(\widehat {{{M}_1}}{ = }55^\circ \). Tính số đo góc \({N_1}\).

Phương pháp

x // y nên ta có các cặp góc bằng nhau, xác định số đo góc N₁.

Lời giải

Ta có \(\widehat {{M_1}}\) và \(\widehat {{M_2}}\) là hai góc kề bù nên \(\widehat {{M_1}} + \widehat {{M_2}} = {180^0}\).

\(\widehat {{M_1}} = {55^o} \Rightarrow \widehat {{M_2}} = {180^0} - \widehat {{M_1}} = {180^0} - {55^0} = {125^0}\)

Vì x // y nên \(\widehat {{N_1}} = \widehat {{M_1}}\) (hai góc đồng vị).

Vậy \(\widehat {{{N}_1}}{ = }125{^\circ }\).

Đáp án D.

Phần tự luận.

Câu 13 (2 điểm) Thực hiện phép tính

Phương pháp

Sử dụng quy tắc tính để giải bài tập.

Lời giải

a) \(\frac{{ - 4}}{{12}} + \frac{{14}}{{21}} = \frac{{ - 1}}{3} + \frac{2}{3} = \frac{1}{3}\)

b) \(\frac{{ - 8}}{3}.\frac{2}{{11}} - \frac{8}{3}:\frac{{11}}{9} = \frac{{ - 8}}{3}.\frac{2}{{11}} + \left( {\frac{{ - 8}}{3}} \right).\frac{9}{{11}} = \frac{{ - 8}}{3}.\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right)\)\( = \frac{{ - 8}}{3}.1 = \frac{{ - 8}}{3}\)

c) \(0,1.\sqrt 4  + 2.\sqrt {16}  = 0,1.2 + 2.4\)\( = 0,2 + 8 = 8,2\)

d) \(\frac{3}{2}{.2^2} + \frac{5}{2}.\left( { - 4} \right) + {2022^0} = 6 - 10 + 1\)\( =  - 3\)

Câu 14 (1 điểm) Tìm \(x\), biết:

Phương pháp

Dựa vào quy tắc tính để tìm x.

Lời giải

a) \(\left( {x - \frac{3}{5}} \right):\frac{{ - 1}}{3} = 0,4\)

\(\left( {x - \frac{3}{5}} \right) = \frac{2}{5}.\frac{{ - 1}}{3}\)

\(x - \frac{3}{5} = \frac{{ - 2}}{{15}}\)

\(x = \frac{{ - 2}}{{15}} + \frac{3}{5}\)

\(x = \frac{7}{{15}}\)

Vậy \(x = \frac{7}{{15}}\).

b) \(\left| {x - 1} \right| = 4\)

\( \Rightarrow x - 1 = 4\) hoặc \(x - 1 =  - 4\)

\( \Rightarrow x = 5\) hoặc \(x =  - 3\)

Vậy \(x = 5\) hoặc \(x =  - 3\)

Câu 15 (1 điểm)  Cho hình vẽ sau, hãy chỉ ra:

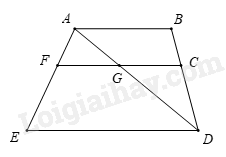
a) Các cặp góc kề bù.

b) Các cặp góc đối đỉnh.

Phương pháp

Dựa vào khái niệm hai góc kề bù, hai góc đối đỉnh.

Lời giải

a) Các cặp góc kề bù là: \(\widehat {FGA}\) và \(\widehat {AGC}\); \(\widehat {AGC}\) và \(\widehat {CGD}\); \(\widehat {CGD}\) và \(\widehat {DGF}\); \(\widehat {DGF}\) và \(\widehat {FGA}\).

b) Các cặp góc đối đỉnh là: \(\widehat {FGA}\) và \(\widehat {CGD}\); \(\widehat {DGF}\) và \(\widehat {AGC}\).

Câu 16 (2 điểm) Cho \(\Delta ABC\) có \(\widehat {ABC} = 70^\circ ,\,\,\widehat {ACB} = 40^\circ \). Vẽ tia \(Cx\) là tia đối của tia \(CB\). Vẽ tia \(Cy\) là tia phân giác của \(\widehat {ACx}\).

a) Tính \(\widehat {ACx},\,\,\widehat {xCy}\).                 

b) Chứng minh rằng \(AB\,{\rm{//}}\,Cy\).

Phương pháp

a) Dựa vào tính chất của hai góc kề bù và tính chất của tia phân giác để tính \(\widehat {ACx},\,\,\widehat {xCy}\).

b) Chứng minh AB và Cy có hai góc đồng vị bằng nhau nên song song.

Lời giải

a) Ta có: \(\widehat {ACx} + \widehat {ACB} = 180^\circ \) (hai góc kề bù) nên \(\widehat {ACx} = 180^\circ  - \widehat {ACB} = 180^\circ  - 40^\circ  = 140^\circ \).

Vì \(Cy\) là tia phân giác của \(\widehat {ACx}\) nên \(\widehat {xCy} = \widehat {ACy} = \frac{{\widehat {ACx}}}{2} = \frac{{140^\circ }}{2} = 70^\circ \).

b) Ta có: \(\widehat {ABC} = \widehat {xCy} = 70^\circ \). Mà hai góc ở vị trí đồng vị nên \(AB\,{\rm{//}}\,Cy\).

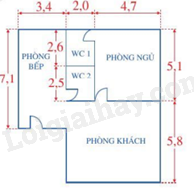
Câu 17 (1 điểm) Theo yêu cầu của bác An, diện tích phòng ngủ tối thiểu đạt 25m². Trên bản vẽ có tỉ lệ \(\frac{1}{{100}}\), kích thước phòng ngủ trên bản vẽ tính bằng centimet. Khoảng cách trên bản vẽ như vậy có phù hợp với yêu cầu của bác An không? Vì sao?

Phương pháp

Tính kích thước phòng ngủ thực tế theo bản vẽ.

Tính diện tích phòng ngủ thực tế theo bản vẽ.

Kiểm tra xem kết quả có phù hợp với yêu cầu của bác An không.

Lời giải

Kích thước phòng ngủ thực tế theo bản vẽ là:

\(4,7:\frac{1}{{100}}\; = 4,7.{\rm{ }}100 = {\rm{ }}4700cm = {\rm{ }}4,7m\)

\(5,1:\frac{1}{{100}} = 5,1.{\rm{ }}100 = 5100cm{\rm{ }} = {\rm{ }}5,1m\)

Diện tích phòng ngủ thực tế theo bản vẽ:

4,7. 5,1= 23,97 m²

Theo yêu cầu của bác An, diện tích phòng ngủ tối thiểu đạt 25 m² mà thực tế theo bản vẽ, diện tích phòng ngủ là 23,97 m² < 25 m². Như vậy kích thước phòng ngủ như trong bản vẽ không phù hợp với yêu cầu của bác An.