 Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi học kì 1 Toán 7 Kết nối tri thức
Đề thi học kì 1 Toán 7 Kết nối tri thức Đề thi học kì 1 Toán 7 - Đề số 10 - Kết nối tri thức
Tải vềI. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các câu sau câu nào đúng?
A. \(\dfrac{3}{7} \in \mathbb{Q}\)
B. \(\dfrac{1}{2} \in \mathbb{Z}\)
C. \(\dfrac{{ - 9}}{5} \notin \mathbb{Q}\)
D. \( - 6 \in \mathbb{N}\)
Câu 2: Tập hợp các số hữu tỉ kí hiệu là:
A. N
B. \({N^*}\)
C. Q
D. Z
Câu 3: Số đối cùa \(\dfrac{{ - 2}}{3}\) là:
A. \(\dfrac{2}{3}\)
B. \(\dfrac{3}{2}\)
C. \(\dfrac{{ - 3}}{2}\)
D. \(\dfrac{2}{{ - 3}}\)
Câu 4: Điểm B trên trục số biểu diễn số hữu tỉ nào sau đây?
A. \(\dfrac{{ - 2}}{3}\)
B. \(\dfrac{{ - 2}}{5}\)
C. \( - \dfrac{1}{3}\)
D. \(\dfrac{2}{6}\)
Câu 5: Phép tính nào sau đây không đúng?
A. \({x^{18}}:{x^6} = {x^{12}}\left( {x \ne 0} \right)\)
B. \({x^4}.{x^8} = {x^{12}}\)
C. \({x^2}.{x^6} = {x^{12}}\)
D. \({({x^3})^4} = {x^{12}}\)
Câu 6: Cho các số sau \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3;\dfrac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn?
A. \(\dfrac{4}{6} = 0,66...6;\dfrac{{20}}{{15}} = 1,333....3\)
B. \(\dfrac{3}{4} = 0,75;\dfrac{5}{4} = 1,25\)
C. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75\)
D. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3\)
Câu 7: Cho tam giác \(ABC\) cân tại \(A\). Phát biểu nào trong các phát biểu sau là sai?
A. \(\angle B = \angle C\)
B. \(\angle C = \dfrac{{180^\circ - \angle A}}{2}\)
C. \(\angle A = 180^\circ - 2\angle C\)
D. \(\angle B \ne \angle C\)
Câu 8: Chọn câu trả lời sai:
Biểu đồ đoạn thẳng biểu diễn sự thay đổi của một đối tượng theo thời gian thì:
A. Trục đứng biểu diễn đại lượng ta đang quan tâm
B. Trục ngang biểu diễn thời gian;
C. Trục đứng biểu diễn các tiêu chí thống kê
D. Các đoạn thẳng nối nhau tạo thành một đường gấp khúc.
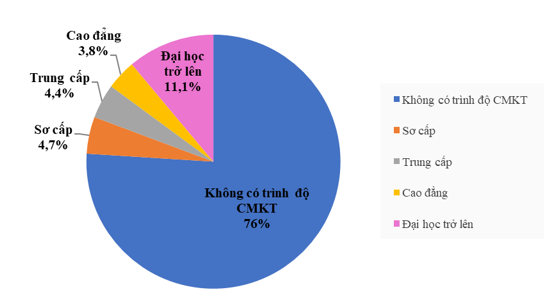
Câu 9: Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) lực lượng lao động (từ 15 tuổi trở lên) phân theo trình độ chuyên môn kĩ thuật (CMKT) của nước ta (năm 2020).
Trong năm 2020, lực lượng lao động không có trình độ CMKT gấp bao nhiêu lần lực lượng lao động có trình độ đại học trở lên (làm tròn đến hàng phần mười)?
A. 6,7
B. 6,8
C. 6,9
D. 7
Câu 10: Tiên đề Euclid được phát biểu: “Qua một điểm M nằm ngoài đường thẳng a...”.
A. Có duy nhất một đường thẳng đi qua M và song song với a.
B. Có hai đường thẳng song song với a.
C. Có ít nhất một đường thẳng song song với a.
D. Có vô số đường thẳng song song với a.
Câu 11: Nếu \(\Delta ABC = \Delta DEF\) và \(\angle B = {70^0};\angle F = {40^0}\) thì góc \(A\) bằng:
A. \({110^0}\)
B. \({70^0}\)
C. \({30^0}\)
D. \({40^0}\)
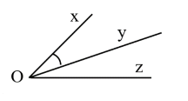
Câu 12: Cho hình vẽ, biết\(\widehat {\;xOy} = {20^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz\;}\)bằng:
A. \({20^0}\)
B. \(\;{160^0}\)
C. \({80^0}\)
D. \(\;{40^0}\)
II. TỰ LUẬN (7 điểm)
Câu 1: (2 điểm) Tính:
a) \(\sqrt 9 - \dfrac{2}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0}\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3}\)
Câu 2: (1,5 điểm) Tìm x:
a) \(2x - 3,7 = 10\)
b) \(\sqrt {49} + 5x - 1 = {\left( { - 2} \right)^3}\)
c) \(\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}\)
Câu 3: (3,0 điểm)
Cho tam giác \(ABC\) vuông tại \(A,M\) là trung điểm của \(AC\). Trên tia đối của tia \(MB\) lấy điểm \(K\) sao cho \(BM = MK.\)
a) Chứng minh: \(\Delta ABM = \Delta CKM\);
b) Chứng minh: \(BC = AK\);
c) Chứng minh: \(CK \bot AC\).
Câu 4: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức \(M = \sqrt {{x^2} + 169} - 2024\).
Lời giải
I. Phần trắc nghiệm (3 điểm)
|
Câu |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Đáp án |
A |
C |
A |
C |
C |
B |
D |
C |
B |
A |
B |
A |
Câu 1
Phương pháp:
Tập hợp các số tự nhiên: N = {0;1;2;3;…}
Tập hợp các số nguyên: Z = {-3;-2;-1;0;1;2;3;….}
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
\(\dfrac{3}{7} \in \mathbb{Q}\) nên A đúng.
\(\dfrac{1}{2} \notin \mathbb{Z}\) nên B sai
\(\dfrac{{ - 9}}{5} \in \mathbb{Q}\) nên C sai
\( - 6 \notin \mathbb{N}\) nên D sai.
Chọn A.
Câu 2
Phương pháp:
Tập hợp các số hữu tỉ \(Q = \left\{ {\dfrac{a}{b}|a,b \in Z,b \ne 0} \right\}\)
Cách giải:
Tập hợp các số hữu tỉ kí hiệu là Q
Chọn C.
Câu 3
Phương pháp:
Hai số đối nhau nếu chúng có tổng là 0.
Số đối của số a là số -a.
Cách giải:
Số đối của \(\dfrac{{ - 2}}{3}\) là \(\dfrac{2}{3}\)
Chọn A.
Câu 4
Phương pháp:
Xác định 1 đơn vị được chia thành bao nhiêu phần.
Các số nằm bên trái gốc O là các số âm.
Cách giải:
Điểm B nằm bên trái gốc O và cách gốc O một khoảng bằng \(\dfrac{1}{3}\) nên điểm B biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{3}\).
Chọn C.
Câu 5
Phương pháp:
Các phép tính với lũy thừa
Cách giải:
\({x^{18}}:{x^6} = {x^{18 - 6}} = {x^{12}}\left( {x \ne 0} \right)\) nên A đúng
\({x^4}.{x^8} = {x^{4 + 8}} = {x^{12}}\) nên B đúng
\({x^2}.{x^6} = {x^{2 + 6}} = {x^8}\) nên C sai.
\({({x^3})^4} = {x^{3.4}} = {x^{12}}\) nên D đúng.
Chọn C.
Câu 6
Phương pháp:
Nhận biết số thập phân hữu hạn
Cách giải:
\(\dfrac{4}{6} = 0,66...6\) là số thập phân vô hạn tuần hoàn với chu kì 6.
\(\dfrac{3}{4} = 0,75\) là số thập phân hữu hạn.
\(\dfrac{{20}}{{15}} = 1,333....3\) là số thập phân vô hạn tuần hoàn với chu kì 3.
\(\dfrac{5}{4} = 1,25\) là số thập phân hữu hạn
Vậy các số thập phân hữu hạn là \(\dfrac{3}{4} = 0,75\) và \(\dfrac{5}{4} = 1,25\)
Chọn B.
Câu 7
Phương pháp:
+ Tam giác cân có hai góc kề cạnh đáy bằng nhau
+ Tổng ba góc một tam giác bằng \(180^\circ \)
Cách giải:
Do tam giác \(ABC\)cân tại \(A\) nên \(\angle B = \angle C\) nên A đúng
Xét tam giác \(ABC\) ta có : \(\angle A + \angle B + \angle C = 180^\circ \)\( \Rightarrow \angle B + \angle C = 180^\circ - \angle A\)
\( \Rightarrow \angle B = \angle C = \dfrac{{180^\circ - \angle A}}{2}\) nên B đúng
hay \(\angle A = 180^\circ - 2\angle C\) nên C đúng
Chọn D.
Câu 8
Phương pháp:
Biểu đồ đoạn thẳng có trục nằm ngang biểu diễn thời gian, trục đứng biểu diễn đại lượng ta đang quan tâm
Các đoạn thẳng nối nhau tạo thành một đường gấp khúc cho ta thấy được sự thay đổi của dữ liệu theo các mốc thời gian
Cách giải:
Biểu đồ đoạn thẳng có trục nằm ngang biểu diễn thời gian, trục đứng biểu diễn đại lượng ta đang quan tâm. Các đoạn thẳng nối nhau tạo thành một đường gấp khúc nên C sai.
Chọn C.
Câu 9
Phương pháp:
Thực hiện phép chia 2 tỉ lệ
Cách giải:
Từ biểu đồ hình quạt tròn, ta thấy 76% lực lượng lao động không có trình độ CMKT; 11,1% lực lượng lao động có trình độ đại học trở lên.
Ta có: \(76\% :11,1\% = \dfrac{{76}}{{100}}:\dfrac{{11,1}}{{100}} = \dfrac{{76}}{{100}}.\dfrac{{100}}{{11,1}} = \dfrac{{76}}{{11,1}} = 6,\left( {846} \right) \approx 6,8\)
Vậy lực lượng lao động không có trình độ CMKT gấp 6,8 lần lực lượng lao động có trình độ đại học trở lên.
Chọn B.
Câu 10
Phương pháp:
Tiên đề Euclid.
Cách giải:
Qua một điểm M nằm ngoài đường thẳng a, có duy nhất một đường thẳng đi qua M và song song với a.
Chọn A.
Câu 11
Phương pháp:
Áp dụng tính chất hai tam giác bằng nhau
Áp dụng định lý tổng ba góc trong một tam giác.
Cách giải:
Theo giả thiết: \(\Delta ABC = \Delta DEF \Rightarrow \angle C = \angle F = {40^0}\) (hai góc tương ứng)
Tam giác \(ABC\) có: \(\angle A + \angle B + \angle C = {180^0}\)
\(\begin{array}{l} \Rightarrow \angle A = {180^0} - \left( {\angle B + \angle C} \right)\\ \Rightarrow \angle A = {180^0} - \left( {{{70}^0} + {{40}^0}} \right) = {70^0}\end{array}\)
Chọn B.
Câu 12
Phương pháp:
Nếu Om là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOm} = \widehat {yOm} = \dfrac{1}{2}.\widehat {xOy}\)
Cách giải:
Vì Oy là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {xOy} = \widehat {yOz} = {20^^\circ }\)
Chọn A.
II. Phần tự luận (7 điểm)
Câu 1
Phương pháp:
Thực hiện phép tính theo thứ tự thực hiện phép tính.
Tính căn bậc hai số học của một số.
Cách giải:
a) \(\sqrt 9 - \dfrac{2}{3} = 3 - \dfrac{2}{3} = \dfrac{9}{3} - \dfrac{2}{3} = \dfrac{7}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0} = - 5 + 5 + 1 = 1\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2 = {\left[ {{{\left( {\dfrac{1}{2}} \right)}^2}} \right]^2}.{\left( {\dfrac{1}{2}} \right)^5}.\dfrac{1}{2} = {\left( {\dfrac{1}{2}} \right)^4}.{\left( {\dfrac{1}{2}} \right)^5}.{\left( {\dfrac{1}{2}} \right)^1} = {\left( {\dfrac{1}{2}} \right)^{4 + 5 + 1}} = {\left( {\dfrac{1}{2}} \right)^{10}}\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3} = \dfrac{{25}}{{10}} + \dfrac{2}{3} - \dfrac{{10}}{3} = \dfrac{5}{2} - \dfrac{8}{3} = \dfrac{{15}}{6} - \dfrac{{16}}{6} = \dfrac{{ - 1}}{6}\)
Câu 2
Phương pháp:
\(\left| x \right| = a{\mkern 1mu} \) với \((a > 0)\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = a}\\{x = - a}\end{array}} \right.\)
Cách giải:
a)
\(\begin{array}{*{20}{l}}{2x - 3,7 = 10}\\{2x = 10 + 3,7}\\{2x = 13,7}\\{x = 13,7:2}\\{x = 6,85.}\end{array}\)
Vậy x = 6,85.
b)
\(\begin{array}{*{20}{l}}{\sqrt {49} + 5x - 1 = {{\left( { - 2} \right)}^3}}\\{7 + 5x - 1 = - 8}\\{5x = - 8 - 7 + 1}\\{5x = - 14}\\{x = \dfrac{{ - 14}}{5}}\end{array}\)
Vậy \(x = \dfrac{{ - 14}}{5}\)
c)
\(\begin{array}{*{20}{l}}{\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}}\\{ \Leftrightarrow \dfrac{8}{3}.|2x + 1| = \dfrac{{10}}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}:\dfrac{8}{3}}\\{ \Leftrightarrow |2x + 1| = \dfrac{{10}}{3}.\dfrac{3}{8}}\\{ \Leftrightarrow |2x + 1| = \dfrac{5}{4}}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x + 1 = \dfrac{5}{4}}\\{2x + 1 = \dfrac{{ - 5}}{4}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \dfrac{1}{4}}\\{2x = \dfrac{{ - 3}}{2}}\end{array}} \right.}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{1}{8}}\\{x = \dfrac{{ - 3}}{4}}\end{array}} \right.}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{1}{8};\dfrac{{ - 3}}{4}} \right\}\)
Câu 3
Phương pháp:
a) Vận dụng định nghĩa của hai tam giác bằng nhau, chứng minh \(\Delta ABM = \Delta CKM\left( {c.g.c} \right)\)
b) Vận dụng định nghĩa của hai tam giác bằng nhau, chứng minh \(\Delta AMK = \Delta CMB\left( {c.g.c} \right) \Rightarrow AK = BC\)
c) Chứng minh \(\angle MCK = {90^0}\)\( \Rightarrow CK \bot AC\) (vì \(M \in AC\))
Cách giải:
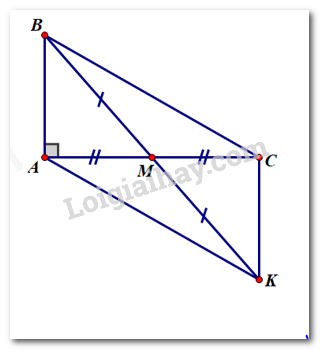
a) Vì \(M\) là trung điểm của \(AC \Rightarrow AM = MC\) (tính chất)
Có \(\angle AMB = \angle CMK\) (hai góc đối đính)
Xét \(\Delta ABM\) và \(\Delta CKM\) có:
\(\left. \begin{array}{l}AM = MC\left( {cmt} \right)\\\angle AMB = \angle CMK\left( {cmt} \right)\\BM = MK\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta ABM = \Delta CKM\left( {c.g.c} \right)\)
b) Có \(\angle AMK = \angle AMC\) (hai góc đối đỉnh)
Xét \(\Delta AMK\) và \(\Delta CMB\) có:
\(\left. \begin{array}{l}AM = MC\left( {cmt} \right)\\\angle AMK = \angle AMC\left( {cmt} \right)\\BM = MK\left( {gt} \right)\end{array} \right\} \Rightarrow \Delta AMK = \Delta CMB\left( {c.g.c} \right) \Rightarrow AK = BC\) (hai cạnh tương ứng)
c) Ta có: \(\Delta ABM = \Delta CKM \Rightarrow \angle BAM = \angle MCK\) (hai góc tương ứng)
Mà \(\angle BAM = {90^0}\) (do \(\Delta ABC\) vuông tại \(A\))
\( \Rightarrow \angle MCK = {90^0}\)
\( \Rightarrow CK \bot AM\)
\( \Rightarrow CK \bot AC\) (vì \(M \in AC\))
Câu 4
Phương pháp:
Dùng bất đẳng thức \({x^2} \ge 0,\forall x \in \mathbb{R}\).
Cách giải:
\(M = \sqrt {{x^2} + 169} - 2024\)
Vì \({x^2} \ge 0,\forall x \in \mathbb{R}\) nên \(M = \sqrt {{x^2} + 169} - 2024 \ge \sqrt {169} - 2024 = 13 - 2024 = - 2011.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0\).
Vậy min M = -2011 khi x = 0.
- Đề thi học kì 1 Toán 7 - Đề số 11 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 12 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 13 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 14 - Kết nối tri thức
- Đề thi học kì 1 Toán 7 - Đề số 15 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay













Danh sách bình luận