Bài 8 trang 159 SGK Đại số 10
Nêu cách giải hệ hai phương trình bậc nhất hai ẩn và giải hệ:
Đề bài
Nêu cách giải hệ hai bất phương trình bậc nhất hai ẩn và giải hệ: \(\left\{ \matrix{2x + y \ge 1 \hfill \cr x - 3y \le 1 \hfill \cr} \right.\)
Video hướng dẫn giải
Lời giải chi tiết
Cách giải hệ bất phương trình bậc nhất hai ẩn:
- Biểu diễn hình học miền nghiệm của từng bất phương trình trong hệ.
- Tìm miền giao của các tập nghiệm trên hình vẽ.
Áp dụng:
+ Ta dựng đường thẳng \((d): 2x + y = 1\) (tức là vẽ đồ thị hàm số \(y = -2x + 1\)).
Điểm \((0; 0) ∉ (d)\) ta có: \(2.0 + 0 < 1\) nên \(O\) không thuộc miền nghiệm.
Vậy nửa mặt phẳng bờ là \((d)\) không chứa điểm \((0; 0)\) là miền nghiệm của bất phương trình \(2x + y≥1\).
+ Ta dựng đường thẳng \(\Delta: x-3y-1=0 \Leftrightarrow y = \dfrac{1}{3}x - \dfrac{1}{3}\).
Điểm \(O(0;0)\) ta có: \(0-3.0\le 1\) nên điểm \(O\) thuộc miền nghiệm của bất phương trình \(x - 3y \le 1\).
Vậy nửa mặt phẳng bờ là đường thẳng \(\Delta \) có chứa điểm \(O\) là miền nghiệm của bpt \(x - 3y \le 1\).
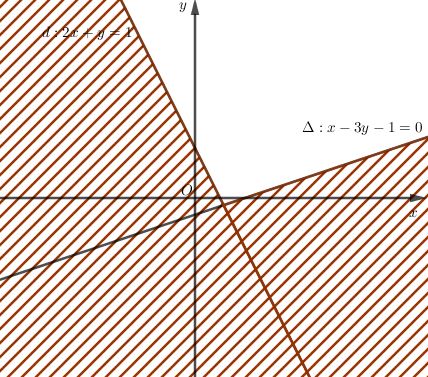
Dựng hình:
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1 trang 159 (Bài tập) SGK Đại số 10
- Bài 2 trang 160 SGK Đại số 10
- Bài 3 trang 160 SGK Đại số 10
- Bài 4 trang 160 SGK Đại số 10
- Bài 5 trang 160 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
