Bài 2 trang 159 SGK Đại số 10
Lập bảng biến thiên và vẽ đồ thị các hàm số.
Video hướng dẫn giải
Lập bảng biến thiên và vẽ đồ thị các hàm số.
LG a
\(y = -3x+2\)
Lời giải chi tiết:
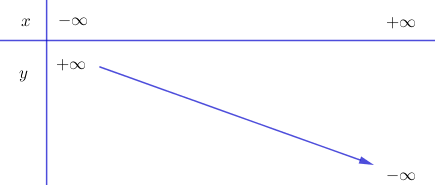
Ta có: a=-3 < 0 nên hàm số nghịch biến trên R.
Bảng biến thiên
Đồ thị:
Cho x=0 thì y=2 ta được điểm (0;2).
Cho x=1 thì y=-1 ta được điểm (1;-1).
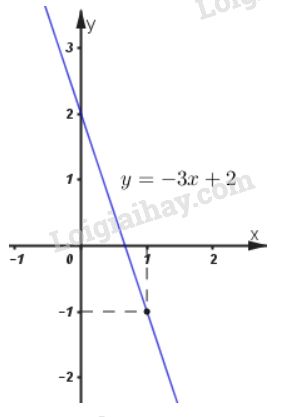
Đồ thị là đường thẳng đi qua \((0; 2)\) và \(({1; \, -1}).\)
LG b
\(y = 2x^2\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
- \frac{b}{{2a}} = 0\\
- \frac{\Delta }{{4a}} = 0
\end{array}\)
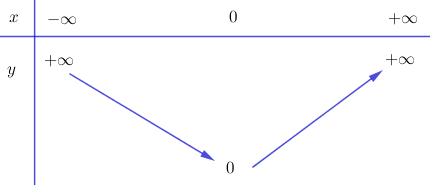
\(a=2>0\) nên hàm số đồng biến trên \(\left( {0; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;0} \right)\)
Bảng biến thiên:
Đồ thị:
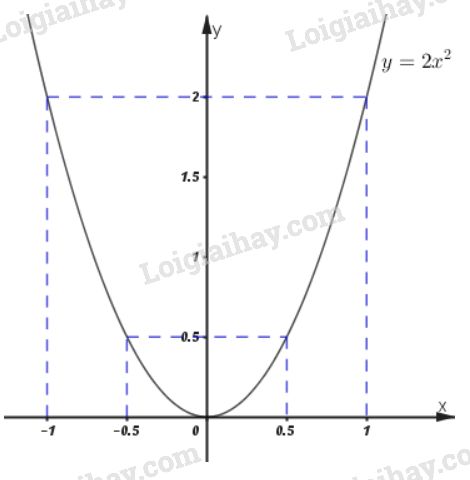
Đồ thị hàm số là Parabol:
- Đỉnh \(O(0;0)\)
- Đi qua các điểm \((0; \, 0), \, (-1; \, 2), \, (1;\, 2).\)
- Bề lõm hướng lên trên.
- Trục đối xứng \(Oy\).
LG c
\(y = 2x^2– 3x +1\)
Lời giải chi tiết:
Ta có: a=2, b=-3, c=1
\(\Delta = {b^2} - 4ac = {\left( { - 3} \right)^2} - 4.2.1 = 1\)
\(\begin{array}{l} - \dfrac{b}{{2a}} = - \dfrac{{ - 3}}{{2.2}} = \dfrac{3}{4}\\ - \dfrac{\Delta }{{4a}} = - \dfrac{1}{8}\end{array}\)
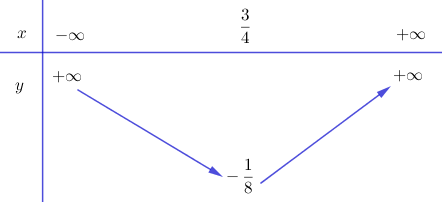
Vì \(a = 2 > 0\) nên hàm số nghịch biến trên khoảng \(\left( { - \infty ;\dfrac{3}{4}} \right)\) và đồng biến trên khoảng \(\left( {\dfrac{3}{4}; + \infty } \right)\).
Bảng biến thiên
Đồ thị:
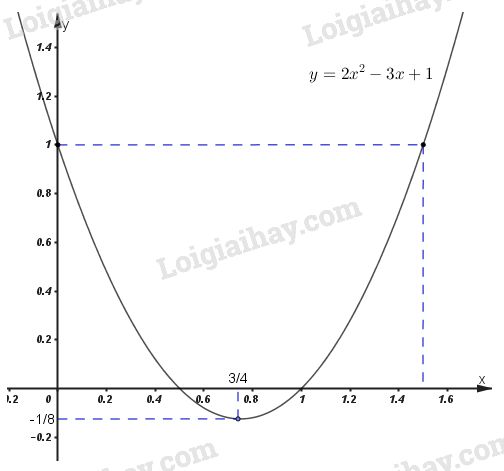
Đồ thị là parabol có đỉnh là \(I({3 \over 4},{{ - 1} \over 8})\), trục đối xứng \(x = {3 \over 4}\)
- Cắt trục tung tại \(P(0; 1)\), cắt trục hoành tại các điểm có hoành độ là nghiệm của phương trình:
\(2{x^2} - 3x + 1 = 0 \Leftrightarrow {x_1} = {1 \over 2},{x_2} = 1\)
tức là cắt trục hoành tại \(({1 \over 2},0)\) và \((1;0).\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3 trang 159 SGK Đại số 10
- Bài 4 trang 159 SGK Đại số 10
- Bài 5 trang 159 SGK Đại số 10
- Bài 7 trang 159 SGK đại số 10
- Bài 8 trang 159 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
