Bài 3 trang 159 SGK Đại số 10
Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình sau:
Đề bài
Phát biểu quy tắc xét dấu một nhị thức bậc nhất. Áp dụng quy tắc đó để giải bất phương trình sau:
\(\displaystyle f(x) = {{(3x - 2)(5 - x)} \over {(2 - 7x)}} \ge 0.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Quy tắc xét dấu một nhị thức dựa trên định lí :
“Nhị thức \(f(x) = ax + b (a≠0)\) có dấu cùng với hệ số \(a\) khi \(x\) lấy giá trị trong khoảng \(({{ - b} \over a}, + \infty )\) và trái dấu với hệ số \(a\) khi \(x\) lấy các giá trị thuộc khoảng \(( - \infty ,{{ - b} \over a})\)”.
Lời giải chi tiết
Ta có:
\(\begin{array}{l}
+ )\;3x - 2 = 0 \Leftrightarrow x = \frac{2}{3}.\\
+ )\;5 - x = 0 \Leftrightarrow x = 5.\\
+ )\;2 - 7x = 0 \Leftrightarrow x = \frac{2}{7}.
\end{array}\)
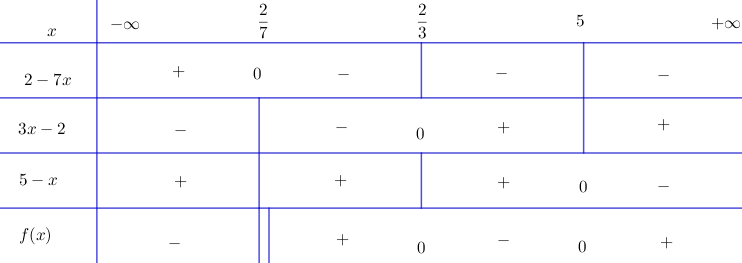
Áp dụng: Ta lập bảng xét dấu của vế trái \(f(x)\) của bất phương trình:
Tập nghiệm của bất phương trình: \(S = ({2 \over 7},{2 \over 3}{\rm{] }} \cup {\rm{ [}}5, + \infty )\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4 trang 159 SGK Đại số 10
- Bài 5 trang 159 SGK Đại số 10
- Bài 7 trang 159 SGK đại số 10
- Bài 8 trang 159 SGK Đại số 10
- Bài 1 trang 159 (Bài tập) SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
