Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 5. Tiên đề Ơ-clit về đường thẳng song song
Bài 34 trang 94 SGK Toán 7 tập 1
Dựa vào hình vẽ tính góc, so sánh 2 góc A và B, Tính góc B2.
Đề bài
Hình \(22 \) cho biết \(a // b\) và \(\widehat{A_{4}}=37^{\circ}\).
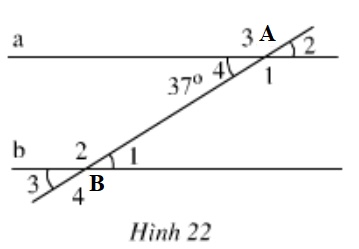
a) Tính \(\widehat{B_{1}}\).
b) So sánh \(\widehat{A_{1}}\) và \(\widehat{B_{4}}\).
c) Tính \(\widehat{B_{2}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng tính chất của hai đường thẳng song song: Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau.
b) Hai góc đồng vị bằng nhau.
c) Hai góc trong cùng phía bù nhau.
Lời giải chi tiết
a) Vì \(a//b\) nên \(\widehat{B_{1}}=\widehat{A_{4}}=37^{\circ}\) (hai góc so le trong)
b) Ta có: \(\widehat{A_{1}}\) và \(\widehat{A_{4}}\) là hai góc kề bù
nên \(\widehat{A_{1}}+\widehat{A_{4}}=180^{\circ}\)
\(\Rightarrow \widehat{A_{1}}=180^{\circ}-\widehat{A_{4}}\)
\(=180^{\circ}-37^{\circ}=143^{\circ}\)
\(a//b\) nên \(\widehat{A_{1}}=\widehat{B_{4}}=143^{\circ}\) (hai góc đồng vị).
c) Cách 1: \(\widehat{B_{2}}=\widehat{B_{4}}=143^{\circ}\) (hai góc đối đỉnh);
Cách 2: \(\widehat{A_{1}}=\widehat{B_{2}}=143^{\circ}\) (hai góc so le trong);
Cách 3: \(\widehat{B_{2}}+\widehat{A_{4}}=180^{\circ}\) (hai góc trong cùng phía bù nhau) nên \(\widehat{B_{2}}=180^{\circ}-\widehat{A_{4}}=180^{\circ}-37^{\circ}=143^{\circ}\)
Bình luận
Chia sẻ
- Bài 35 trang 94 SGK Toán 7 tập 1
- Bài 36 trang 94 SGK Toán 7 tập 1
- Bài 37 trang 95 SGK Toán 7 tập 1
- Bài 38 trang 95 SGK Toán 7 tập 1
- Bài 39 trang 95 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
