 Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
 Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đườn..
Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đườn..
Bài 14 trang 60 SGK Toán 7 tập 2
Vẽ tam giác PQR
Đề bài
Đố : Vẽ tam giác \(PQR\) có \(PQ = PR =5\,cm\), \(QR = 6\,cm\). Lấy điểm \(M\) trên đường thẳng \(QR\) sao cho \(PM = 4,5\,cm\). Có mấy điểm \(M\) như vậy ?
Điểm \(M\) có nằm trên cạnh \(QR\) hay không ? Tại sao ?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lý về quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu.
Lời giải chi tiết
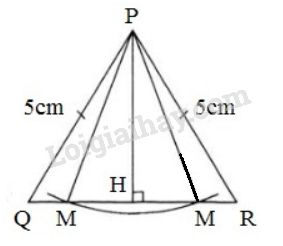
* Vẽ hình:
- Vẽ tam giác \(PQR\) có \(PQ = PR = 5\,cm,\; QR = 6\,cm\).
+ Vẽ đoạn thẳng \(QR = 6\,cm\).
+ Vẽ cung tròn tâm \(Q\) và cung tròn tâm \(R\) bán kính \(5\,cm\). Hai cung tròn này cắt nhau tại \(P\).
+ Nối \(PQ\) và \(PR\) ta được tam giác cần vẽ.
- Vẽ điểm \(M\): Vẽ cung tròn tâm \(P\) bán kính \(4,5\,cm\) cắt đường thẳng \(QR\) (nếu có) tại \(M\).
* Chứng minh
\(∆PQR\) có \(PQ = PR = 5\,cm\) nên \(∆PQR\) cân tại \(P\). Từ \(P\) kẻ đường thẳng \(PH ⊥ QR\).
Xét hai tam giác vuông tại H: \(ΔPHQ\) và \(ΔPHR\) có
\(PH\) chung
\(PQ = PR ( = 5cm)\)
\(⇒ ΔPHQ = ΔPHR\) (cạnh huyền – cạnh góc vuông)
\(⇒ HQ = HR\) (Hai cạnh tương ứng)
Mà \(HQ + HR = QR = 6 cm\)
Suy ra \(HQ=HR=QR:2=6:2=3cm\)
+ \(ΔPHR\) vuông tại H có \(PR^2= PH^2+ HR^2\) (định lí Py – ta – go)
\(⇒ PH^2= PR^2– HR^2= 5^2– 3^2= 16\)\( ⇒ PH = 4cm .\)
Đường vuông góc \(PH = 4cm\) là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.
Vậy chắc chắn có đường xiên \(PM = 4,5cm\) (vì \(PM = 4,5cm > 4cm)\) kẻ từ P đến đường thẳng QR.
Gọi \(M\) là một điểm nằm trên đường thẳng \(QR\).
Ta có: \(MH, QH, RH\) lần lượt là hình chiếu của \(PM, PQ, PR\) trên \(QR\).
Vì \(PM = 4,5\,cm < PQ\) (hoặc \(PR\)) nên \(MH < QH, MH < RH\).
- Tương tự trên \(RH \) có \(MH < RH\) nên \(M\) nằm giữa hai điểm \(R\) và \(H\).
Do vậy có hai điểm \(M\) thỏa mãn điều kiện đề bài và điểm \(M\) này nằm trên cạnh \(QR\).
Loigiaihay.com
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 3 – Hình học 7
>> Xem thêm












Danh sách bình luận