Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học
Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đườn..
Bài 13 trang 60 SGK Toán 7 tập 2
Hãy chứng minh rằng:
Đề bài
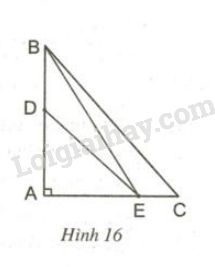
Cho hình 16. Hãy chứng minh rằng:
a) \(BE < BC\)
b) \(DE < BC\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;
a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Lời giải chi tiết
a) Trong hình vẽ \(BE\) và \(BC\) là hai đường xiên vẽ từ \(B\) đến đường \(AC\) và \(AE, AC\) lần lượt là hai hình chiếu của \(BE; \,BC\).
Vì \(AE < AC\) (vì E nằm giữa A và C) nên \(BE < BC\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
b) Vì \(EA \bot AB\) nên \(EB\) và \(ED\) là hai đường xiên vẽ từ \(E\) đến \(AB\) và \(AB, AD\) lần lượt là hai hình chiếu của \(EB;\;ED\).
Vì \(AD < AB\) (vì D nằm giữa A và B) nên \(DE < BE\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)
Ta có: \(BE < BC\) (câu a) và \(DE < BE\) nên \(DE < BC\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 14 trang 60 SGK Toán 7 tập 2
- Đề kiểm tra 15 phút - Đề số 1 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 3 - Bài 2 - Chương 3 – Hình học 7
- Đề kiểm tra 15 phút - Đề số 4 - Bài 2 - Chương 3 – Hình học 7
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
