Bài 10 trang 21 SGK Toán 11 tập 1 - Cánh diều

Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là (HK = 20m). Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C.

Đề bài

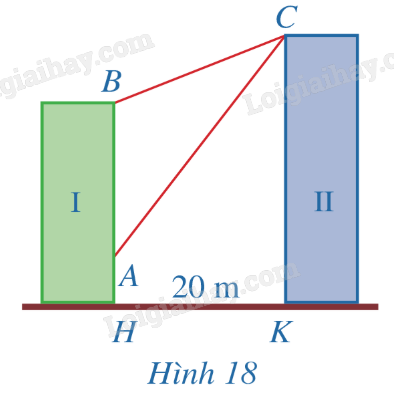
Có hai chung cư cao tầng I và II xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư II người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư I mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư I). Biết rằng chiều cao của chung cư II là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Phương pháp giải - Xem chi tiết

Dựa vào công thức cộng để tính.

Lời giải chi tiết

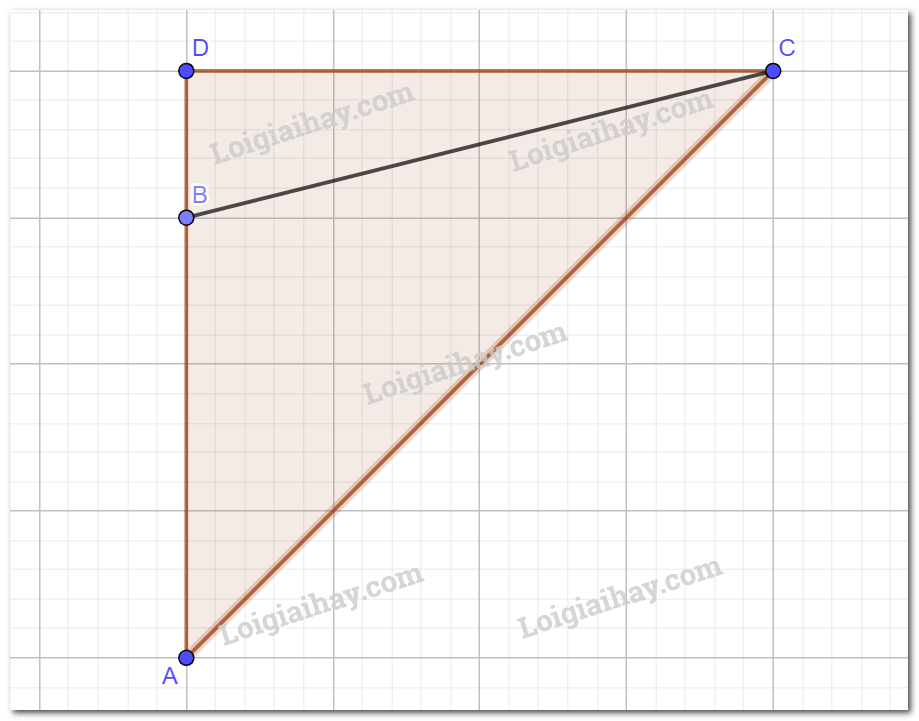
Từ C kẻ CD vuông góc với AB.

Ta có: \(AD = CK - AH = 32 - 6 = 26\left( m \right)\);

\(AB = BH - AH = 24 - 6 = 18\left( m \right)\);

\(DB = AD - AB = 26 - 18 = 8\left( m \right)\);

\(CD = HK = 20\left( m \right)\).

Ta có: \(\tan DCB = \frac{{DB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\).

\(\tan DCA = \frac{{DA}}{{DC}} = \frac{{26}}{{20}} = \frac{{13}}{{10}}\).

\(\tan BCA = \tan \left( {DCA - DCB} \right) \)

\(= \frac{{\tan DCA - \tan DCB}}{{1 + \tan DCA.\tan DCB}} = \frac{{\frac{{13}}{{10}} - \frac{2}{5}}}{{1 + \frac{{13}}{{10}}.\frac{2}{5}}} = \frac{{45}}{{76}}\).

\(\Rightarrow \widehat {ACB} \approx 30,6^\circ \).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 9 trang 21 SGK Toán 11 tập 1 - Cánh diều
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 17)
Bài 8 trang 21 SGK Toán 11 tập 1 - Cánh diều
Rút gọn biểu thức: (A = frac{{sin x + sin 2x + sin 3x}}{{cos x + cos 2x + cos 3x}})
Bài 7 trang 21 SGK Toán 11 tập 1 - Cánh diều
Cho (cos 2x = frac{1}{4}). Tính: (A = cos left( {x + frac{pi }{6}} right)cos left( {x - frac{pi }{6}} right));
Bài 6 trang 21 SGK Toán 11 tập 1 - Cánh diều
Cho (cos 2a = frac{1}{3}) với (frac{pi }{2} < a < pi ). Tính (sin a,,,cos a,,,tan a)
Bài 5 trang 20 SGK Toán 11 tập 1 - Cánh diều
Cho (sin a + cos a = 1). Tính: (sin 2a)
Bài 4 trang 20 SGK Toán 11 tập 1 - Cánh diều
Cho \(\sin a = \frac{2}{{\sqrt 5 }}\). Tính: \(\cos 2a,\,\cos 4a\)
Bài 3 trang 20 SGK Toán 11 tập 1 - Cánh diều
Cho (tan left( {a + b} right) = 3,,tan left( {a - b} right) = 2). Tính: (tan 2a,,,tan 2b)
Bài 2 trang 20 SGK Toán 11 tập 1 - Cánh diều
Tính \(A = \sin \left( {a - 17^\circ } \right)\cos \left( {a + 13^\circ } \right) - \sin \left( {a + 13^\circ } \right)\cos \left( {a - 17^\circ } \right)\)
Bài 1 trang 20 SGK Toán 11 tập 1 - Cánh diều
Cho (cos a = frac{3}{5}) với (0 < a < frac{pi }{2}). Tính: (sin left( {a + frac{pi }{6}} right),,cos left( {a - frac{pi }{3}} right),,tan left( {a + frac{pi }{4}} right))
Giải mục 4 trang 19, 20 SGK Toán 11 tập 1 - Cánh Diều
Sử dụng công thức biến đổi tích thành tổng và đặt (a + b = u;,,a - b = v) biến đổi các biểu thức sau thành tích: (cos u + cos v;,,cos u - cos v;,,sin u + sin v;,,sin u - sin v)
Giải mục 3 trang 18, 19 SGK Toán 11 tập 1 - Cánh Diều
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
Giải mục 2 trang 18 SGK Toán 11 tập 1 - Cánh Diều
Tính (sin 2a,,,cos 2a,,,tan 2a) bằng cách thay (b = a) trong công thức cộng.
Giải mục 1 trang 16, 17 SGK Toán 11 tập 1 - Cánh Diều
Cho tam giác MNP có đường cao PQ (Hình 17).
Lý thuyết Các phép biến đổi lượng giác - SGK Toán 11 Cánh Diều
I. Công thức cộng