Tổng hợp 20 đề thi học kì 1 Toán 7 kết nối tri thức có đáp án
Tải vềTổng hợp 20 đề thi học kì 1 Toán 7 kết nối tri thức có đáp án
Đề 1
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \( - 0,125?\)
A. \(\dfrac{1}{8}\) B. \( - \dfrac{1}{8}\) C. \( - \dfrac{1}{{125}}\) D. \(\dfrac{1}{{125}}\)
Câu 2: Kết quả của phép tính: \({\left( { - 0,08} \right)^4}{.10^4}\) là:
A. \(0,{8^4}\) B. \({8^4}\) C. \({10.8^4}\) D. \(0,{08^4}\)
Câu 3: So sánh \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \)?
A. \(2 + \sqrt {37} > 6 + \sqrt 2 \) B. \(2 + \sqrt {37} < 6 + \sqrt 2 \) C. \(2 + \sqrt {37} = 6 + \sqrt 2 \) D. Không có đáp án
Câu 4: Sắp xếp các số \(\left| { - 3} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\, - \dfrac{7}{3}\) theo thứ tự tăng dần.
A. \( - \dfrac{7}{3}\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| { - 3} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \) B. \( - \dfrac{7}{3}\,\,;\,\,\sqrt 6 \,;\,\,\left| { - 3} \right|\,\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \)
C. \(\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\,\,;\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\,\sqrt 6 \,\,;\,\, - \dfrac{7}{3}\,\,\) D. \( - \dfrac{7}{3}\,\,\,;\,\,\sqrt 6 \,\,;\,\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\)
Câu 5: Cho góc bẹt \(xOy\). Vẽ tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\). Vẽ tia \(Om\) là phân giác của góc \(xOz\). Vẽ tia \(On\) là tia phân giác của góc \(zOy\). Tính số đo góc \(mOn?\)
A. \(\angle mOn = {30^0}\) B. \(\angle mOn = {60^0}\) C. \(\angle mOn = {90^0}\) D. \(\angle mOn = {120^0}\)
Câu 6: Tính số đo của góc \(x\) trong hình vẽ dưới đây:
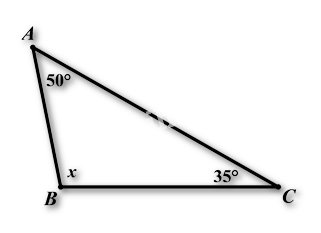
A. \(x = {85^0}\) B. \(x = {110^0}\) C. \(x = {115^0}\) D. \(x = {95^0}\)
Câu 7: Cho \(\Delta ABC = \Delta DEF.\) Biết \(\angle A = {33^0}\). Khi đó:
A. \(\angle D = {33^0}\) B. \(\angle D = {42^0}\) C. \(\angle E = {32^0}\) D. \(\angle D = {66^0}\)
Câu 8: Số tam giác cân trong hình vẽ dưới đây là:

A. \(2\) B. \(1\) C. \(4\) D. \(3\)
Câu 9: Đường trung trực của đoạn thẳng \(AB\) là đường thẳng …
A. song song với đoạn thẳng \(AB\).
B. vuông góc với đoạn thẳng \(AB\).
C. đi qua trung điểm của đoạn thẳng \(AB\).
D. vuông góc với đoạn thẳng \(AB\) tại trung điểm của nó.
Câu 10: Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
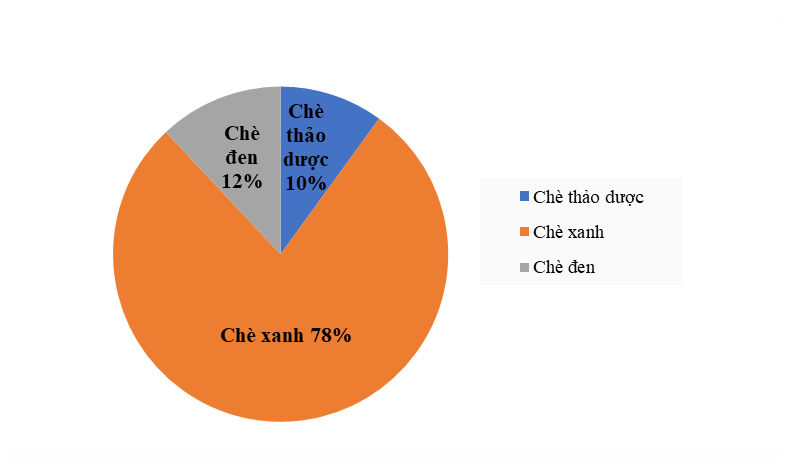
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm )
Thực hiện phép tính:
a) \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\) b) \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
c) \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\) d) \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}} \)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\) b) \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
c) \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\) d) \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
Bài 3: (1,0 điểm)
Tìm số đo của góc \(QRS\) trong hình vẽ bên dưới, biết \(aa'//bb'.\)
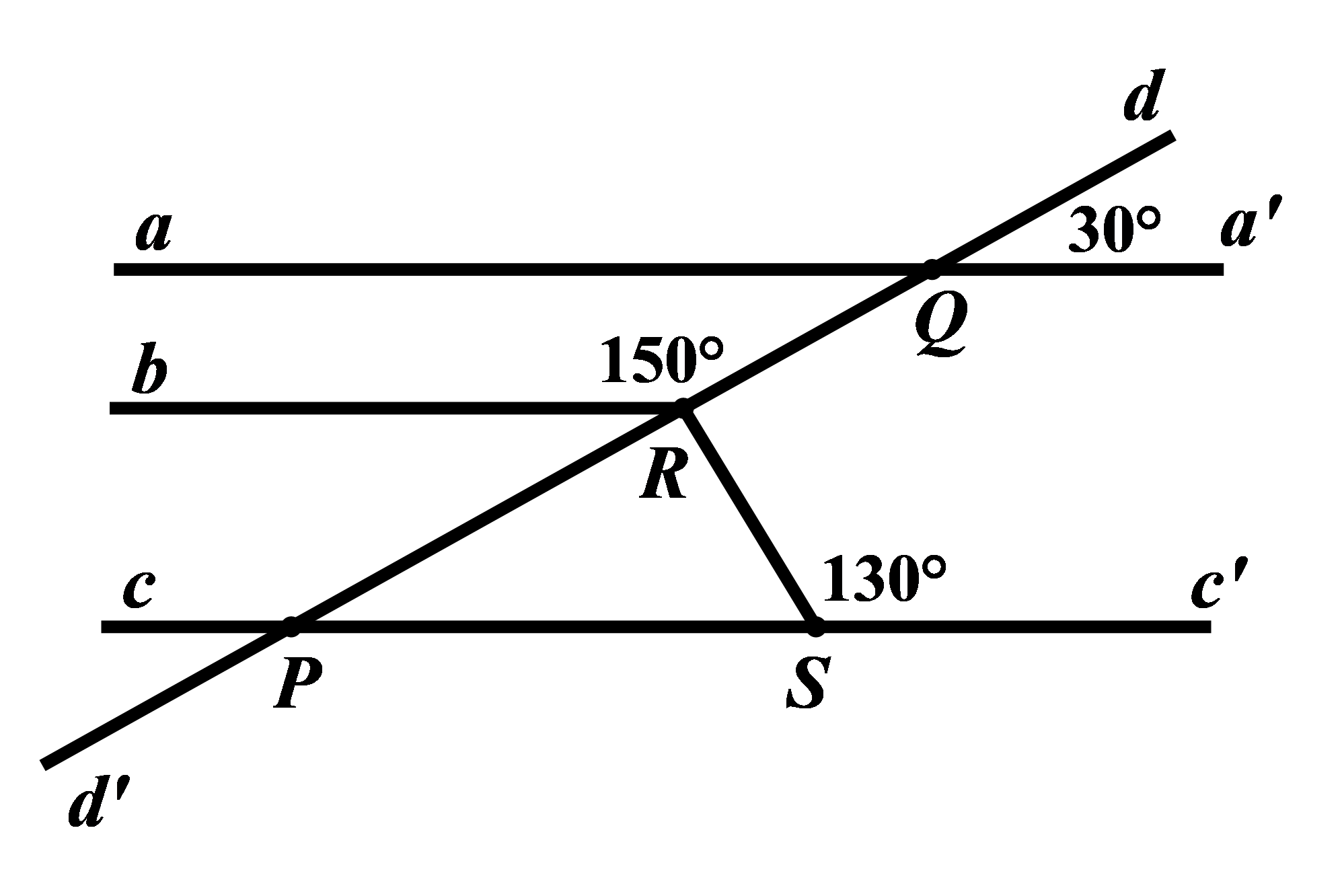
Bài 4: (1,5 điểm)
Cho tam giác \(ABC\) vuông tại \(A.\) Tia phân giác góc \(B\) cắt cạnh \(AC\) tại điểm \(M\). Vẽ \(MD\) vuông góc với \(BC\) (với \(D\) thuộc cạnh \(BC\)).
a) Chứng minh \(AB = BD\);
b) Gọi \(E\) là giao điểm của hai đường thẳng \(DM\) và \(AB\). Chứng minh \(\Delta ABC = \Delta DBE\).
Bài 5: (0,5 điểm)
Tìm số thực \(x\), biết: \(\left| x \right| + \left| {x + 2} \right| = 0\).
Đề 2
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Các số hữu tỉ \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\) được sắp xếp theo thứ tự tăng dần là:
A. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{3}{5}.\) B. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\frac{7}{5}.\)
C. \(\frac{{ - 5}}{{11}}\,\,;\,\,\frac{{ - 5}}{9}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{{18}}{{13}}\,\,;\,\,\frac{7}{5}.\) D. \(\frac{{ - 5}}{9}\,\,;\,\,\frac{{ - 5}}{{11}}\,\,;\,\,\frac{3}{5}\,\,;\,\,\frac{7}{5}\,\,;\,\,\frac{{18}}{{13}}.\)
Câu 2: Kết quả của phép tính: \(\frac{{{3^{10}}}}{{{5^{10}}}}{.5^{10}}\) là:
A. \({3^5}\) B. \({3^{20}}\) C. \({3^{10}}\) D. \({5.3^{10}}\)
Câu 3: Kết quả của phép tính: \(\sqrt {0,04} + \sqrt {0,25} + 2,31\) là:
A. \(2,53\) B. \(2,96\) C. \(2,6\) D. \(3,01\)
Câu 4: Cho \(x,y\) là hai số thực tùy ý. Khẳng định nào sau đây đúng?
A. \(\left| {x - y} \right| = x - y\) B. \(\left| {x - y} \right| = \left| x \right| - \left| y \right|\)
C. \(\left| {x + y} \right| = \left| x \right| + \left| y \right|\) D. \(\left| {x + y} \right| = \left| x \right| - \left| y \right|\) nếu \(x > 0 > y\) và \(\left| x \right| \ge \left| y \right|\)
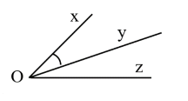
Câu 5: Quan sát hình vẽ bên dưới:
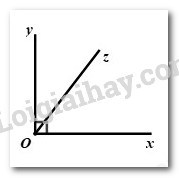
Tính số đo góc \(xOz\), biết \(\frac{1}{5}\angle xOz = \frac{1}{4}\angle yOz\).
A. \(\angle xOz = {40^0}\) B. \(\angle xOz = {50^0}\) C. \(\angle xOz = {30^0}\)\(\) D. \(\angle xOz = {60^0}\)
Câu 6: Tìm số đo của \(x\) trong hình vẽ dưới đây?

A. \(x = {55^0}\) B. \(x = {75^0}\) C. \(x = {60^0}\) D. \(x = {70^0}\)
Câu 7: Cho hai tam giác \(ABC\) và \(MNP\) có \(\angle ABC = \angle MNP,\angle ACB = \angle MPN\). Cần thêm một điều kiện để tam giác \(ABC\) và tam giác \(MNP\) bằng nhau theo trường hợp góc – cạnh – góc là:
A. \(AC = MP\) B. \(AB = MN\) C. \(BC = NP\) D. \(AC = MN\)
Câu 8: Quan sát hình vẽ bên dưới, tính số đo góc \(\angle ABH\) biết \(a//b\).

A. \(\angle ABH = {125^0}\) B. \(\angle ABH = {65^0}\) C. \(\angle ABH = {55^0}\) D. \(\angle ABH = {95^0}\)
Câu 9: Điền cụm từ còn thiếu vào …: “Định lí …”
A. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
B. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … thì ….
C. là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy….
D. là một câu nói được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng: Nếu … vậy ….
Câu 10: Biểu đồ đoạn thẳng trên cho biết nhiệt độ ở Hà Nội trong ngày 07/05/2021 tại một số thời điểm. Hãy cho biết thời điểm nào nhiệt độ thấp nhất, cao nhất?
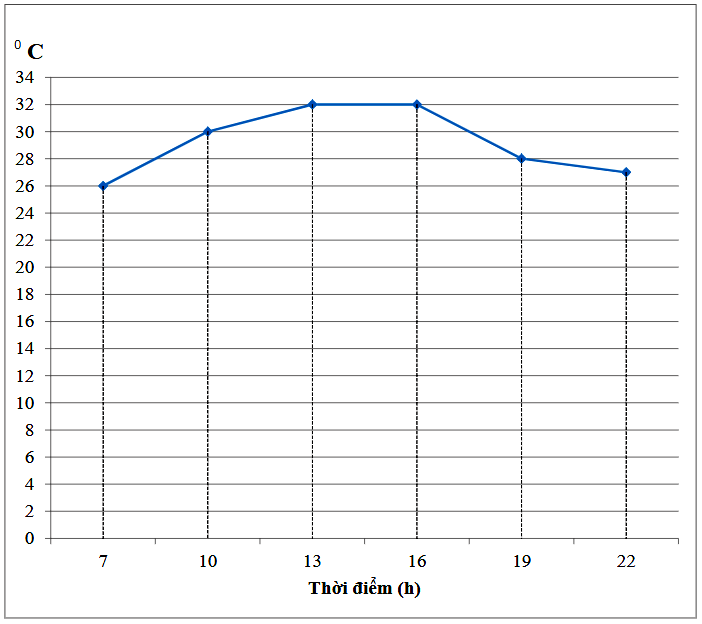
A. Thời điểm nhiệt độ thấp nhất là 26 độ C; thời điểm nhiệt độ cao nhất là 32 độ C.
B. Thời điểm nhiệt độ thấp nhất là 22 độ C; thời điểm nhiệt độ cao nhất là 32 độ C
C. Thời điểm nhiệt độ thấp nhất là 22 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
D. Thời điểm nhiệt độ thấp nhất là 7 giờ; thời điểm nhiệt độ cao nhất là 13 giờ đến 16 giờ.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(3,5.\frac{2}{{21}} - \frac{5}{9}:\frac{{25}}{3} + \frac{1}{{15}}\) b) \(16.{\left( {\frac{3}{{20}} - \frac{2}{5}} \right)^2} + \frac{3}{5}\)
c) \(\frac{{ - 11}}{3}:\left( {1,5.\sqrt {\frac{{16}}{9}} - \frac{{10}}{3}} \right)\) d) \(\left( {\sqrt {\frac{{81}}{{16}}} + \frac{{ - 3}}{4}} \right):{\left( { - \frac{3}{4}} \right)^2} - \left| {\frac{{ - 27}}{4}:{3^2}} \right|\)
Bài 2: ( 2 điểm) Tìm \(x\), biết:
a) \(\frac{1}{3}:x = 2\frac{2}{3}:\left( { - 0,3} \right)\) b) \({3^{2x}} - {2.3^5} = {3^5}\)
c) \(2x - \sqrt {1,69} = \sqrt {1,21} \) d) \(\left| {x + \frac{1}{3}} \right|.\left( {{x^2} + 1} \right) = 0\)
Bài 3: (1 điểm) Cho góc vuông \(uOv\) và tia \(Oy\) đi qua một điểm trong của góc đó. Vẽ tia \(Ox\) sao cho \(Ou\) là tia phân giác của góc \(xOy\). Vẽ tia \(Oz\) sao cho \(Ov\) là tia phân giác của góc \(yOz\). Chứng minh rằng hai góc \(xOy\) và \(yOz\) là hai góc kề bù.
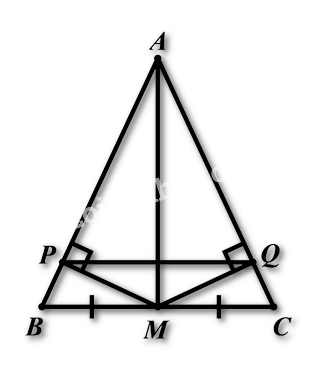
Bài 4: (1,5 điểm) Cho tam giác \(ABC\) cân tại đỉnh \(A\). Gọi \(M\) là trung điểm của \(BC\). Trên cạnh \(AB\) và \(AC\) lấy các điểm \(P,Q\) sao cho \(MP,MQ\) lần lượt vuông góc với \(AB,AC\).
a) Chứng minh rằng: \(MP = MQ\) và \(AP = AQ\).
b) Đường thẳng \(PQ\) có vuông góc với \(AM\) không? Vì sao?
Bài 5 (0,5 điểm): Tìm giá trị lớn nhất của biểu thức: \(A = - \sqrt {{x^2} + 81} + 2030.\)
Đề 3
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính: \(\dfrac{1}{2} + {\left[ {{{\left( { - 1103} \right)}^{1999}}} \right]^0}\) là:
A. \(\dfrac{1}{2}\) B. \(1\dfrac{1}{2}\) C. \(1\) D. \(\dfrac{{ - 1}}{2}\)
Câu 2: Số nào dưới đây là số vô tỉ?
A. \(\sqrt 7 \) B. \(1,\left( {01} \right)\) C. \(\sqrt {16} \) D. \(\dfrac{{ - 1}}{7}\)
Câu 3: Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thể giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 \({m^2}\). (Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
A. \(229,5m\) B. \(229m\) C. \(228,5m\) D. \(228m\)
Câu 4: Kết quả của phép tính: \(\left| {5 - \sqrt {45} } \right| + 15 - \sqrt {45} \) là:
A. \(10\) B. \(20 - 2\sqrt {45} \) C. \(20\) D. \(10 - \sqrt {45} \)
Câu 5: Tính số đo của góc \(x,y\) trong hình vẽ dưới đây:
A. \(x = {120^0},y = {30^0}\) B. \(x = {115^0},y = {35^0}\) C. \(x = {100^0},y = {50^0}\) D. \(x = {105^0},y = {45^0}\)
Câu 6: Quan sát hình vẽ sau:
Tính số đo của góc \(B\), biết \(\angle ACD = {30^0}\).
A. \({30^0}\) B. \({60^0}\) C. \({25^0}\) D. \({40^0}\)
Câu 7: Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM,\angle B = \angle P = {90^0}\). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông?
A. \(AB = PM\) B. \(AB = PN\) C. \(AC = MN\) D. \(\angle A = \angle N\)
Câu 8: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. Số học sinh xuất sắc chiếm \(14\% \), số học sinh giỏi chiếm \(14\% \).
B. Số học sinh xuất sắc chiếm \(16\% \), số học sinh giỏi chiếm \(16\% \).
C. Số học sinh xuất sắc chiếm \(15\% \), số học sinh giỏi chiếm \(15\% \).
D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{{ - 8}}{{19}}.\dfrac{{16}}{{31}} + \dfrac{{ - 8}}{{19}}.\dfrac{{15}}{{31}} - \dfrac{{11}}{{19}}\) b) \(\sqrt {{{\left( { - 5} \right)}^2}} .{\left( { - \dfrac{1}{5}} \right)^2}:\left[ {{{\left( {\dfrac{{ - 1}}{3}} \right)}^2} + \sqrt {\dfrac{1}{4}} - \sqrt {\dfrac{{16}}{9}} } \right]\)
c) \(\sqrt {121} - \sqrt {225} + \sqrt {\dfrac{{25}}{4}} \) d) \(\left| {\dfrac{{ - 11}}{3}} \right| + {\left( {\dfrac{{ - 1}}{2}} \right)^2} - \left| {4\dfrac{1}{2} + \left( { - 3,25} \right)} \right|\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( {3{x^2} + 1} \right)\left( {4x + \dfrac{1}{3}} \right) = 0\) b) \({\left( {x - \dfrac{3}{5}} \right)^2} = \dfrac{4}{3}:\dfrac{1}{3}\)
c) \(\left( {x + 2.\sqrt {16} } \right).\left| {2x + 3} \right| = 0\) d) \(\left| {x - \dfrac{2}{3}} \right| - 0,75 = 1\dfrac{1}{4}\)
Bài 3: (1,0 điểm) Trong hình vẽ bên dưới có \(BE//AC,CF//AB\). Biết \(\angle A = {80^0},\angle ABC = {60^0}.\)
a) Chứng minh rằng \(\angle ABE = \angle ACF\);
b) Tính số đo của các góc \(BCF\) và \(ACB\).
c) Gọi \(Bx,Cy\) lần lượt là tia phân giác của các góc \(ABE\) và \(ACF\). Chứng minh rằng \(Bx//Cy\).
Bài 4: (1,5 điểm) Cho tam giác \(ABC\) nhọn, lấy điểm \(M\) là trung điểm của cạnh \(AB\), lấy điểm \(N\) là trung điểm của cạnh \(AC\). Trên tia đối của tia \(NM\) lấy điểm \(Q\) sao cho \(NM = NQ\). Chứng minh rằng:
a) Hai tam giác \(AMN,CQN\) bằng nhau;
b) \(MB\) song song với \(QC\);
c) \(MN = \dfrac{1}{2}BC\).
Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức:
\(A = \sqrt {{{(x + 2)}^4} + 25} + {\left( {1 - y} \right)^2} - 999\)
Đề 4
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Phát biểu nào sau đây là sai?
A. Mọi số vô tỉ đều là số thực. B. Mọi số thực đều là số vô tỉ.
C. Số 0 là số hữu tỉ. D. \( - \sqrt 2 \) là số vô tỉ.
Câu 2: Một tam giác có độ dài cạnh \(\frac{2}{9}m\) và chiều cao ứng với cạnh đó bằng nửa cạnh đó. Tính diện tích của tam giác đã cho.
A. \(\frac{1}{9}{m^2}\) B. \(\frac{1}{{18}}{m^2}\) C. \(\frac{2}{{81}}{m^2}\) D. \(\frac{1}{{81}}{m^2}\)
Câu 3: Kết quả của phép tính: \(\left| {6 - \sqrt {34} } \right| + 3 + \sqrt {34} \) là:
A. \(9 + 2\sqrt {34} \) B. \(3 + 2\sqrt {34} \) C. \(9\) D. \(3\)
Câu 4: Cho biết \(1inch \approx 2,54cm\). Tính độ dài đường chéo bằng đơn vị một màn hình \(36inch\) và làm tròn đến hàng phần mười.
A. \(91,54\,cm\) B. \(91,5\,cm\) C. \(91,44\,cm\) D. \(91,4\,cm\)
Câu 5: Cho tam giác ABC có \(\widehat A = {98^0},\widehat C = {52^0}\). Số đo góc B là:
A.\({30^0}\) B.\({35^0}\) C. \({60^0}\) D. \({90^0}\)
Câu 6: Một tam giác cân có góc ở đỉnh bằng \({52^0}\) thì số đo góc ở đáy là:
A.\({54^0}\) B. \({64^0}\) C. \({72^0}\) D. \({90^0}\)
Câu 7: Ở hình vẽ bên dưới có \(AB\) và \(CD\) cắt nhau tại \(O,Ot\) là tia phân giác của góc \(BOC\)\(,\angle AOC - \angle BOC = {68^0}\). Số đo góc \(BOt\) là:
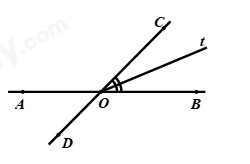
A. \({56^0}\) B. \({62^0}\)
C. \({28^0}\) D. \({23^0}\)
Câu 8: Cho hình vẽ bên dưới, biết hai đường thẳng \(m\) và \(n\) song song với nhau. Tính số đo góc \({B_4}?\)
A. \({80^0}\) B. \({100^0}\)
C. \({120^0}\) D. \({140^0}\)
Câu 9: Biểu đồ hình quạt tròn dùng để:
A. So sánh số liệu của hai đối tượng cùng loại.
B. So sánh các thành phần trong toàn bộ dữ liệu.
C. Biểu diễn sự thay đổi của một đại lượng theo thời gian.
D. Biểu diễn sự chênh lệch số liệu giữa các đối tượng.
Câu 10: Biểu đồ bên dưới biểu diễn thu nhập bình quân dầu người/năm của Việt Nam (tính theo đô la Mỹ) ở một số năm trong những gia đoạn từ 1986 đến 2020. Hãy cho biết năm nào Việt Nam có thu nhập cao nhất, cụ thể là bao nhiêu đô la?
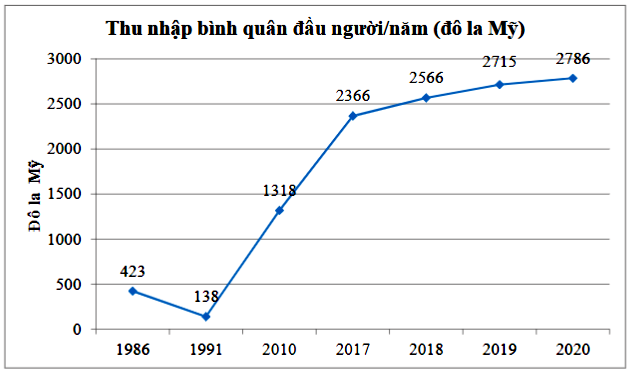
A. Năm 1991, Việt Nam có mức thu nhập thấp nhất là 138 đô la/năm.
B. Năm 2019, Việt Nam có mức thu nhập cao nhất là 2738 đô la/năm.
C. Năm 2018, Việt Nam có mức thu nhập cao nhất là 2566 đô la/năm.
D. Năm 2020, Việt Nam có mức thu nhập cao nhất là 2786 đô la/năm.
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Tính hợp lí (nếu có thể):
a) \(\frac{{ - 15}}{{14}}:\frac{{17}}{{23}} - \frac{{15}}{{14}}:\frac{{17}}{{11}} - \frac{6}{7}\) b) \(\left( {\frac{{ - 5}}{3} + \frac{{ - 3}}{2}} \right):\frac{{17}}{{13}} + \left( {\frac{7}{2} + \frac{{ - 1}}{3}} \right):\frac{{17}}{{13}}\)
c) \({3^2}.\frac{1}{{243}}{.81^2}.\frac{1}{{{3^3}}}\) d) \(\left( {{{4.2}^5}} \right):\left( {{2^3}.\frac{1}{{16}}} \right)\)
Bài 2: (1,5 điểm)
Tìm \(x\), biết:
a) \(\left( { - 0,2} \right) - x.\frac{1}{6} = \frac{2}{3}\)
b) \(5.\left( {\frac{1}{{\sqrt {25} }} - x} \right) - \sqrt {\frac{1}{{81}}} = \frac{{ - 1}}{9}\)
c) \(\left| x \right| = \frac{{13}}{{17}}\)
Bài 3: (2 điểm)
Cho tam giác ABC vuông tại A, có \(\widehat B = {60^0}\)và AB = 5cm. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC tại E.
a) Chứng minh: \(\Delta ABD{\rm{ }} = \Delta EBD.\)
b) Chứng minh: \(\Delta ABE\) là tam giác đều.
c) Tính độ dài cạnh BC.
Bài 4: (1 điểm)
Cho hình vẽ, biết \(Ax//By,\angle OAx = 35^\circ ,\angle OBy = 140^\circ \). Tính \(\angle AOB\)?
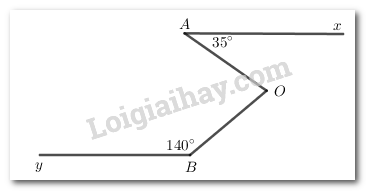
Bài 5: (0,5 điểm)
Tìm số nguyên \(x\) sao cho biểu thức sau là số nguyên: \(D = \frac{{\sqrt x + 2}}{{\sqrt x + 1}}\).
Đề 5
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Nếu \(\sqrt x = 3\)thì \({x^2}\) bằng bao nhiêu?
A. \(3\) B. \(6\) C. \(9\) D. \(81\)
Câu 2: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \(\dfrac{4}{{ - 5}}\)?
A. \(\dfrac{{12}}{{20}}\) B. \(\dfrac{{ - 12}}{{20}}\) C. \(\dfrac{{ - 24}}{{ - 30}}\) D. \(\dfrac{{ - 24}}{{30}}\)
Câu 3: Làm tròn số -2,13513 đến chữ số thập phân thứ hai có kết quả là:
A. \( - 2,13\) B. \( - 2,14\) C. \( - 2,1\) D. \(2,14\)
Câu 4: Tam giác ABC có \(\widehat A = 60^\circ ;\widehat B = 55^\circ \). Tính số đo góc ngoài tại đỉnh C của tam giác.
A. \(75^\circ \) B. \(115^\circ \) C. \(125^\circ \) D. \(85^\circ \)
Câu 5: Cho tam giác ABC và tam giác MNP có BC = PN, \(\widehat P = \widehat C\). Cần thêm một điều kiện nào nữa trong các điều kiện sau để \(\Delta ABC = \Delta MNP\) theo trường hợp góc – cạnh – góc ?
A.\(BA = NP\) B.\(\widehat B = \widehat N\) C. \(\widehat M = \widehat A\) D. \(AC = MN\)
Câu 6: Một tam giác cân có góc ở đáy bằng \({52^0}\) thì số đo góc ở đỉnh là:
A.\({52^0}\) B. \({76^0}\) C. \({72^0}\) D. \({90^0}\)
Câu 7: Cho hình vẽ, biết \(AE\,//\,BD,\,\angle ABD = {90^o},\,\angle AED = {55^o}.\) Số đo góc \(\angle BAE\) và \(\angle BDE\) lần lượt là:
A. \({90^o},\,{55^o}\) B. \({90^o},\,{125^o}\) C. \({55^o},\,{90^o}\) D. \({35^o},\,{55^o}\)
Câu 8: Kết quả của phép tính \(B = \left( { - \dfrac{3}{9}} \right).\dfrac{3}{{11}} - \dfrac{6}{9}.\dfrac{3}{{11}}\) là:
A. \(\dfrac{{ - 1}}{{11}}\). B. \(\dfrac{{ - 3}}{{11}}\). C. \(\dfrac{{ - 5}}{{11}}\). D. \(\dfrac{{ - 7}}{{11}}\).
Câu 9: Tìm \(x\) biết \(\dfrac{{12}}{{40}} - 2x = 0,\left( 1 \right) + {\left[ {1,\left( {24} \right)} \right]^0}\):
A. \(x = \dfrac{{ - 73}}{{180}}\). B. \(x = \dfrac{{ - 73}}{{90}}\). C. \(x = 0,4\). D. \(x = - 0,7\).
Câu 10: Cho biểu đồ đoạn thẳng. Em hãy cho biết nhu cầu bán máy tính để bàn, máy tính xách tay tăng hay giảm trong 6 tháng?
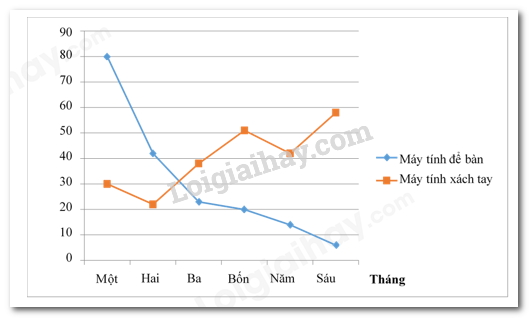
A. Máy tính để bàn tăng, máy tính xách tay tăng B. Máy tính để bàn tăng, máy tính xách tay giảm
C. Máy tính để bàn giảm, máy tính xách tay tăng D. Máy tính để bàn giảm, máy tính xách tay giảm
Phần II. Tự luận (7 điểm):
Bài 1: (1,5 điểm)
Tính giá trị của mỗi biểu thức sau:
a) \(1\dfrac{3}{4}.\dfrac{{ - 16}}{7}\)
b) \(12:\dfrac{{ - 6}}{5} + \dfrac{1}{5}\)
c) \(\dfrac{2}{{{3^2}}} + \dfrac{1}{3}:\left( {\dfrac{{ - 3}}{2}} \right) + \sqrt {\dfrac{1}{4}} .\left( { - 0,5} \right)\)
d) \({\left( {0,1} \right)^{21}}:{\left( { - 0,01} \right)^{10}}\)
Bài 2: (1,5 điểm)
Tìm \(x\), biết:
a) \(x - \dfrac{2}{5} = \dfrac{{ - 9}}{{10}}\)
b) \(\dfrac{3}{4} + \dfrac{1}{4}x = \dfrac{{ - 5}}{6}\)
c) \(\left| {x + \dfrac{1}{2}} \right| - \dfrac{1}{3} = 0\)
Bài 3: (3,5 điểm)
Cho tam giác ABC có AB = AC, M là trung điểm của BC.
a) Chứng minh rằng: \(\Delta AMB = \Delta AMC\)
b) Trên cạnh AB lấy điểm D. Từ D kẻ đường thẳng vuông góc với AM tại K và kéo dài cắt cạnh AC tại E. Chứng minh AD = AE.
c) Trên tia đối của tia ED lấy điểm F sao cho EF = MC, gọi H là trung điểm của EC. Chứng minh ba điểm M, H, F thẳng hàng.
Bài 4: (0,5 điểm)
Tìm số nguyên \(x\) sao cho biểu thức \(M = \dfrac{{5 - x}}{{x - 2}}\) đạt giá trị nhỏ nhất.
Đề 6
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Chọn phương án đúng?
A. \(\dfrac{1}{2} \notin \mathbb{Q}\) B. \(\dfrac{{ - 8}}{0} \in \mathbb{Q}\) C. \(5 \notin \mathbb{Q}\) D. \(\dfrac{4}{{ - 5}} \in \mathbb{Q}\)
Câu 2: Kết quả của phép tính: \({\left[ {{{\left( {0,3} \right)}^3}} \right]^4}.{\left( {0,3} \right)^3}\) là:
A. \({\left( {0,3} \right)^4}\) B. \({\left( {0,3} \right)^{10}}\) C. \({\left( {0,3} \right)^{15}}\) D. \({\left( {0,3} \right)^{12}}\)
Câu 3: Sắp xếp các số sau theo thứ tự tăng dần: \(2\dfrac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\)
A. \(2\dfrac{1}{4}\,\,;\,\,\sqrt {16} \,\,;\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,\,;\,\, - 0,0\left( {51} \right).\) B. \(\sqrt {16} \,\,;\,\,2\dfrac{1}{4}\,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,\,\, - \sqrt {83} \,\,;\, - \left| { - \sqrt {196} } \right|\,.\)
C. \( - \left| { - \sqrt {196} } \right|\,\,;\,\, - \sqrt {83} \,\,;\,\, - 0,0\left( {51} \right)\,\,;\,\,2\dfrac{1}{4}\,\,;\,\,\sqrt {16} .\) D. \(\sqrt {16} \,\,;\,\,2\dfrac{1}{4}\,\,;\,\,\, - 0,0\left( {51} \right)\,\,;\,\,\, - \sqrt {83} \,\,;\,\, - \left| { - \sqrt {196} } \right|\,.\)
Câu 4: Cho hình vẽ sau. Tính số đo \(\angle D\)?
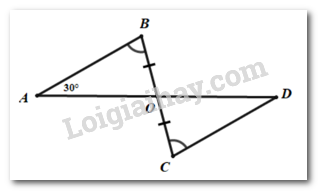
A. \(100^\circ \) B. \(50^\circ \) C. \(30^\circ \) D. \(70^\circ \)
Câu 5: Tam giác \(ABC\) có \(\angle A = {75^0};\angle B - \angle C = {25^0}\). Tính \(\angle C\)?
A. \(\angle C = {40^0}\) B. \(\angle C = {65^0}\) C. \(\angle C = {35^0}\) D. \(\angle C = {45^0}\)
Câu 6: Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
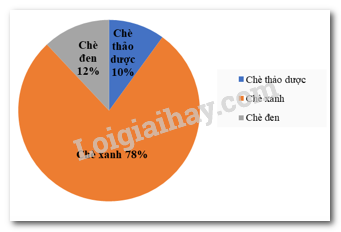
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
Câu 7: Cho biểu đồ sau:
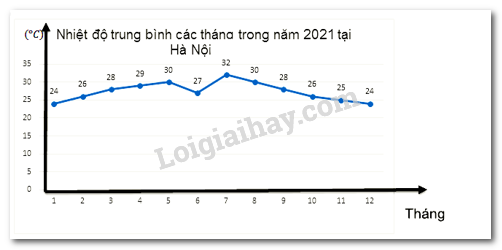
Hãy cho biết tiêu chí thống kê của biểu đồ trên là gì?
A. Tháng 1 đến tháng 12
B. Nhiệt độ trung bình các tháng trong năm 2021 tại Hà Nội
C. Nhiệt độ trung bình tại Hà Nội năm 2021 thay đổi theo thời gian
D. Nhiệt độ
Câu 8: Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = AC\). Qua \(A\) kẻ đường thẳng \(d\) cắt \(BC\). Vẽ \(BM,CN\) vuông góc với \(d\) với \(M,N \in d\). Chọn đáp án sai:
A. \(AM = CN\) B. \(BM = AN\) C. \(\angle ABM = \angle ACN\) D.\(\angle ABM = \angle CAN\)
Câu 9: Hai góc nào dưới đây là hai góc đối đỉnh?
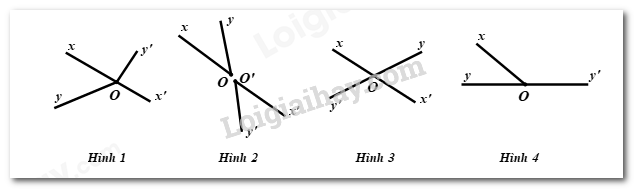
A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
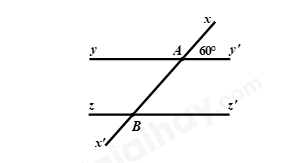
Câu 10: Cho hình vẽ bên dưới, biết \(yy'//zz',\angle xAy' = {60^0}\). Tính số đo của \(\angle zBx'.\)
A. \(\angle zBx' = {120^0}\) B. \(\angle zBx' = {80^0}\) C. \(\angle zBx' = {50^0}\) D. \(\angle zBx' = {60^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (1,5 điểm)
Thực hiện phép tính:
a) \(\left( {2\dfrac{5}{6} + 1\dfrac{4}{9}} \right):\left( {10\dfrac{1}{{12}} - 9,5} \right)\) b) \(\dfrac{{{{32}^3}{{.9}^5}}}{{{8^3}{{.6}^6}}}\)
c) \(\sqrt {64} + 2\sqrt {{{\left( { - 3} \right)}^2}} - 8.\sqrt {\dfrac{{25}}{{16}}} \) d) \(\left| {\dfrac{1}{{ - 5}}} \right| - \dfrac{{{{\left( { - 2} \right)}^2}}}{{\left| { - 5} \right|}} - \dfrac{{\left| 2 \right|}}{5}\)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(x - \dfrac{1}{2} = 3\dfrac{1}{2}:\dfrac{2}{7}\) b) \({3^{ - 1}}{.3^x} + {5.3^{x - 1}} = 162\) (\(x\) là số nguyên)
c) \(\sqrt {1,96} + 3\dfrac{x}{4} = \sqrt {0,04} + \dfrac{1}{4}.\sqrt {{{\left( {\dfrac{{89}}{5}} \right)}^2}} \) d) \(\left| {2x:\dfrac{4}{5} - \dfrac{{1,6}}{4}} \right| = \dfrac{7}{5}\)
Bài 3: (3 điểm)
Cho tam giác \(ABC\) có : \(AB = AC\) và \(M\) là trung điểm của \(BC\).
a) Chứng minh \(AM\) là tia phân giác của góc \(BAC\).
b) Chứng minh \(AM \bot BC\).
c) Qua \(C\) kẻ đường thẳng \(d\) song song với \(AB\) cắt tia \(AM\) tại \(N\). Chứng minh \(M\) là trung điểm của \(AN\).
Bài 4: (0,5 điểm)
Tìm số nguyên \(x\) sao cho biểu thức sau là số nguyên:
\(G = \dfrac{{\sqrt x + 5}}{{\sqrt x - 3}}\)
Đề 7
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số đối của \(\dfrac{{ - 7}}{{12}}\) là:
A. \(\dfrac{7}{{12}}\) B. \(\dfrac{7}{{ - 12}}\) C. \(\dfrac{{12}}{{ - 7}}\) D. \(\dfrac{{12}}{7}\)
Câu 2: Chọn khẳng định đúng.
A. \(\dfrac{{ - 37}}{{41}} > \dfrac{{23}}{{ - 17}}\) B. \({\left( {\dfrac{1}{3}} \right)^{12}} > {\left( {\dfrac{1}{3}} \right)^{10}}\) C. \({\left( {2,5} \right)^6} = {\left( {0,5} \right)^{12}}\) D. \({\left( {2,5} \right)^4} < {\left( { - 2,5} \right)^5}\)
Câu 3: Chọn đáp án sai. Nếu \(\sqrt x = \dfrac{2}{3}\) thì:
A. \(x = {\left( { - \dfrac{2}{3}} \right)^2}\) B. \(x = - {\left( { - \dfrac{2}{3}} \right)^2}\) C. \(x = \dfrac{4}{9}\) D. \(x = {\left( {\dfrac{2}{3}} \right)^2}\)
Câu 4: Trong các phát biểu sau, phát biểu nào sai?
A. Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.
B. Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.
C. Hai số đối nhau có giá trị tuyệt đối bằng nhau.
D. Giá trị tuyệt đối của một số thực luôn bằng chính nó.
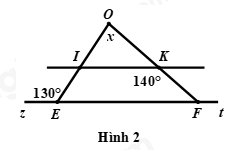
Câu 5: Quan sát Hình 2, có \(IK//EF\). Hãy tính giá trị của \(x\)?
A. \(x = {70^0}\) B. \(x = {110^0}\) C. \(x = {120^0}\) D. \(x = {90^0}\)
Câu 6:
Cho tam giác \(ABC\) có \(AB < AC\). Tia phân giác của góc \(A\) cắt \(BC\) ở \(K\). Từ \(B\) kẻ đường vuông góc với \(AK\) tại \(H\) cắt \(AC\) ở \(D\). Chọn câu sai.
A. \(HB = AD\) B. \(HB = HD\) C. \(AB = AD\) D. \(\widehat {ABH} = \widehat {ADH}\)
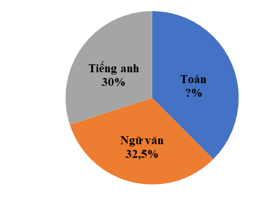
Câu 7: Số học sinh đăng ký học bổ trợ các Câu lạc bộ Toán, Ngữ văn, Tiếng anh của lớp 7 của một trường được biểu diễn qua biểu đồ hình quạt tròn như sau:
Tính số phần trăm học sinh đăng ký môn Toán là bao nhiêu?
A. 40% B. 37,5% C. 30% D. 35%
Câu 8: Cho biểu đồ biểu diễn chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:
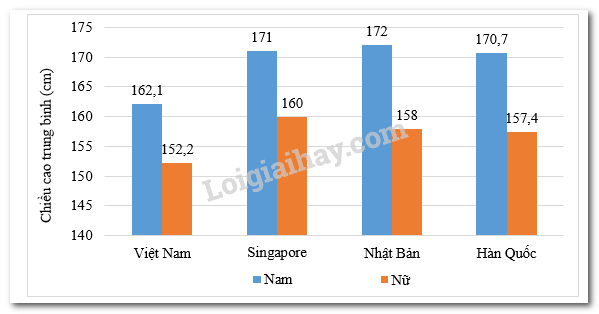
Sự chênh lệch chiều cao giữa nam và nữ của nước nào là lớn nhất?
- Việt Nam B. Singapore C. Nhật Bản D. Hàn Quốc
Câu 9: Phát biểu định lí sau bằng lời:
|
GT |
\(a//b,c \bot a\) |
|
KL |
\(c \bot b\) |
A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \({60^0}\).
D. Cả A, B, C đều đúng.
Câu 10: Vẽ \(\angle xOy = {50^0}\). Vẽ tia \(Om\) là tia phân giác của góc \(xOy\). Vẽ tia \(On\) là tia đối của tia \(Ox\). Tính góc \(mOn\).
A. \(\angle mOn = {125^0}\) B. \(\angle mOn = {155^0}\) C. \(\angle mOn = {160^0}\) D. \(\angle mOn = {175^0}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{7}{2}.\dfrac{{11}}{6} - \dfrac{7}{2}.\dfrac{5}{6}\)
b) \(\sqrt {36} - 3.\sqrt {\dfrac{1}{4}} + \left| {\dfrac{{ - 3}}{2}} \right|\)
c) \({\left( {\dfrac{{ - 1}}{2}} \right)^3} - \dfrac{7}{8}:\dfrac{7}{4} + \left| {\dfrac{{ - 9}}{8}} \right| + \sqrt {81} \)
Bài 2 (2,0 điểm). Tìm \(x\):
a) \(\dfrac{3}{5}x - \dfrac{6}{7} = \dfrac{1}{7}\)
b) \({\left( {2x - 1} \right)^3} = 64\)
c) \(2\left| {x + 1} \right| - 0,5 = \sqrt {\dfrac{1}{9}} \)
Bài 3: (3,5 điểm)
Cho góc nhọn \(xOy\), lấy điểm \(A\) trên tia \(Ox\) (điểm\(A\) khác \(O\)) và điểm \(B\) trên tia \(Oy\) sao cho \(OA = OB\). Gọi \(M\) là trung điểm của \(AB\).
a) Chứng minh: \(\Delta OAM = \Delta OBM\)
b) Trên tia \(OM\) lấy điểm \(H\) sao cho \(OM < OH\). Chứng minh \(HA = HB\).
c) Qua \(H\) kẻ đường thẳng song song với \(AB\) cắt \(Ox\) tại \(E\) cắt \(Oy\) tại \(K\). Chứng minh \(OH\) là đương trung trực của \(EK\).
d) Gọi giao điểm của \(AK\) và \(BE\) là \(N\). Chứng minh ba điểm \(O,M,N\) thẳng hàng.
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức \(A = {x^2} + 3\sqrt x - 2024\) với \(x \ge 0\).
Đề 8
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Nếu \(\sqrt x = 4\) thì x bằng
A. 2 B. 4 C. \( \pm \)2 D. 16
Câu 2: Tỉ lệ phần trăm số học sinh xuất sắc, giỏi, khá, trung bình của một lớp được biểu diễn qua biểu đồ hình quạt tròn sau:
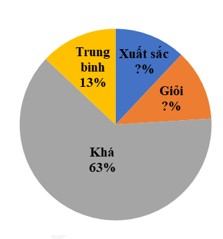
Tìm tỉ số phần trăm số học sinh xuất sắc và số hóc inh giỏi của lớp đó, biết rằng số học sinh xuất sắc bằng số học sinh giỏi.
A. Số học sinh xuất sắc chiếm \(14\% \), số học sinh giỏi chiếm \(14\% \).
B. Số học sinh xuất sắc chiếm \(16\% \), số học sinh giỏi chiếm \(16\% \).
C. Số học sinh xuất sắc chiếm \(15\% \), số học sinh giỏi chiếm \(15\% \).
D. Số học sinh xuất sắc chiếm \(12\% \), số học sinh giỏi chiếm \(12\% \).
Câu 3: Trong các phân số sau đây, phân số nào biểu diễn số hữu tỉ \(\dfrac{{ - 1}}{2}\).
A. \(\dfrac{{ - 2}}{4}\) B. \(\dfrac{{ - 22}}{{48}}\) C. \( - \dfrac{{ - 5}}{{10}}\) D. \(\dfrac{{ - 6}}{{18}}\)
Câu 4: Cách viết nào dưới đây là đúng?
A. \(\left| { - 0,55} \right| = 0,55\) B. \(\left| {0,55} \right| = - 0,55\) C. \(\left| { - 0,55} \right| = - 0,55\) D. \( - \left| {0,55} \right| = 0,55\)
Câu 5: Cho \(x = 6,67254\). Khi làm tròn đến chữ số thập phân thứ ba thì được kết quả là:
A. \(6,672\) B. \(6,672\) C. \(6,67\) D. \(6,6735\)
Câu 6: Kết quả của phép tính: \({\left( {\dfrac{1}{2}} \right)^2}.{\left( {\dfrac{1}{2}} \right)^3}\)bằng:
A. \({\left( {\dfrac{1}{2}} \right)^2}.\) B. \({\left( {\dfrac{1}{2}} \right)^5}\) C. \({\left( {\dfrac{1}{2}} \right)^3}\) D. \(\dfrac{1}{2}\)
Câu 7: Nếu \(\Delta ABC = \Delta DEF\) thì điều nào sau đây là không đúng?
A. \(\angle A = \angle E\) B. \(AB = DE\) C. \(BC = EF\) D. \(\angle C = \angle F\)
Câu 8: Cho a\( \bot \)b và b\( \bot \)c thì:
A. a // b B. a // c C. b // c D. a // b // c
Câu 9: Tam giác MNP có \(\angle M = {60^0}\), \(\angle N = {20^0}\), NK là tia phân giác. Số đo của góc \(\widehat {NKP}\) bằng:
A. 110 B. 100 C. 70 D. 30
Câu 10: Cho biểu đồ thể hiện tỉ lệ gia tăng dân số Việt Nam từ năm 1991 đến năm 2019 như dưới đây:
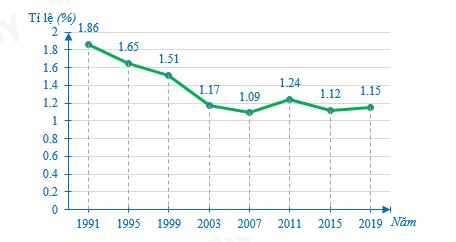
Tỉ lệ gia tăng dân số giai đoạn 1991 - 2007 tăng (hay giảm) bao nhiêu phần trăm?
A. Tăng 0,77%; B. Giảm 0,77%; C. Tăng 0,17%; D. Giảm 0,17%.
Phần II: Tự luận (7 điểm).
Câu 1: (2 điểm) Thực hiện phép tính:
a. \(\dfrac{2}{7} + \left( {\dfrac{{ - 17}}{7}} \right) + \dfrac{8}{7}\) b. \(\dfrac{5}{9}:\left( {\dfrac{1}{{11}} - \dfrac{5}{{22}}} \right) + \dfrac{5}{9}:\left( {\dfrac{1}{{15}} - \dfrac{2}{3}} \right).\)
c. \(\dfrac{{{{\left( { - 2} \right)}^3}}}{5}.\left| {\dfrac{1}{4} - 1} \right| + {2023^0}\). d. \( - \dfrac{5}{2}.\sqrt {\dfrac{9}{{25}}} - {2^2}.\left| { - \dfrac{1}{4}} \right|\)
Câu 2: (1,5 điểm) Tìm x
a. \(\,x + 1\dfrac{1}{2} = - 5,6\) b. \(\,\,\left| {x - \dfrac{1}{4}} \right| = \dfrac{5}{4}\) c. \({\left( {\dfrac{1}{5} - \dfrac{3}{2}x} \right)^2} = \dfrac{9}{4}\)
Câu 3: (3 điểm) Cho tam giác \(ABC\) vuông tại \(A\). Kẻ tia phân giác của \(\angle ABC\) cắt cạnh \(AC\) tại \(M\). Trên cạnh \(BC\) lấy điểm \(N\) sao cho \(BN = BA.\)
1) Chứng minh: \(\Delta BAM = \Delta BNM\).
2) Gọi \(I\) là giao điểm của \(BM\) và \(AN\). Chứng minh \(I\) là trung điểm của đoạn thẳng \(AN\).
3) Trên tia đối của tia \(AB\) lấy điểm \(K\) sao cho \(AK = NC\). Chứng minh \(\angle ABC = \angle NMC\) và \(K,M,N\) là ba điểm thẳng hàng.
Câu 4: (0,5 điểm) So sánh \({2^{30}} + {3^{30}} + {4^{30}}\) và \({3.24^{10}}\)
Đề 9
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Kết quả của phép tính: \(\left( {1 + 1\dfrac{1}{2}} \right):\dfrac{{ - 7}}{4}\) là:
A. \(\dfrac{{20}}{{ - 7}}\) B. \(\dfrac{{10}}{{ - 7}}\) C. \(\dfrac{{ - 5}}{{ - 14}}\) D. \(\dfrac{5}{{ - 7}}\)
Câu 2: Tìm \(x\), biết: \(x + \left( {\dfrac{1}{4}x - 2,5} \right) = \dfrac{{ - 11}}{{20}}\)
A. \(x = \dfrac{{39}}{{25}}\) B. \(x = \dfrac{{19}}{{20}}\) C. \(x = \dfrac{{17}}{{20}}\) D. \(x = \dfrac{{11}}{{25}}\)
Câu 3: Kết quả của biểu thức: \(2,8 + 3.\left| { - \dfrac{{13}}{3}} \right| + 0,2.\left| 6 \right| + 5.\left| {10} \right|\) là:
A. \(41\) B. \(53\) C. \(47\) D. \(67\)
Câu 4: Thứ tự tăng dần của các số: \(\sqrt {\dfrac{1}{{16}}} \,;\,4\dfrac{1}{7}\,;\,1,\left( 3 \right)\,;\,\sqrt {81} \,;\, - \sqrt {25} \,;\, - 12,1\) là:
A. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 5\,\,;\,\, - 12,1\) B. \(\sqrt {81} \,\,;\,\,4\dfrac{1}{7}\,\,;\,\,1,\left( 3 \right)\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\, - 12,1\,\,;\,\, - 5\)
C. \( - 12,1\,\,;\,\, - 5\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \) D. \( - 5\,\,;\,\, - 12,1\,\,;\,\,\sqrt {\dfrac{1}{{16}}} \,\,;\,\,1,\left( 3 \right)\,\,;\,\,4\dfrac{1}{7}\,\,;\,\,\sqrt {81} \)
Câu 5: Cho biểu đồ sau:
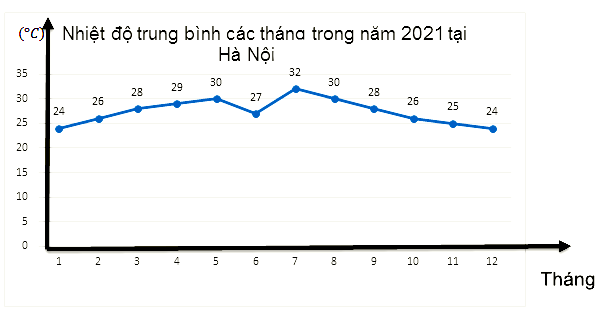
Tính nhiệt độ trung bình cả năm 2021.
A. 27 B. 27,4 C. 28 D. 28,4
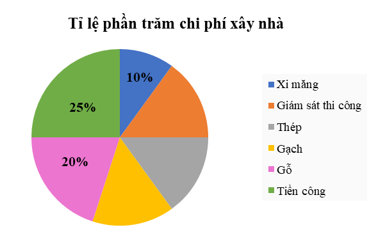
Câu 6: Chi phí xây dựng nhà được biểu diễn qua biểu đồ hình quạt tròn sau:
Tính số phần trăm chi phí gạch. Biết rằng chi phí giám sát thi công, thép, gạch bằng nhau.
A. \(15\% \) B. \(12\% \) C. \(20\% \) D. \(45\% \)
Câu 7: Cho hai góc kề bù \(AOB\) và \(BOC\). Tia \(OM\) nằm giữa hai tia \(OB\) và \(OC\). Tia \(ON\) là tia đối của tia \(OM\). Khi đó cặp góc đối đỉnh là cặp góc nào trong các góc sau đây?
A. \(\angle BOM\) và \(\angle CON\) B. \(\angle AOB\) và \(\angle AON\) C. \(\angle AOM\) và \(\angle CON\) D. \(\angle COM\) và \(\angle CON\)
Câu 8: Cho hình vẽ bên dưới. Biết \(AB//CD\)\(,\angle A = {70^0},\angle B = {60^0}.\) Tính số đo của góc \(ACB?\)
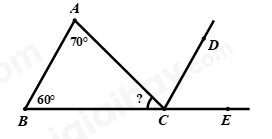
A. \(\angle ACB = {70^0}\) B. \(\angle ACB = {60^0}\) C. \(\angle ACB = {130^0}\) D. \(\angle ACB = {50^0}\)
Câu 9: Cho tam giác \(ABC\) vuông tại \(A\) và \(AB = AC\). Qua \(A\) kẻ đường thẳng \(d\) cắt \(BC\). Vẽ \(BM,CN\) vuông góc với \(d\) với \(M,N \in d\). Chọn đáp án sai:
A. \(AM = CN\) B. \(BM = AN\) C. \(\angle ABM = \angle ACN\) D.\(\angle ABM = \angle CAN\)
Câu 10: Tam giác \(ABC\) vuông tại \(A\) có \(\angle C = 30^\circ \). Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = AC\). Tính số đo \(\angle BDA\)?
A. \(70^\circ \) B. \(30^\circ \) C. \(90^\circ \) D. \(60^\circ \)
Phần II. Tự luận (7 điểm):
Bài 1: (1,5 điểm)
Thực hiện phép tính:
a) \(\left( { - \dfrac{1}{5} + \dfrac{3}{7}} \right):\dfrac{5}{4} + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{7}} \right):\dfrac{5}{4}\)
b) \(3.\sqrt {\dfrac{1}{9}} + 1,5.\sqrt {225} \)
c) \(\left( { - 1,5} \right) + 2.\left| {2\dfrac{1}{2}} \right| - 6.\left| {\dfrac{{ - 16}}{3}} \right| + 5.\left| { - 0,3} \right|\)
Bài 2: (1,5 điểm)
Tìm \(x\), biết:
a) \(x:\left( { - \dfrac{3}{5}} \right) = 1\dfrac{1}{4}\)
b) \({\left( {0,9} \right)^9}:x = - {\left( {0,9} \right)^7}\)
c) \(\left| {x - 12} \right| = \sqrt 5 - \sqrt 7 \)
Bài 3: (3,5 điểm) Cho tam giác \(ABC\) có \(AB < AC\). Tia phân goác của các góc \(BAC\) cắt \(BC\) tại \(D\). Trên cạnh \(AC\) lấy điểm \(M\) sao cho \(AM = AB.\)
a) Chứng minh \(\Delta ABD = \Delta AMD\)
b) Chứng minh \(DB = DM\) và \(\angle ABD = \angle AMD\).
c) Kéo dài \(AB\) và \(MD\) cắt nhau ở \(N\). Chứng minh \(\Delta BDN = \Delta MDC\).
d) Chứng minh \(AD\) vuông góc với \(BM\) và \(BM\) song song với \(NC\).
Bài 4: (0,5 điểm)
Với a,b là số thực dương thoả mãn \(ab + a + b = 1\). Chứng minh rằng: \(\sqrt {2\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)} = 2\left( {a + b} \right)\)
Đề 10
I. TRẮC NGHIỆM ( 3 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Trong các câu sau câu nào đúng?
A. \(\dfrac{3}{7} \in \mathbb{Q}\) B. \(\dfrac{1}{2} \in \mathbb{Z}\). C. \(\dfrac{{ - 9}}{5} \notin \mathbb{Q}\). D. \( - 6 \in \mathbb{N}\).
Câu 2: Tập hợp các số hữu tỉ kí hiệu là:
A. N; B. \({N^*}\) C. Q ; D. Z.
Câu 3: Số đối cùa \(\dfrac{{ - 2}}{3}\) là:
A. \(\dfrac{2}{3}\); B. \(\dfrac{3}{2}\); C. \(\dfrac{{ - 3}}{2}\) ; D. \(\dfrac{2}{{ - 3}}\).
Câu 4: Điểm B trên trục số biểu diễn số hữu tỉ nào sau đây?
A. \(\dfrac{{ - 2}}{3}\); B. \(\dfrac{{ - 2}}{5}\); C. \( - \dfrac{1}{3}\) ; D. \(\dfrac{2}{6}\).
Câu 5: Phép tính nào sau đây không đúng?
A. \({x^{18}}:{x^6} = {x^{12}}\left( {x \ne 0} \right)\); B. \({x^4}.{x^8} = {x^{12}}\)
C. \({x^2}.{x^6} = {x^{12}}\) D. \({({x^3})^4} = {x^{12}}\)
Câu 6: Cho các số sau \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3;\dfrac{5}{4} = 1,25\) số nào viết được dưới dạng số thập phân hữu hạn?
A. \(\dfrac{4}{6} = 0,66...6;\dfrac{{20}}{{15}} = 1,333....3\); B. \(\dfrac{3}{4} = 0,75;\dfrac{5}{4} = 1,25\);
C. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75\); D. \(\dfrac{4}{6} = 0,66...6;\dfrac{3}{4} = 0,75;\dfrac{{20}}{{15}} = 1,333....3\)
Câu 7: Cho tam giác \(ABC\) cân tại \(A\). Phát biểu nào trong các phát biểu sau là sai?
A. \(\angle B = \angle C\) B. \(\angle C = \dfrac{{180^\circ - \angle A}}{2}\) C. \(\angle A = 180^\circ - 2\angle C\) D. \(\angle B \ne \angle C\)
Câu 8: Chọn câu trả lời sai:
Biểu đồ đoạn thẳng biểu diễn sự thay đổi của một đối tượng theo thời gian thì:
A. Trục đứng biểu diễn đại lượng ta đang quan tâm
B. Trục ngang biểu diễn thời gian;
C. Trục đứng biểu diễn các tiêu chí thống kê
D. Các đoạn thẳng nối nhau tạo thành một đường gấp khúc.
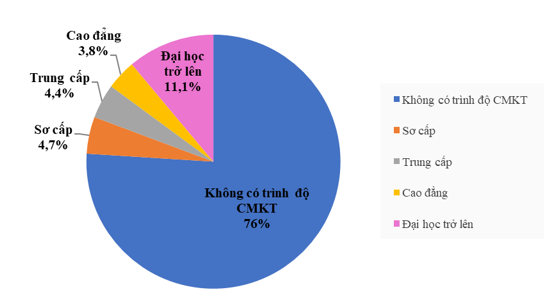
Câu 9: Biểu đồ hình quạt tròn bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) lực lượng lao động (từ 15 tuổi trở lên) phân theo trình độ chuyên môn kĩ thuật (CMKT) của nước ta (năm 2020).
Trong năm 2020, lực lượng lao động không có trình độ CMKT gấp bao nhiêu lần lực lượng lao động có trình độ đại học trở lên (làm tròn đến hàng phần mười)?
A. 6,7 B. 6,8 C. 6,9 D. 7
Câu 10: Tiên đề Euclid được phát biểu: “ Qua một điểm M nằm ngoài đường thẳng a. ”
A. Có duy nhất một đường thẳng đi qua M và song song với a.
B. Có hai đường thẳng song song với a.
C. Có ít nhất một đường thẳng song song với a.
D. Có vô số đường thẳng song song với a.
Câu 11: Nếu \(\Delta ABC = \Delta DEF\) và \(\angle B = {70^0};\angle F = {40^0}\) thì góc \(A\) bằng:
A. \({110^0}\) B. \({70^0}\) C. \({30^0}\) D. \({40^0}\)
Câu 12: Cho hình vẽ, biết\(\widehat {\;xOy} = {20^0}\), Oy là tia phân giác của góc \(\widehat {xOz}\). Khi đó số đo \(\widehat {yOz\;}\)bằng:
A. \({20^0}\) B. \(\;{160^0}\) C. \({80^0}\) D. \(\;{40^0}\).
II. TỰ LUẬN (7 điểm)
Câu 1: (2 điểm) Tính:
a) \(\sqrt 9 - \dfrac{2}{3}\)
b) \( - 5 + \sqrt {25} + {2023^0}\)
c) \({\left( {\dfrac{1}{4}} \right)^2} \cdot {\left( {\dfrac{1}{2}} \right)^5}:2\)
d) \(\left( {2,5 + \dfrac{2}{3}} \right) - 3\dfrac{1}{3}\)
Câu 2: (1,5 điểm) Tìm x:
a) \(2x - 3,7 = 10\)
b) \(\sqrt {49} + 5x - 1 = {\left( { - 2} \right)^3}\)
c) \(\dfrac{8}{3}.|2x + 1| = 3\dfrac{1}{3}\)
Câu 3: (3,0 điểm)
Cho tam giác \(ABC\) vuông tại \(A,M\) là trung điểm của \(AC\). Trên tia đối của tia \(MB\) lấy điểm \(K\) sao cho \(BM = MK.\)
a) Chứng minh: \(\Delta ABM = \Delta CKM\);
b) Chứng minh: \(BC = AK\);
c) Chứng minh: \(CK \bot AC\).
Câu 4: (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức \(M = \sqrt {{x^2} + 169} - 2024\).
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay














Danh sách bình luận