-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Các hình khối trong thực tiễn
-
Chương 4: Góc và đường thẳng song song
-
Chương 5: Một số yếu tố thống kê
-
Chương 6: Các đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số
-
Chương 8: Tam giác
- Bài 1: Góc và cạnh của một tam giác
- Bài 2: Tam giác bằng nhau
- Bài 3: Tam giác cân
- Bài 4: Đường vuông góc và đường xiên
- Bài 5: Đường trung trực của một đoạn thẳng
- Bài 6: Tính chất ba đường trung trực của tam giác
- Bài 7: Tính chất ba đường trung tuyến của tam giác
- Bài 8: Tính chất ba đường cao của tam giác
- Bài 9: Tính chất ba đường phân giác của tam giác
-
Chương 9: Một số yếu tố xác suất
Trắc nghiệm Bài 5: Đường trung trực của một đoạn thẳng Toán 7 Chân trời sáng tạo
Đề bài
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
-
A.
Hình chữ nhật
-
B.
Hình vuông
-
C.
Hình thoi
-
D.
Hình bình hành
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Khẳng định nào sau đây là đúng?
-
A.
IH = IK
-
B.
IH = IL
-
C.
IH +IK = IL
-
D.
IK = IL
Lời giải và đáp án
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
-
A.
Hình chữ nhật
-
B.
Hình vuông
-
C.
Hình thoi
-
D.
Hình bình hành
Đáp án : C
Sử dụng tính chất đường trung trực của đoạn thẳng.
Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.
Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)
Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)
Xét tam giác AOM và AON có:
OM = ON
\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)
AO chung
\( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c)
\( \Rightarrow \) AM = AN ( 2 cạnh tương ứng)
Mà MA = MB; NA = NB
\( \Rightarrow \) MA = MB = NB = NA
\( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Khẳng định nào sau đây là đúng?
-
A.
IH = IK
-
B.
IH = IL
-
C.
IH +IK = IL
-
D.
IK = IL
Đáp án : A
Dựa vào tính chất tam giác cân
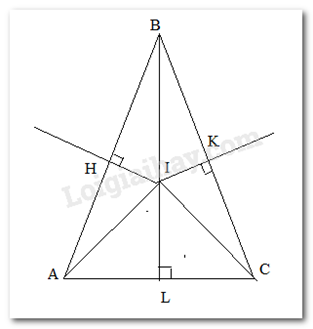
Vì tam giác ABC cân tại B nên BA = BC
Mà H, K lần lượt là trung điểm của BA và BC nên BH = BK
Xét tam giác vuộng BHI và BKI có:
BI chung
BH = BK
\( \Rightarrow BHI = \Delta BKI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) IH = IK (hai cạnh tương ứng).
Luyện tập và củng cố kiến thức Bài 6: Tính chất ba đường trung trực của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Tính chất ba đường trung tuyến của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Tính chất ba đường cao của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Tính chất ba đường phân giác của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Đường vuông góc và đường xiên Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Tam giác cân Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tam giác bằng nhau Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Góc và cạnh của một tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 3: Đại lượng tỉ lệ nghịch Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Đại lượng tỉ lệ thuận Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Làm quen với biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
Danh sách bình luận