-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Các hình khối trong thực tiễn
-
Chương 4: Góc và đường thẳng song song
-
Chương 5: Một số yếu tố thống kê
-
Chương 6: Các đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số
-
Chương 8: Tam giác
- Bài 1: Góc và cạnh của một tam giác
- Bài 2: Tam giác bằng nhau
- Bài 3: Tam giác cân
- Bài 4: Đường vuông góc và đường xiên
- Bài 5: Đường trung trực của một đoạn thẳng
- Bài 6: Tính chất ba đường trung trực của tam giác
- Bài 7: Tính chất ba đường trung tuyến của tam giác
- Bài 8: Tính chất ba đường cao của tam giác
- Bài 9: Tính chất ba đường phân giác của tam giác
-
Chương 9: Một số yếu tố xác suất
Trắc nghiệm Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác Toán 7 Chân trời sáng tạo
Đề bài
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh song song với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Các cạnh bên của hình lăng trụ đứng
-
A.
Song song với nhau
-
B.
Bằng nhau
-
C.
Vuông góc với hai đáy
-
D.
Có cả ba tính chất trên
Các mặt bên của hình lăng trụ đứng là
-
A.
Các hình bình hành
-
B.
Các hình thang cân
-
C.
Các hình chữ nhật
-
D.
Các hình vuông
Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
-
A.
9
-
B.
6
-
C.
12
-
D.
8
Phát biểu nào sau đây là đúng?
-
A.
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
-
B.
Các mặt bên của hình lăng trụ đứng là các hình thang cân.
-
C.
Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
-
D.
Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Lời giải và đáp án
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh song song với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Đáp án: C
Sử dụng quan hệ song song giữa đường thẳng và mặt phẳng.
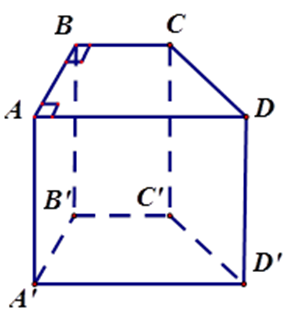
Vì $AA'{\rm{//}}BB'{\rm{//}}DD'$ và \(A'D'{\rm{//}}AD{\rm{//}}BC\) nên các đường thẳng $AA',DD',AD,A'D'$ song song với mp $\left( {BCC'B'} \right).$
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(5\)
Đáp án: B
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng.
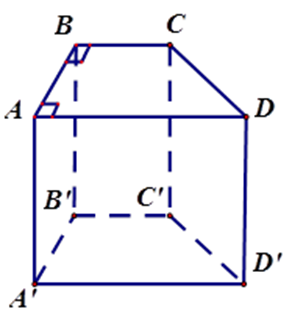
Vì \(AB \bot BC\) (do \(ABCD\) là hình thang vuông) và \(AB \bot BB'\) (tính chất lăng trụ đứng)
Nên \(AB \bot \left( {BCC'B'} \right)\) , tương tự ta có \(A'B' \bot \left( {BCC'B'} \right)\)
Do đó $AB,A'B'$ vuông góc với mp $\left( {BCC'B'} \right).$
Các cạnh bên của hình lăng trụ đứng
-
A.
Song song với nhau
-
B.
Bằng nhau
-
C.
Vuông góc với hai đáy
-
D.
Có cả ba tính chất trên
Đáp án : D
Hình lăng trụ đứng có các mặt bên là hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau.
Các mặt bên của hình lăng trụ đứng là
-
A.
Các hình bình hành
-
B.
Các hình thang cân
-
C.
Các hình chữ nhật
-
D.
Các hình vuông
Đáp án : C
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
-
A.
9
-
B.
6
-
C.
12
-
D.
8
Đáp án : A
Đặc điểm hình lăng trụ đứng tam giác
Các cạnh của hình lăng trụ đứng tam giác là: \(AB,\,\,AC,\,\,BC,\,\,{A_1}{B_1},\)\({A_1}{C_1},\,\,{B_1}{C_1},\,\,A{A_1},\,\,\,B{B_1},\,C{C_1}\)
Vậy hình lăng trụ đứng tam giác có tất cả \(9\) cạnh.
Phát biểu nào sau đây là đúng?
-
A.
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
-
B.
Các mặt bên của hình lăng trụ đứng là các hình thang cân.
-
C.
Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
-
D.
Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Đáp án : A
Đặc điểm hình lăng trụ đứng tam giác
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Luyện tập và củng cố kiến thức Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật - Hình lập phương Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Hình hộp chữ nhật - Hình lập phương Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 3: Đại lượng tỉ lệ nghịch Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Đại lượng tỉ lệ thuận Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Làm quen với biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
