Bài tập trắc nghiệm Toán 7 - Chân trời sáng tạo có đáp án Bài tập trắc nghiệm Chương 3: Các hình khối trong thực ..

Trắc nghiệm Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật - Hình lập phương Toán 7 Chân trời sáng tạo

Làm bài tập

Đề bài

Câu 1 :

Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:

A.

${a^2}$
B.

$4{a^2}$
C.

$2{a^4}$
D.

${a^3}$

Câu 2 :

Hãy chọn câu đúng. Cạnh của một hình lập phương bằng $5\,cm$ khi đó thể tích của nó là:

A.

$25c{m^3}$
B.

$50c{m^3}$
C.

$125c{m^3}$
D.

$625c{m^3}$

Câu 3 :

Các kích thước của hình hộp chữ nhật $ABC{\rm{D}}.A'B'C'D'$ là $DC = 6cm$ , $CB = 3cm$ . Hỏi độ dài của $A'B'$ và $AD$ là bao nhiêu $cm$ ?

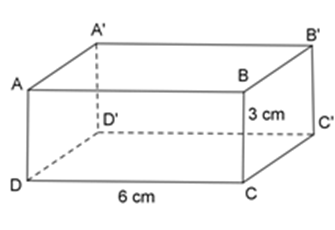
A.

$3\,cm$ và $6\,cm$
B.

$6\,cm$ và $9\,cm$
C.

$6\,cm$ và $3\,cm$
D.

$9\,cm$ và $6\,cm$

Câu 4 :

Một bể nước dạng hình hộp chữ nhật có kích thước các số đo trong lòng bể là: dài $4$ m, rộng $3$ m, cao $2,5$ m. Biết $\dfrac{3}{4}$ bể đang chứa nước. Hỏi thể tích phần bể không chứa nước là bao nhiêu?

A.

$30{m^3}$
B.

$22,5{m^3}$
C.

$7,5{m^3}$
D.

$5,7{m^3}$

Câu 5 :

Hình lập phương $A$ có cạnh bằng $\dfrac{2}{3}$ cạnh hình lập phương $B$ . Hỏi thể tích hình lập phương $A$ bằng bao nhiêu phần thể tích hình lập phương $B$ .

A.

$\dfrac{2}{9}$
B.

$\dfrac{{27}}{8}$
C.

$\dfrac{8}{{27}}$
D.

$\dfrac{4}{9}$

Câu 6 :

Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là $1440\,c{m^2}.$ Tính thể tích của hình lập phương đó.

A.

$1782\,c{m^3}$
B.

$1728\,c{m^3}$
C.

$144\,c{m^2}$
D.

$1827\,c{m^3}$

Câu 7 :

Một người thuê sơn mặt trong và mặt ngoài của $1$ cái thùng sắt không nắp dạng hình lập phương có cạnh $0,8$ m. Biết giá tiền mỗi mét vuông là $15000$ đồng. Hỏi người ấy phải trả bao nhiêu tiền?

A.

$86000$ đồng
B.

$69000$ đồng
C.

$96600$ đồng
D.

$96000$ đồng

Câu 8 :

Một căn phòng dài 4,5 m, rộng 3,8 m và cao 3,2 m. Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là $5,8{m^2}$. Diện tích cần quét vôi là:

A.

64,42 m²
B.

47,32 m²
C.

48,92 m²
D.

53,12 m²

Câu 9 :

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Diện tích các mặt $ABCD,\,\,BCC'B'$và $DCC'D'$lần lượt là $108c{m^2},72c{m^2}$và $96c{m^2}$. Tính thể tích của hình hộp

A.

276 cm³
B.

864 cm³
C.

864 cm²
D.

276 cm²

Câu 10 :

Hình hộp chữ nhật với ba kích thước lần lượt là a, 2a, 4a thì có thể tích là

A.

a³ ( đvtt)
B.

2a³ ( đvtt)
C.

8a³ ( đvtt)
D.

8a² ( đvdt)

Câu 11 :

Cho hình hộp chữ nhật có chiều dài bằng $6cm$, chiều rộng bằng $\frac{1}{3}$chiều dài và chiều cao gấp 4 lần chiều rộng. Thể tích của hình hộp chữ nhật đó là

A.

$216c{m^3}$
B.

$81c{m^3}$
C.

288 cm³
D.

96 cm³

Câu 12 :

Cho hình lập phương $ABC{\rm{D}}.A'B'C'D'$ có độ dài cạnh hình lập phương là 4 cm. Hỏi thể tích hình lập phương là bao nhiêu?

A.

16 cm³
B.

4 cm³
C.

32 cm³
D.

64 cm³

Câu 13 :

Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 80 cm, chiều rộng 50 cm, chiều cao 50 cm. Mực nước trong bể cao 25 cm. Người ta cho vào bể một hòn đá có thể tích tăng 20000 cm³. Hỏi mực nước trong bể lúc này cao bao nhiêu?

A.

40 cm
B.

30 cm
C.

60 cm
D.

50 cm

Câu 14 :

Một người thuê sơn mặt trong và mặt ngoài của 1 cái thùng sắt không nắp dạng hình lập phương có cạnh 0,8 m. Biết giá tiền mỗi mét vuông là 16000 đồng. Hỏi người ấy phải trả bao nhiêu tiền?

A.

96 000 đồng
B.

61 440 đồng
C.

102 400 đồng
D.

122 880 đồng

Lời giải và đáp án

Câu 1 :

Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:

A.

${a^2}$
B.

$4{a^2}$
C.

$2{a^4}$
D.

${a^3}$

Đáp án : D

Phương pháp giải :

Sử dụng công thức thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)

Lời giải chi tiết :

Thể tích của hình hộp chữ nhật là $V = a.2a.\dfrac{a}{2} = {a^3}$ (đvtt)

Câu 2 :

Hãy chọn câu đúng. Cạnh của một hình lập phương bằng $5\,cm$ khi đó thể tích của nó là:

A.

$25c{m^3}$
B.

$50c{m^3}$
C.

$125c{m^3}$
D.

$625c{m^3}$

Đáp án : C

Phương pháp giải :

Áp dụng công thức tính thể tích hình lập phương cạnh a là $V = {a^3}.$

Lời giải chi tiết :

Thể tích hình lập phương cạnh $5\,cm^3$ là:

$V = {5^3} = 125\;c{m^3}$

Câu 3 :

Các kích thước của hình hộp chữ nhật $ABC{\rm{D}}.A'B'C'D'$ là $DC = 6cm$ , $CB = 3cm$ . Hỏi độ dài của $A'B'$ và $AD$ là bao nhiêu $cm$ ?

A.

$3\,cm$ và $6\,cm$
B.

$6\,cm$ và $9\,cm$
C.

$6\,cm$ và $3\,cm$
D.

$9\,cm$ và $6\,cm$

Đáp án : C

Phương pháp giải :

Từ kiến thức lý thuyết về hình hộp chữ nhật kết hợp với tính chất của hình chữ nhật để giải bài toán và chọn đáp án đúng.

Lời giải chi tiết :

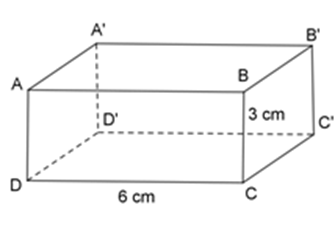
Vì $ABC{\rm{D}}.A'B'C'D'$ là hình hộp chữ nhật nên $ABCD,$ $ABB'A'$ là hình chữ nhật.

Xét hình chữ nhật $ABCD$ có: $AD = BC = 3cm,DC = AB = 6cm$

Xét hình chữ nhật $ABB'A'$ có: $A'B' = AB = 6\;cm$

Vậy $A'B'$ và $AD$ lần lượt dài $6 cm$ và $3 cm.$

Câu 4 :

A.

$30{m^3}$
B.

$22,5{m^3}$
C.

$7,5{m^3}$
D.

$5,7{m^3}$

Đáp án : C

Phương pháp giải :

Áp dụng công thức tính thể tích hình hộp chữ nhật $V=abc$ (với $a,b,c$ là chiều dài, chiều rộng, chiều cao) để giải bài toán.

Lời giải chi tiết :

Vì bể nước có dạng hình hộp chữ nhật nên ta tính được thể tích bể nước là: $V = 4.3.2,5 = 30\;{m^3}$

Vì $\dfrac{3}{4}$bể đang chứa nước nên thể tích phần bể chứa nước là: Vchứa nước$ = \dfrac{3}{4}V = \dfrac{3}{4}30 = 22,5\;{m^3}$

Vậy thể tích phần bể không chứa nước là: Vkhông chứa nước = V $ - $ Vchứa nước$ = 30 - 22,5 = 7,5\;{m^3}$

Câu 5 :

A.

$\dfrac{2}{9}$
B.

$\dfrac{{27}}{8}$
C.

$\dfrac{8}{{27}}$
D.

$\dfrac{4}{9}$

Đáp án : C

Phương pháp giải :

- Áp dụng công thức tính thể tính hình lập phương $V=a^3$ (với $a$ là độ dài một cạnh hình lập phương) để giải bài toán.

Lời giải chi tiết :

Gọi chiều dài một cạnh của hình lập phương $A$ là $a$ .

Vì hình lập phương $A$ có cạnh bằng $\dfrac{2}{3}$ cạnh của hình lập phương $B$ nên chiều dài $1$ cạnh của hình lập phương $B$ là $\dfrac{3}{2}a$.

Thể tích hình lập phương A là: ${V_A} = {a^3}$

Thể tích hình lập phương B là: ${V_B} = {\left( {\dfrac{3}{2}a} \right)^3} = \dfrac{{27}}{8}{a^3}$

$ \Rightarrow {V_B} = \dfrac{{27}}{8}{V_A} \Rightarrow {V_A} = \dfrac{8}{{27}}{V_B}$

Vậy thể tích hình lập phương $A$ bằng $\dfrac{8}{{27}}$ thể tích hình lập phương $B$ .

Câu 6 :

A.

$1782\,c{m^3}$
B.

$1728\,c{m^3}$
C.

$144\,c{m^2}$
D.

$1827\,c{m^3}$

Đáp án : B

Phương pháp giải :

+ Từ các điều kiện đề bài tìm cạnh của hình lập phương.

+ Sử dụng công thức thể tích hình lập phương để tính toán.

Lời giải chi tiết :

Chiếc hộp hình lập phương không nắp gồm $5$ hình vuông, mỗi hình vuông được sơn $2$ mặt nên diện tích mỗi hình vuông là: $1440:10 = 144\left( {c{m^2}} \right)$

Vì diện tích hình vuông bằng bình phương một cạnh nên cạnh của hình lập phương bằng $12 cm$ nên thể tích của hình lập phương bằng ${12^3} = 1728\left( {c{m^3}} \right)$ .

Câu 7 :

A.

$86000$ đồng
B.

$69000$ đồng
C.

$96600$ đồng
D.

$96000$ đồng

Đáp án : D

Phương pháp giải :

- Áp dụng công thức tính diện tích hình vuông và kiến thức lý thuyết về hình lập phương để giải bài toán.

Lời giải chi tiết :

Thùng sắt (không nắp) có dạng hình lập phương $ \Rightarrow $Thùng sắt có 5 mặt bằng nhau.

Diện tích một mặt thùng sắt là:

$S = 0,{8^2} = 0,64\;{m^2}$

Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là:

${S_{mt}} = {S_{mn}} = 5S = 5.0,64 = 3,2\;{m^2}$

Số tiền người thuê sơn thùng sắt cần trả là:

$({S_{mt}} + {S_{mn}}).15000 = (3,2 + 3,2).15000 = 6,4.15000 = 96000$ đồng.

Câu 8 :

A.

64,42 m²
B.

47,32 m²
C.

48,92 m²
D.

53,12 m²

Đáp án : A

Phương pháp giải :

Ta đi tính diện tích xung quanh ${S_2}$, diện tích trần ${S_1}$.

Từ đó, diện tích cần quét vôi là $S = \left( {{S_1} + {S_2}} \right) - 5,80$.

Lời giải chi tiết :

Diện tích trần nhà là: S₁ = 4,5 . 3,8 = 17,1 (m²)

Diện tích của bốn bức tường là: S₂ = 2. (4,5 + 3,8) . 3,2 = 53,12 (m²)

Từ đó, diện tích cần quét vôi là: $S = \left( {{S_1} + {S_2}} \right) - 5,80$= 17,1 + 53,12 – 5,8 = 64,42 (m²)

Vậy diện tích cần quét vôi là 64,42 (m²)

Câu 9 :

Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Diện tích các mặt $ABCD,\,\,BCC'B'$và $DCC'D'$lần lượt là $108c{m^2},72c{m^2}$và $96c{m^2}$. Tính thể tích của hình hộp

A.

276 cm³
B.

864 cm³
C.

864 cm²
D.

276 cm²

Đáp án : B

Phương pháp giải :

Gọi độ dài các cạnh $AB,\,\,BC,\,\,CC'$ lần lượt là $a,\,\,b,{\rm{ }}c\left( {a,\,\,b,{\rm{ }}c > 0;\,\,cm} \right)$

Diện tích các mặt đã cho là tích của hai kích thước. Thể tích của hình hộp là tích của ba kích thước. Vì vậy ta cần sử dụng cáctích của từng cặp hai kích thước để đưa về tích của ba kích thước.

Lời giải chi tiết :

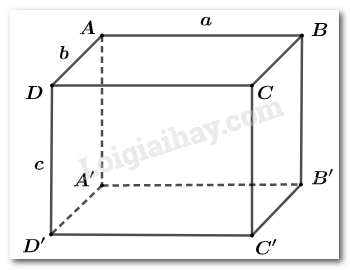
Gọi độ dài các cạnh $AB,\,\,BC,\,\,CC'$ lần lượt là $a,\,\,b,{\rm{ }}c\,\,\left( {a,\,\,b,{\rm{ }}c > 0;\,\,cm} \right)$

a) Theo đề bài, ta có:

$\left. \begin{array}{l}ab = 108\,\,\left( {c{m^2}} \right)\\bc = 72\,\,\left( {c{m^2}} \right)\\ca = 96\,\,\left( {c{m^2}} \right)\end{array} \right\} \Rightarrow ab.bc.ca = 108.72.96$

$ \Rightarrow {\left( {abc} \right)^2} = 746496$$ \Rightarrow abc = 864\,\left( {c{m^3}} \right)$$ \Rightarrow V = abc = 864\,\,\left( {c{m^3}} \right)$

Câu 10 :

Hình hộp chữ nhật với ba kích thước lần lượt là a, 2a, 4a thì có thể tích là

A.

a³ ( đvtt)
B.

2a³ ( đvtt)
C.

8a³ ( đvtt)
D.

8a² ( đvdt)

Đáp án : C

Phương pháp giải :

Thể tích hình hộp chữ nhật: V = chiều dài . chiều rộng . chiều cao

Lời giải chi tiết :

V = a. 2a. 4a = 8a³ ( đvtt)

Câu 11 :

A.

$216c{m^3}$
B.

$81c{m^3}$
C.

288 cm³
D.

96 cm³

Đáp án : D

Phương pháp giải :

Tính độ dài chiều rộng và chiều cao của hình hộp

Thể tích hình hộp chữ nhật: V = chiều dài . chiều rộng . chiều cao

Lời giải chi tiết :

Chiều rộng của hình hộp chữ nhật là: $6.\frac{1}{3} = 2\,\left( {cm} \right)$

Chiều cao của hình hộp chữ nhật là: 4 . 2 = 8 ( cm)

Thể tích của hình hộp chữ nhật là: 6 . 2 . 8 = 96 ( cm³)

Câu 12 :

Cho hình lập phương $ABC{\rm{D}}.A'B'C'D'$ có độ dài cạnh hình lập phương là 4 cm. Hỏi thể tích hình lập phương là bao nhiêu?

A.

16 cm³
B.

4 cm³
C.

32 cm³
D.

64 cm³

Đáp án : D

Phương pháp giải :

Thể tích hình lập phương cạnh a là V = a³

Lời giải chi tiết :

Thể tích hình lập phương đó là:

V = 4³ = 64 (cm³)

Câu 13 :

A.

40 cm
B.

30 cm
C.

60 cm
D.

50 cm

Đáp án : B

Phương pháp giải :

Tính thể tích nước ban đầu

Tính thể tích phần bể chứa nước lúc sau

Tính chiều cao mực nước lúc sau

Lời giải chi tiết :

Thể tích phần bể chứa nước ban đầu là:

$V = 80.50.25 = 100000\;c{m^3}$

Sau khi cho vào một hòn đá thể tích tăng 20000 cm³. Vậy thể tích phần bể chứa nước lúc sau là:

${V_1} = V + 20000 = 100000 + 20000 = 120000\;c{m^3}$

Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi.

Gọi chiều cao mực nước lúc sau là h cm. Ta có:

$V = 80.50.h = 120000 \Rightarrow h = \frac{V}{{80.50}} = \frac{{120000}}{{80.50}} = 30\;cm$

Câu 14 :

A.

96 000 đồng
B.

61 440 đồng
C.

102 400 đồng
D.

122 880 đồng

Đáp án : C

Phương pháp giải :

Tính diện tích phần cần sơn

Tính tiền = diện tích cần sơn . giá tiền

Lời giải chi tiết :

Thùng sắt (không nắp) có dạng hình lập phương.$ \Rightarrow $Thùng sắt có 5 mặt bằng nhau.

Diện tích một mặt thùng sắt là:

$S = 0,{8^2} = 0,64\;{m^2}$

Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là:

${S_{mt}} = {S_{mn}} = 5S = 5.0,64 = 3,2\;{m^2}$

Số tiền người thuê sơn thùng sắt cần trả là:

$({S_{mt}} + {S_{mn}}).16000 = (3,2 + 3,2).16000 = 6,4.16000 = 102400$( đồng)

Trắc nghiệm Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 4: Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Trắc nghiệm Bài 1: Hình hộp chữ nhật - Hình lập phương Toán 7 Chân trời sáng tạo

Luyện tập và củng cố kiến thức Bài 1: Hình hộp chữ nhật - Hình lập phương Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết

Xem chi tiết

Bài giải mới nhất

Trắc nghiệm Bài 2: Diện tích xung quanh và thể tích của hình hộp chữ nhật - Hình lập phương Toán 7 Chân trời sáng tạo

Báo lỗi góp ý