-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Các hình khối trong thực tiễn
-
Chương 4: Góc và đường thẳng song song
-
Chương 5: Một số yếu tố thống kê
-
Chương 6: Các đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số
-
Chương 8: Tam giác
- Bài 1: Góc và cạnh của một tam giác
- Bài 2: Tam giác bằng nhau
- Bài 3: Tam giác cân
- Bài 4: Đường vuông góc và đường xiên
- Bài 5: Đường trung trực của một đoạn thẳng
- Bài 6: Tính chất ba đường trung trực của tam giác
- Bài 7: Tính chất ba đường trung tuyến của tam giác
- Bài 8: Tính chất ba đường cao của tam giác
- Bài 9: Tính chất ba đường phân giác của tam giác
-
Chương 9: Một số yếu tố xác suất
Trắc nghiệm Bài 4: Định lí và chứng minh một định lí Toán 7 Chân trời sáng tạo
Đề bài
Chọn câu đúng.
-
A.
Giả thiết của định lý là điều cho biết.
-
B.
Kết luận của định lý là điều được suy ra.
-
C.
Giả thiết của định lý là điều được suy ra.
-
D.
Cả A, B đều đúng.
Định lý sau được phát biểu thành lời là:
-
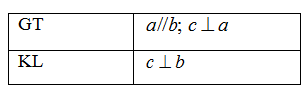
A.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
-
B.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
-
C.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
-
D.
Cả A, B, C đều sai.
Phát biểu định lý sau bằng lời:
-
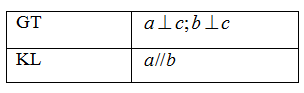
A.
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
-
B.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
-
C.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
-
D.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
-
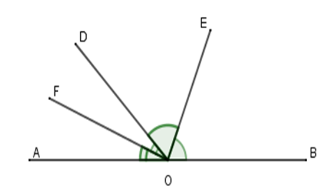
A.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
-
B.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
-
C.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
-
D.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
-
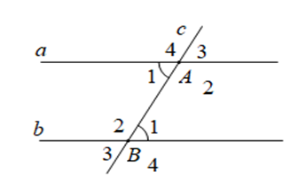
A.
\(a//b;\,a \bot c\)
-
B.
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
-
C.
\(a//b;\,a//c\)
-
D.
\(a//b,\) \(c\) bất kì.
Trong các câu sau, câu nào cho một định lí
-
A.
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
-
B.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
-
C.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
-
D.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Chứng minh định lý là
-
A.
Dùng lập luận để từ giả thiết suy ra kết luận
-
B.
Dùng hình vẽ để từ giả thiết suy ra kết luận
-
C.
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
-
D.
Cả A, B, C đều sai
Chứng minh định lý là
-
A.
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
-
B.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
-
C.
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
-
D.
Cả A, B, C đều sai.
Trong các câu sau, câu nào không cho một định lí:
-
A.
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
-
B.
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
-
C.
Hai góc đối đỉnh thì bằng nhau.
-
D.
Hai góc kề nhau thì có tổng số đo là 180 độ
Chọn câu sai:
-
A.
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
-
B.
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
-
C.
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
-
D.
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Lời giải và đáp án
Chọn câu đúng.
-
A.
Giả thiết của định lý là điều cho biết.
-
B.
Kết luận của định lý là điều được suy ra.
-
C.
Giả thiết của định lý là điều được suy ra.
-
D.
Cả A, B đều đúng.
Đáp án : D
Sử dụng lý thuyết về định lý.
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý sau được phát biểu thành lời là:
-
A.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
-
B.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.
-
C.
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc \(60^\circ .\)
-
D.
Cả A, B, C đều sai.
Đáp án : A
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra.
Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Phát biểu định lý sau bằng lời:
-
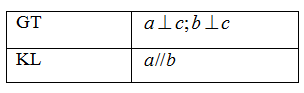
A.
Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau.
-
B.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau.
-
C.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
-
D.
Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.
Đáp án : C
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau.
Cho định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
-
A.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
-
B.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOF\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OA\)
-
C.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOE\).
Kết luận: \(OE \bot OF\)
-
D.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OB \bot OF\)
Đáp án : A
Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Giả thiết: Cho góc bẹt \(AOB\) và tia \(OD.\) \(OE\) là phân giác góc \(BOD\); \(OF\) là phân giác góc \(AOD\).
Kết luận: \(OE \bot OF\)
Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là
-
A.
\(a//b;\,a \bot c\)
-
B.
\(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
-
C.
\(a//b;\,a//c\)
-
D.
\(a//b,\) \(c\) bất kì.
Đáp án : B
Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra
Giả thiết của định lý trên là \(a//b,\) \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\)
Trong các câu sau, câu nào cho một định lí
-
A.
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
-
B.
Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
-
C.
Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
-
D.
Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Đáp án : A
Sử dụng lý thuyết về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Chứng minh định lý là
-
A.
Dùng lập luận để từ giả thiết suy ra kết luận
-
B.
Dùng hình vẽ để từ giả thiết suy ra kết luận
-
C.
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
-
D.
Cả A, B, C đều sai
Đáp án : A
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Chứng minh định lý là
-
A.
Dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
-
B.
Dùng hình vẽ và các khẳng định đã biết để từ giả thiết suy ra kết luận
-
C.
Dùng đo đạc thực tế để từ giả thiết suy ra kết luận.
-
D.
Cả A, B, C đều sai.
Đáp án : A
Sử dụng định nghĩa “chứng minh định lý”.
Chứng minh định lý là dùng lập luận để từ giả thiết và các khẳng định đúng đã biết suy ra kết luận.
Trong các câu sau, câu nào không cho một định lí:
-
A.
Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
-
B.
Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.
-
C.
Hai góc đối đỉnh thì bằng nhau.
-
D.
Hai góc kề nhau thì có tổng số đo là 180 độ
Đáp án : D
Sử dụng nhận xét về định lý: Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí.
+ “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
+ “Nếu một đường thẳng cắt 2 đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau.”
+ “Hai góc đối đỉnh thì bằng nhau”
Câu D không là định lí vì khẳng định D sai
Chọn câu sai:
-
A.
Định lí thường được phát biểu ở dạng: “ Vì … nên….”
-
B.
Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
-
C.
Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra 1 phản ví dụ
-
D.
Để chỉ ra một khẳng định là đúng, ta đi chứng minh.
Đáp án : A
Lý thuyết về định lí
Khẳng định A sai vì định lí thường được phát biểu ở dạng: “ Nếu … thì …”
Các khẳng định B,C,D đúng .
Luyện tập và củng cố kiến thức Bài 3: Hai đường thẳng song song Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tia phân giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Các góc ở vị trí đặc biệt Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 3: Đại lượng tỉ lệ nghịch Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Đại lượng tỉ lệ thuận Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Làm quen với xác suất của biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Làm quen với biến cố ngẫu nhiên Toán 7 Chân trời sáng tạo
