Trả lời câu hỏi 3 Bài 4 trang 18 SGK Toán 7 Tập 2
Kết quả kiểm tra của lớp 7A (với cùng đề kiểm tra của lớp 7C) được cho qua bảng “tần số”...
Đề bài
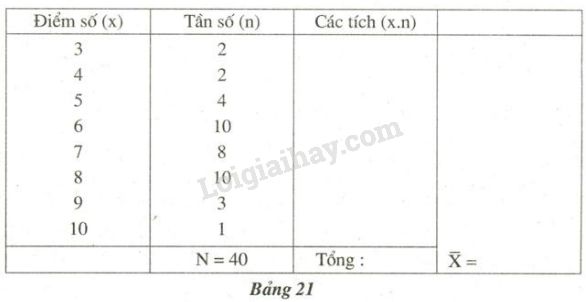
Kết quả kiểm tra của lớp \(7A\) (với cùng đề kiểm tra của lớp \(7C\)) được cho qua bảng “tần số” sau đây. Hãy dùng công thức trên để tính điểm trung bình của lớp \(7A\) (bảng 21):
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Số trung bình cộng của một dấu hiệu được tính từ bảng tần số theo cách sau:
- Nhân từng giá trị với tần số tương ứng.
- Cộng tất cả các tích vừa tìm được.
- Chia tổng đó cho các giá trị (tức tổng các tần số).
Ta có công thức:
\(\overline{X} = \dfrac{x_{1}n_{1}+ x_{2}n_{2}+ x_{3}n_{3}+ ... + x_{k}n_{k}}{N}\)
Trong đó:
\({x_1},{\text{ }}{x_2},{\text{ }} \ldots ,{\text{ }}{x_k}\) là \(k\) giá trị khác nhau của dấu hiệu \(X\).
\({n_1},{\text{ }}{n_2},{\text{ }} \ldots ,{\text{ }}{n_k}\) là tần số tương ứng.
\(N\) là số các giá trị.
\(\overline{X}\) là số trung bình của dấu hiệu \(X\).
Lời giải chi tiết
|
Điểm số (\(x\)) |
Tần số (\(n\)) |
Các tích (\(x.n\)) |
|
|
\(3\) |
\(2\) |
\(6\) |
|
|
\(4\) |
\(2\) |
\(8\) |
|
|
\(5\) |
\(4\) |
\(20\) |
|
|
\(6\) |
\(10\) |
\(60\) |
|
|
\(7\) |
\(8\) |
\(56\) |
|
|
\(8\) |
\(10\) |
\(80\) |
|
|
\(9\) |
\(3\) |
\(27\) |
|
|
\(10\) |
\(1\) |
\(10\) |
|
|
\(N = 40\) |
Tổng: \(267\) |
\(\overline X = \dfrac{{267}}{{40}} \)\(\,= 6,675\) |
|
Bình luận
Chia sẻ
- Trả lời câu hỏi 4 Bài 4 trang 19 SGK Toán 7 Tập 2
- Bài 14 trang 20 SGK Toán 7 tập 2
- Bài 15 trang 20 SGK Toán 7 tập 2
- Bài 16 trang 20 SGK Toán 7 tập 2
- Bài 17 trang 20 SGK Toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
