Bài 17 trang 20 SGK Toán 7 tập 2
Đề bài
Theo dõi thời gian làm một bài toán (tính bằng phút) của \(50\) học sinh, thầy giáo lập được bảng \(25\):
a) Tính số trung bình cộng.
b) Tìm mốt của dấu hiệu.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tìm số trung bình cộng theo công thức:
\(\overline{X} = \dfrac{x_{1}n_{1}+ x_{2}n_{2}+ x_{3}n_{3}+ ... + x_{k}n_{k}}{N}\)
Trong đó:
\({x_1},{\text{ }}{x_2},{\text{ }} \ldots ,{\text{ }}{x_k}\) là \(k\) giá trị khác nhau của dấu hiệu \(X\).
\({n_1},{\text{ }}{n_2},{\text{ }} \ldots ,{\text{ }}{n_k}\) là tần số tương ứng.
\(N\) là số các giá trị.
\(\overline{X}\) là số trung bình của dấu hiệu \(X\).
- Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số. Kí hiệu là \(M_o\).
Lời giải chi tiết
a) Số trung bình cộng về thời gian làm một bài toán của \(50\) học sinh là:
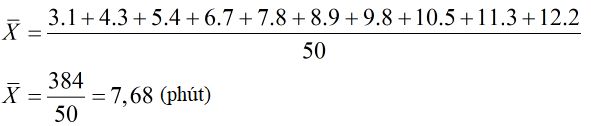
b) Tần số lớn nhất là \(9\), giá trị có tần số \(9\) là \(8\).
Vậy mốt của dấu hiệu: \({M_o} = 8\)
Bình luận
Chia sẻ
- Bài 18 trang 21 SGK Toán 7 tập 2
- Bài 19 trang 22 SGK Toán 7 tập 2
- Đề kiểm tra 15 phút - Đề số 1 – Bài 3,4 - Chương 3 – Đại số 7
- Đề kiểm tra 15 phút - Đề số 2 – Bài 3,4 - Chương 3 – Đại số 7
- Đề kiểm tra 15 phút - Đề số 3 – Bài 3,4 - Chương 3 – Đại số 7
>> Xem thêm
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 7 trên Tuyensinh247.com cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
