Lý thuyết hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác mà ba cạnh của tam giác này bằng ba cạnh của tam giác kia và ba góc đối diện với ba cạnh ấy của tam giác này bằng ba góc đối diện với b a cạnh của tam giác kia.
1. Các kiến thức cần nhớ
Hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
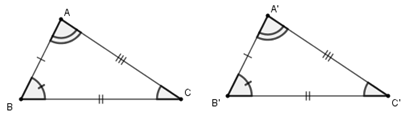
Để kí hiệu sự bằng nhau của tam giác \(ABC\) và tam giác \(A'B'C'\) ta viết:
\(∆ABC= ∆A'B'C'.\)
Ví dụ:
\(\Delta ABC = \Delta A'B'C'\) \( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat A'\\\widehat B = \widehat B'\\\widehat C = \widehat C'\\AB = A'B'\\AC = A'C'\\BC = B'C'\end{array} \right.\)
Trong đó \(A,\,A'\) là hai đỉnh tương ứng, \(AB,\,A'B'\) là hai cạnh tương ứng, \(\widehat A,\widehat {A'}\) là hai góc tương ứng.
Lưu ý
Khi kí hiệu sự bằng nhau của hai tam giác, các chữ cái chỉ tên các đỉnh tương ứng được viết theo cùng thứ tự
2. Một số dạng toán thường gặp
Dạng 1: Từ hai tam giác bằng nhau, xác định các cạnh bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc.
Phương pháp:
Căn cứ vào các đỉnh tương ứng của hai tam giác bằng nhau để xác định các yếu tố cần thiết.
Dạng 2: Viết các cặp tam giác bằng nhau khi cho các cặp góc, cặp cạnh bằng nhau
Phương pháp: Dựa vào các cặp góc, các cặp cạnh bằng nhau ta viết các cặp tam giác bằng nhau theo đúng thứ tự các đỉnh tương ứng.
Bình luận
Chia sẻ
- Trả lời câu hỏi 1 Bài 2 trang 110 SGK Toán 7 Tập 1
- Trả lời câu hỏi 2 Bài 2 trang 111 SGK Toán 7 Tập 1
- Trả lời câu hỏi 3 Bài 2 trang 111 SGK Toán 7 Tập 1
- Bài 10 trang 111 SGK Toán 7 tập 1
- Bài 11 trang 112 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
