Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Chân trời sáng tạo

1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác

1. Đường tròn ngoại tiếp tam giác

Định nghĩa đường tròn ngoại tiếp tam giác

– Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn.

– Đường tròn ngoại tiếp tam giác có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác.

Ví dụ:

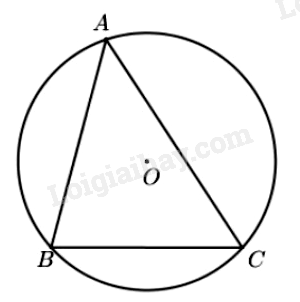
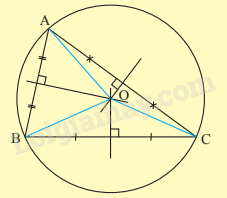
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).

- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.

Đường tròn ngoại tiếp tam giác đều

Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).

Ví dụ:

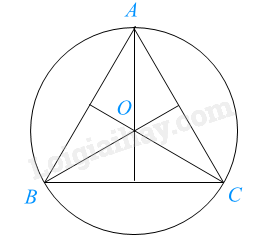
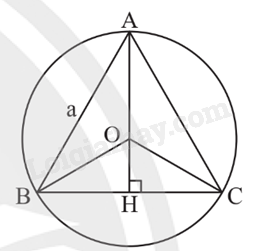
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).

Đường tròn ngoại tiếp tam giác vuông

Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.

Ví dụ:

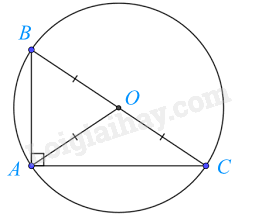
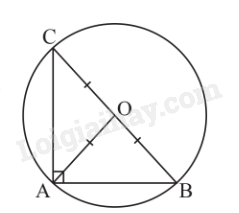
Tam giác ABC nội tiếp đường tròn (O; BO).

2. Đường tròn nội tiếp một tam giác

Định nghĩa đường tròn nội tiếp tam giác

- Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, khi đó tam giác được gọi là tam giác ngoại tiếp đường tròn.

- Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kinh bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.

Ví dụ:

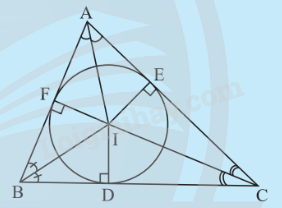
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).

- Tâm I là giao điểm của ba đường phân giác của tam giác.

Đường tròn nội tiếp tam giác đều

Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).

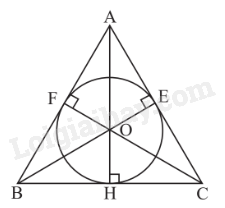
Ví dụ:

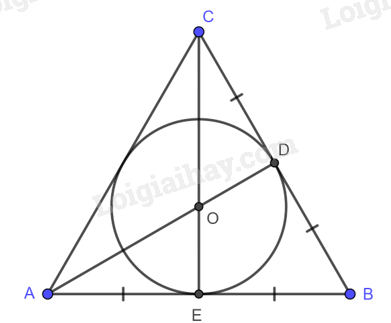
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 65, 66, 67 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1). a) So sánh độ dài của đoạn thẳng OA, OB và OC. b) Vẽ đường tròn đi qua ba điểm A, B, C.
Giải mục 2 trang 67, 68, 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7). a) Chứng minh rằng IE = IF = ID. b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
Giải bài tập 1 trang 68 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác đều ABC có cạnh bằng 6 cm. a) Nêu các vẽ đường tròn ngoại tiếp tam giác ABC. b) Nêu các vẽ đường tròn nội tiếp tam giác ABC. c) Tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB). a) Chứng minh OI vuông góc với BC. b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).
Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). a) Chứng minh 2AD = AB + AC – BC. b) Tìm các hệ thức tương tự như ở câu a.
Giải bài tập 4 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm.
Giải bài tập 5 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác.