Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo

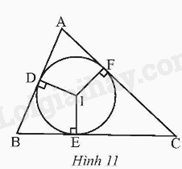
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). a) Chứng minh 2AD = AB + AC – BC. b) Tìm các hệ thức tương tự như ở câu a.

Đề bài

Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).

a) Chứng minh 2AD = AB + AC – BC.

b) Tìm các hệ thức tương tự như ở câu a.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra AD = AF; BD = BE; FC = EC rồi thay vào hệ thức 2AD = AB + AC – BC để chứng minh.

Lời giải chi tiết

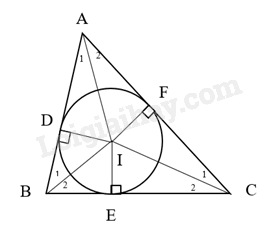
a) Ta có D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC nên tính chất hai tiếp tuyến bằng nhau, ta có:

\(AD = AE; CF = CE; BD = BE\) (1)

Ta có:

\(AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC) \)

\(= AD + BD + AF + FC – BE - EC\) (2)

Từ (1) và (2) suy ra

\(AB + AC – BC = AD + BE + AD + EC – BE – EC\)

\(= (AD + AD) + (BE - BE) + (CE - CE) = 2AD\)

b) Các hệ thức tương tự như ở câu a:

\(2AF = AB + AC – BC\);

\(2BD = 2BE = AB + BC – AC\);

\(2EC = 2FC = AC + BC – AB\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 4 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Tính diện tích tam giác đều có bán kính đường tròn nội tiếp bằng 1 cm.
Giải bài tập 5 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Một trại nuôi gia súc có dạng hình tam giác đều cạnh 100 m (Hình 12). Người ta muốn đặt một trụ đèn cao áp tại một điểm cách đều ba đỉnh của tam giác. Nêu cách xác định vị trí đặt đèn và tính khoảng cách từ điểm đó đến ba đỉnh của tam giác.
Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB). a) Chứng minh OI vuông góc với BC. b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).
Giải bài tập 1 trang 68 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tam giác đều ABC có cạnh bằng 6 cm. a) Nêu các vẽ đường tròn ngoại tiếp tam giác ABC. b) Nêu các vẽ đường tròn nội tiếp tam giác ABC. c) Tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Giải mục 2 trang 67, 68, 69 SGK Toán 9 tập 2 - Chân trời sáng tạo
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7). a) Chứng minh rằng IE = IF = ID. b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
Giải mục 1 trang 65, 66, 67 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm của đường trung trực của đoạn thẳng AB và BC (Hình 1). a) So sánh độ dài của đoạn thẳng OA, OB và OC. b) Vẽ đường tròn đi qua ba điểm A, B, C.
Lý thuyết Đường tròn ngoại tiếp tam giác, đường tròn nội tiếp tam giác Toán 9 Chân trời sáng tạo
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác