Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống Bài 5. Dãy số Toán 11 kết nối tri thức

Lý thuyết Dãy số - SGK Toán 11 Kết nối tri thức


1. Định nghĩa dãy số

Tổng hợp đề thi giữa kì 1 lớp 11 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh

1. Định nghĩa dãy số

  • Dãy số vô hạn

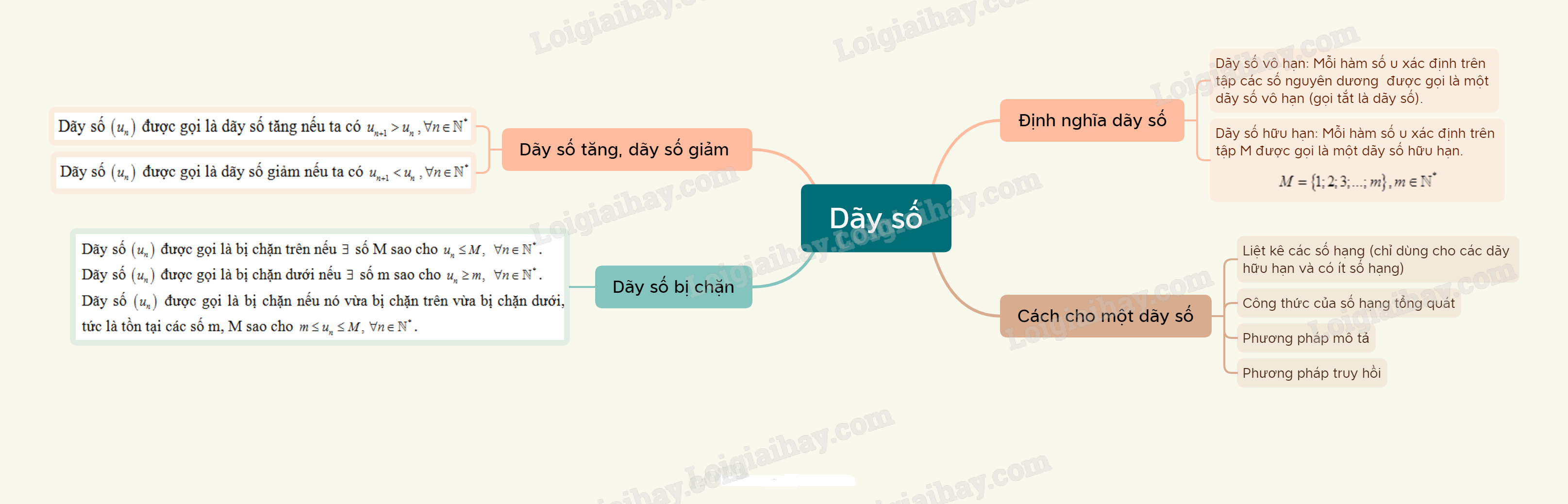
Mỗi hàm số u xác định trên tập các số nguyên dương \({\mathbb{N}^*}\) được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu là \(u = u\left( n \right)\).

Ta thường viết \({u_n}\) thay cho \(u\left( n \right)\) và kí hiệu dãy số \(u = u\left( n \right)\)bởi \(u\left( n \right)\), do đó dãy số \(\left( {{u_n}} \right)\)được viết dưới dạng khai triển \({u_1},{u_2},{u_3},...,{u_n},...\)

Số \({u_1}\) là số hạng đầu; \({u_n}\)là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

*Chú ý: Nếu \(\forall n \in {\mathbb{N}^*},{u_n} = c\)thì \(\left( {{u_n}} \right)\)được gọi là dãy số không đổi.

  • Dãy số hữu hạn

Mỗi hàm số u xác định trên tập \(M = \left\{ {1;2;3;...;m} \right\},m \in {\mathbb{N}^*}\) được gọi là một dãy số hữu hạn.

Dạng khai triển của dãy số hữu hạn là \({u_1},{u_2},{u_3},...,{u_m}\).

Số \({u_1}\) gọi là số hạng đầu, \({u_m}\)là số hạng cuối.

2. Cách cho một dãy số

Một dãy số có thể cho bằng:

  • Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).
  • Công thức của số hạng tổng quát.
  • Phương pháp mô tả.
  • Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm và dãy số bị chặn

  • Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có \({u_{n + 1}} > {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).

Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có \({u_{n + 1}} < {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).

  • Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu \(\exists \) số M sao cho \({u_n} \le M,\) \(\forall n \in {\mathbb{N}^*}\).

Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu \(\exists \) số m sao cho \({u_n} \ge m,\) \(\forall n \in {\mathbb{N}^*}\).

Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho \(m \le {u_n} \le M,\)\(\forall n \in {\mathbb{N}^*}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 1 trang 42, 43 SGK Toán 11 tập 1 - Kết nối tri thức

    Viết năm số chính phương đầu theo thứ tự tăng dần. Từ đó, dự đoán công thức tính số chính phương thứ n.

  • Giải mục 2 trang 43, 44 SGK Toán 11 tập 1 - Kết nối tri thức

    Xét dãy số (({u_n})) gồm tất cả các số nguyên dương chia hết cho 5: (5;10;15;20;25;30; ldots ) a) Viết công thức số hạng tổng quát ({u_n}) của dãy số b) Xác định số hạng đầu và viết công thức tính số hạng thứ n theo số hạng thứ n – 1 của dãy số. Công thức thu được gọi là hệ thức truy hồi

  • Giải mục 3 trang 45, 46 SGK Toán 11 tập 1 - Kết nối tri thức

    a) Xét dãy số (left( {{u_n}} right)) với ({u_n} = 3n - 1). Tính ({u_{n + 1}}) và so sánh với ({u_n}) b) Xét dãy số (left( {{v_n}} right)) với ({v_n} = frac{1}{{{n^2}}}). Tính ({v_{n + 1}}) Và so sánh với ({v_n})

  • Bài 2.1 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức

    Viết năm số hạng đầu và số hạng thứ 100 của các dãy số (left( {{u_n}} right)) có số hạng tổng quát cho bởi: a) ({u_n} = 3n - 2) b) ({u_n} = {3.2^n}) c) ({u_n} = {left( {1 + frac{1}{n}} right)^n})

  • Bài 2.2 trang 46 SGK Toán 11 tập 1 - Kết nối tri thức

    Dãy số (left( {{u_n}} right))cho bởi hệ thức truy hồi: ({u_1} = 1,;;;{u_n} = n.{u_{n - 1}}) với (n ge 2) a) Viết năm số hạng đầu của dãy số. b) Dự đoán công thức số hạng tổng quát ({u_n}).

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store