Copyright © 2021 loigiaihay.com
CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ
Bài 1. Đơn thức và đa thức nhiều biến
Bài 2. Các phép toán với đa thức nhiều biến
Bài 3. Hằng đẳng thức đáng nhớ
Bài 4. Phân tích đa thức thành nhân tử
Bài 5. Phân thức đại số
Bài 6. Cộng, trừ phân thức
Bài 7. Nhân, chia phân thức
Bài tập cuối chương 1
CHƯƠNG 2. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình chóp tam giác đều - Hình chóp tứ giác đều
Bài 2. Diện tích xung quanh và thể tích của hình chóp tam giác đều - hình chóp tứ giác đều
Bài tập cuối chương 2
CHƯƠNG 3. ĐỊNH LÍ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP
Bài 1. Định lí Pythagore
Bài 2. Tứ giác
Bài 3. Hình thang - Hình thang cân
Bài 4. Hình bình hành - Hình thoi
Bài 5. Hình chữ nhật - Hình vuông
Bài tập cuối chương 3
CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Thu thập và phân loại dữ liệu
Bài 2. Lựa chọn dạng biểu đồ để biểu diễn dữ liệu
Bài 3. Phân tích dữ liệu
Bài tập cuối chương 4
CHƯƠNG 5. HÀM SỐ VÀ ĐỒ THỊ
Bài 1. Khái niệm hàm số
Bài 2. Tọa độ của một điểm và đồ thị của hàm số
Bài 3. Hàm số bậc nhất y=ax+b(a≠0)
Bài 4. Hệ số góc của đường thẳng
Bài tập cuối chương 5
CHƯƠNG 6. PHƯƠNG TRÌNH
Bài 1. Phương trình bậc nhất một ẩn
Bài 2. Giải bài toán bằng cách lập phương trình bậc nhất một ẩn
Bài tập cuối chương 6
CHƯƠNG 7. ĐỊNH LÍ THALES
Bài 1. Định lí Thalès trong tam giác
Bài 2. Đường trung bình của tam giác
Bài 3. Tính chất đường phân giác của tam giác
Bài tập cuối chương 7
CHƯƠNG 8. HÌNH ĐỒNG DẠNG
Bài 1. Hai tam giác đồng dạng
Bài 2. Các trường hợp đồng dạng của hai tam giác
Bài 3. Các trường hợp đồng dạng của hai tam giác vuông
Bài 4. Hai hình đồng dạng
Bài tập cuối chương 8
CHƯƠNG 9. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Mô tả xác suất bằng tỉ số
Bài 2. Xác suất lí thuyết và xác suất thực nghiệm
Bài tập cuối chương 9
Trắc nghiệm Trường hợp hai cạnh góc vuông Toán 8 có đáp án
Trắc nghiệm Trường hợp hai cạnh góc vuông
18 câu hỏi
Trắc nghiệm
Câu 1 :
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Câu 2 :
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác kia
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai
-
A.
\(\Delta MNP \backsim \Delta DFE\)
-
B.
\(\Delta MNP \backsim \Delta DEF\)
-
C.
\(\Delta MNP = \Delta DFE\)
-
D.
Cả A, B, C đều sai
Câu 4 :
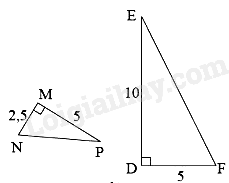
Cho tam giác ABC vuông tại A có: \(AB = 3cm,AC = 5cm\) và tam giác MNP vuông tại M có \(MN = 12cm,MP = 20cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
-
A.
\(\widehat B = \widehat D\)
-
B.
\(\widehat B = \frac{2}{3}\widehat D\)
-
C.
\(\frac{2}{3}\widehat B = \widehat D\)
-
D.
\(\widehat B = \frac{3}{4}\widehat D\)
-
A.
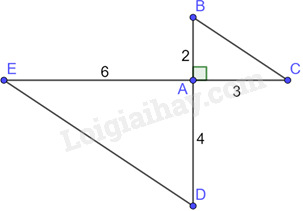
\(\widehat {ABC} + \widehat {EBD} = {80^0}\)
-
B.
\(\widehat {ABC} + \widehat {EBD} = {85^0}\)
-
C.
\(\widehat {ABC} + \widehat {EBD} = {95^0}\)
-
D.
\(\widehat {ABC} + \widehat {EBD} = {90^0}\)
-
A.
\(\widehat {BAH} = \widehat C\)
-
B.
\(\widehat {BAH} = \frac{2}{3}\widehat C\)
-
C.
\(\frac{2}{3}\widehat {BAH} = \widehat C\)
-
D.
Cả A, B, C đều sai
Câu 8 :
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{1}{2}.\) Gọi M, M’ lần lượt là trung điểm của BC và B’C’. Khi đó, tỉ số \(\frac{{AM}}{{A'M'}}\) bằng
-
A.
\(\frac{1}{3}\)
-
B.
\(\frac{1}{4}\)
-
C.
\(\frac{1}{2}\)
-
D.
\(2\)
Câu 9 :
Trên đoạn \(BC = 13cm,\) đặt đoạn \(BH = 4cm.\) Trên đường vuông góc với BC tại H, lấy điểm A sao cho \(HA = 6cm\)
Cho các khẳng định sau:
1. Số đo góc BAC bằng 80 độ
2. \(AB.AC = AH.BC\)
3. \(\widehat B > \widehat {CAH}\)
Có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
3
-
D.
2
Câu 10 :
Cho hình thang ABCD vuông tại A và D. Biết \(CD = 2AB = 2AD = 2a\) và \(BC = a\sqrt 2 .\) Gọi I là trung điểm của BC, H là chân đường vuông góc kẻ từ D xuống AC. Khi đó:
-
A.
\(\widehat {HDI} = {45^0}\)
-
B.
\(\widehat {HDI} = {40^0}\)
-
C.
\(\widehat {HDI} = {50^0}\)
-
D.
\(\widehat {HDI} = {55^0}\)
Câu 11 :
Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là đường thẳng AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D. Kẻ OM vuông góc với CD tại M. Khi đó:
-
A.
\(AC = \frac{4}{3}MC\)
-
B.
\(AC = \frac{3}{2}MC\)
-
C.
\(AC = \frac{2}{3}MC\)
-
D.
\(AC = MC\)
Câu 12 :
Cho tam giác ABC vuông tại A có M là trung điểm của BC. Gọi I là hình chiếu của M trên AC. Chọn đáp án đúng.
-
A.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{2}\)
-
B.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{3}\)
-
C.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{1}{4}\)
-
D.
\(\frac{{{S_{AIM}}}}{{{S_{ABC}}}} = \frac{2}{3}\)
-
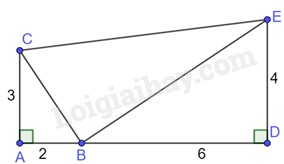
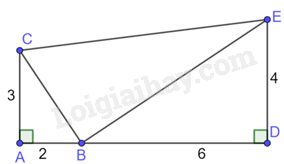
A.
\(CE = \sqrt {66} \)
-
B.
\(CE = \sqrt {65} \)
-
C.
\(CE = 8\)
-
D.
\(CE = 8,5\)
Câu 14 :
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’ có chu vi bằng 30cm, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}} = \frac{3}{2}\). Chu vi tam giác ABC là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
45cm
Câu 15 :
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{HC}}{{H'C'}}\). Biết rằng \(\widehat {A'B'C'} = \frac{1}{7}\widehat {BAC}.\) Chọn đáp án đúng
-
A.
\(\widehat {BAC} = {140^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Câu 16 :
Cho hình thang vuông ABCD, \(\left( {\widehat A = \widehat D = {{90}^0}} \right)\) có \(AB = 4cm,CD = 9cm\) và \(BC = 13cm.\) Khoảng cách từ M đến BC bằng:
-
A.
4cm
-
B.
5cm
-
C.
6cm
-
D.
7cm
Câu 17 :
Cho tam giác ABC vuông tại A, \(AC = 3AB = 3a.\) Lấy các điểm D, E thuộc AC sao cho \(AD = DE = EC.\) Khi đó,
-
A.
\(\widehat {AEB} + \widehat {ACB} = {40^0}\)
-
B.
\(\widehat {AEB} + \widehat {ACB} = {45^0}\)
-
C.
\(\widehat {AEB} + \widehat {ACB} = {50^0}\)
-
D.
\(\widehat {AEB} + \widehat {ACB} = {55^0}\)
Câu 18 :
Cho hình thang vuông ABCD \(\left( {\hat A = \hat D = {{90}^0}} \right)\) có AB = 4cm, CD = 9cm, BC = 13cm. Gọi M là trung điểm của AD. Tính \(\widehat {BMC}\) .
-
A.
\({60^0}\)
-
B.
\({110^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
