Giải mục 1 trang 74, 75 SGK Toán 11 tập 2 - Chân trời sáng tạo

a) Cho điểm (M) và đường thẳng (a) không đi qua (M). Trong mặt phẳng (left( {M,a} right))

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 1

a) Cho điểm \(M\) và đường thẳng \(a\) không đi qua \(M\). Trong mặt phẳng \(\left( {M,a} \right)\), dùng êke để tìm điểm \(H\) trên \(a\) sao cho \(MH \bot a\) (Hình 1a). Đo độ dài đoạn \(MH\).

b) Cho điểm \(M\) không nằm trên mặt phẳng sàn nhà \(\left( P \right)\). Dùng dây dọi để tìm hình chiếu vuông góc \(H\) của \(M\) trên \(\left( P \right)\) (Hình 1b). Đo độ dài đoạn \(MH\).

Phương pháp giải:

Thực hành đo đạc.

Lời giải chi tiết:

Thực hành đo đạc.

Thực hành 1

Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).

a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).

b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).

Phương pháp giải:

‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

‒ Cách tính khoảng cách từ một điểm đến một đường thẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên đường thẳng.

Lời giải chi tiết:

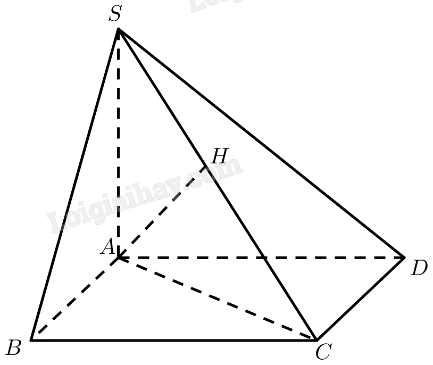
a) Ta có:

\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)

b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)

Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)

Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)

Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)

Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).

Vận dụng 1

Một quạt trần có bề dày của thân quạt là 20 cm. Người muốn treo quạt sao cho khoảng cách từ đỉnh quạt đến sàn nhà là 2,5 m. Hỏi phải làm cán quạt dài bao nhiêu? Cho biết trần nhà cao 3,6 m

Phương pháp giải:

Tính khoảng cách từ thân quạt đến trần nhà.

Lời giải chi tiết:

Đổi \(20cm = 0,2m\)

Độ dài của cán quạt là: \(3,6 - 2,5 - 0,2 = 0,9\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 76 SGK Toán 11 tập 2 - Chân trời sáng tạo
a) Cho đường thẳng (a) song song với mặt phẳng (left( P right)).
Giải mục 3 trang 77, 78 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho hai đường thẳng chéo nhau (a) và (b).
Giải mục 4 trang 78, 79, 80, 81 SGK Toán 11 tập 2 - Chân trời sáng tạo
Cho một khối hộp chữ nhật với các kích thước là (a,b,c)
Bài 1 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp (S.ABCD), đáy (ABCD) là hình thoi cạnh (a) có (O) là giao điểm của hai đường chéo
Bài 2 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hai tam giác cân (ABC) và (ABD) có đáy chung (AB) và không cùng nằm trong một mặt phẳng.
Bài 3 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp (S.ABCD) có đáy là hình vuông cạnh (a), (SA = SB = SC = SD = asqrt 2 ).
Bài 4 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình lăng trụ tam giác đều (ABC.A'B'C') có (AB = a), góc giữa hai mặt phẳng (left( {A'BC} right)) và (left( {ABC} right)) bằng ({60^ circ }).
Bài 5 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo
Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m
Bài 6 trang 82 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình hộp đứng (ABCD.A'B'C'D') có cạnh bên (AA' = 2a) và đáy (ABCD) là hình thoi có (AB = a) và (AC = asqrt 3 ).
Bài 7 trang 82 SGK Toán 11 tập 2 – Chân trời sáng tạo
Cho hình chóp tứ giác đều (S.ABCD) có tất cả các cạnh đều bằng (a) và có (O) là giao điểm hai đường chéo của đáy.
Bài 8 trang 82 SGK Toán 11 tập 2 – Chân trời sáng tạo
Tính thể tích của khối chóp cụt lục giác đều (ABCDEF.{rm{ }}A'B'C'D'E'F') với (O) và (O') là tâm hai đáy
Lý thuyết Khoảng cách trong không gian - Toán 11 Chân trời sáng tạo
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng