-
Toán 11 tập 1 - Chân trời sáng tạo
-
Giải Toán 11 tập 2 - Chân trời sáng tạo
Giải mục 1 trang 52, 53 SGK Toán 11 tập 1 - Chân trời sáng tạo
Tìm điểm giống nhau của các dãy số sau:
Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh
Hoạt động 1
Tìm điểm giống nhau của các dãy số sau:
a) 2; 5; 8; 11; 14 (xem Hình 1).
b) 2; 4; 6; 8.
c) 5; 10; 15; 20; 25.
d) ‒5; ‒2; 1; 4; 7; 10.
Phương pháp giải:
Xem hai số hạng liên tiếp của dãy có liên hệ gì.
Lời giải chi tiết:
Ta thấy:
a) Số sau hơn số liền trước 3 đơn vị.
b) Số sau hơn số liền trước 2 đơn vị.
c) Số sau hơn số liền trước 5 đơn vị.
d) Số sau hơn số liền trước 3 đơn vị.
Điểm giống nhau của các dãy số này là hai số hạng liền nhau hơn kém nhau một số không đổi.
Thực hành 1
Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.
a) 3; 7; 11; 15; 19; 23.
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).
c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.
Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
a) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai \(d = 4\).
b) Ta có: \({u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = 9\).
c) Ta có: \({v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a\).
Vậy dãy số \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = a\).
Thực hành 2
Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.
Phương pháp giải:
Dựa vào tính chất:
‒ Tam giác vuông có một góc bằng \({90^ \circ }\).
‒ Tổng ba góc trong tam giác bằng \({180^ \circ }\).
Lời giải chi tiết:
Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).
Vận dụng 1
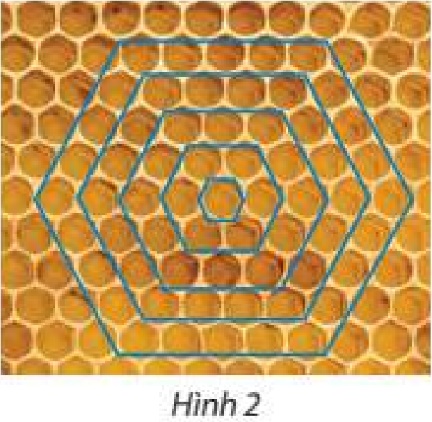
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.
Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
Ta có: Dãy số chỉ số ô trên các vòng là: \({u_1} = 6;{u_2} = 12;{u_3} = 18;...\)
Ta thấy: \({u_{n + 1}} = {u_n} + 6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai \({\rm{d}} = 6\).
Bình luận
Chia sẻ
- Giải mục 2 trang 54 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải mục 3 trang 54, 55 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 1 trang 56 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 2 trang 56 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Bài 3 trang 56 SGK Toán 11 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Biến cố hợp và quy tắc cộng xác suất - Toán 11 Chân trời sáng tạo
- Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện - Toán 11 Chân trời sáng tạo
- Lý thuyết Khoảng cách trong không gian - Toán 11 Chân trời sáng tạo
- Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Chân trời sáng tạo
- Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Chân trời sáng tạo
- Lý thuyết Biến cố hợp và quy tắc cộng xác suất - Toán 11 Chân trời sáng tạo
- Lý thuyết Biến cố giao và quy tắc nhân xác suất - Toán 11 Chân trời sáng tạo
- Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện - Toán 11 Chân trời sáng tạo
- Lý thuyết Khoảng cách trong không gian - Toán 11 Chân trời sáng tạo
- Lý thuyết Hai mặt phẳng vuông góc - Toán 11 Chân trời sáng tạo
