Toán 11, giải toán lớp 11 chân trời sáng tạo Bài 2. Biến cố hợp và quy tắc cộng xác suất Toán 11 Châ..

Lý thuyết Biến cố hợp và quy tắc cộng xác suất - Toán 11 Chân trời sáng tạo


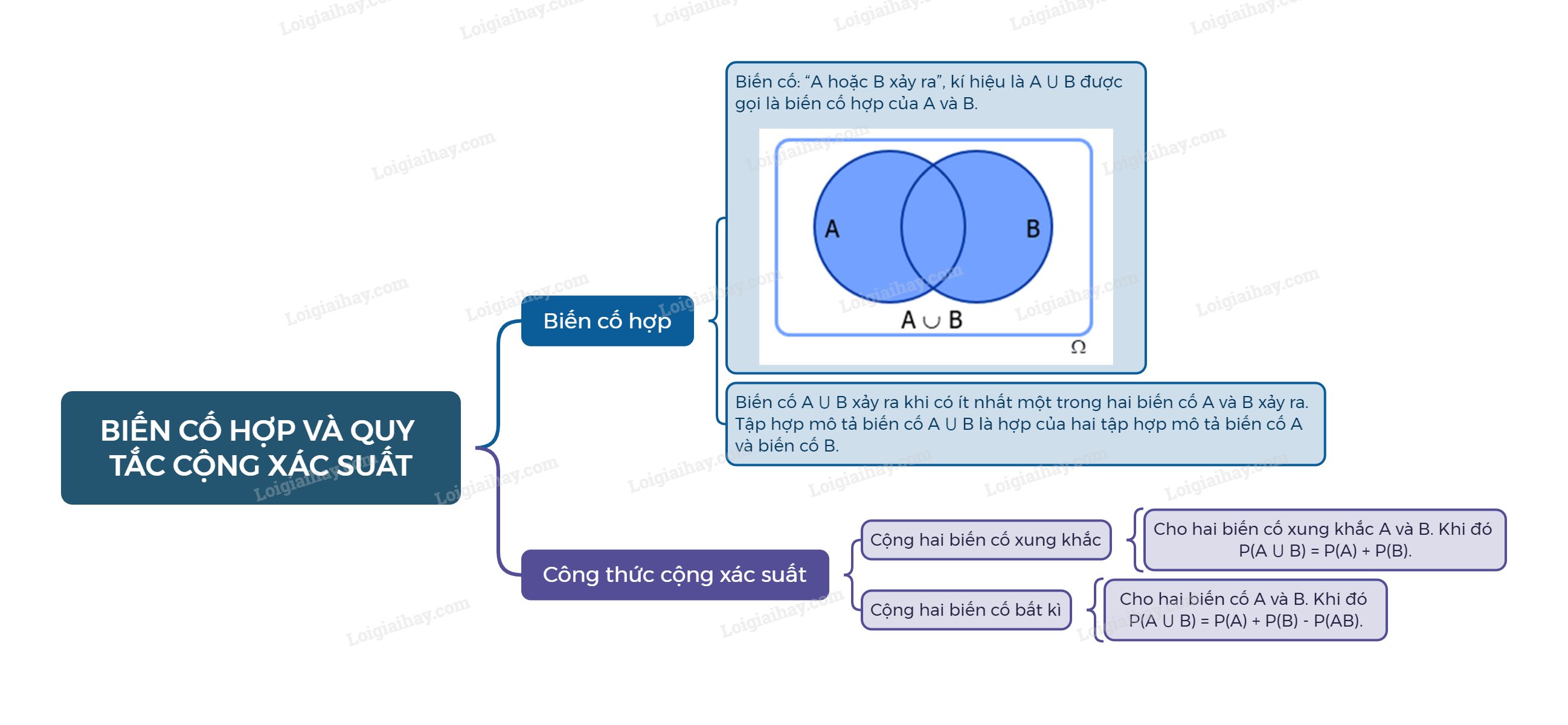
1. Biến cố hợp Cho hai biến cố A và B.

1. Biến cố hợp

Cho hai biến cố A và B. Biến cố: “A hoặc B xảy ra”, kí hiệu là \(A \cup B\) được gọi là biến cố hợp của A và B.

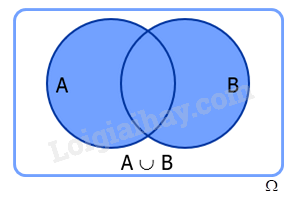
Chú ý: Biến cố \(A \cup B\) xảy ra khi có ít nhất một trong hai biến cố A và B xảy ra. Tập hợp mô tả biến cố \(A \cup B\) là hợp của hai tập hợp mô tả biến cố A và biến cố B.

2. Công thức cộng xác suất

Quy tắc cộng cho hai biến cố xung khắc:

Cho hai biến cố xung khắc A và B. Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\).

Quy tắc cộng cho hai biến cố bất kì:

Cho hai biến cố A và B. Khi đó \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store