Lý thuyết Góc giữa đường thẳng và mặt phẳng. Góc nhị diện - Toán 11 Chân trời sáng tạo

1. Góc giữa đường thẳng và mặt phẳng Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng \({90^0}\).

1. Góc giữa đường thẳng và mặt phẳng

Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng \({90^0}\).

Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).

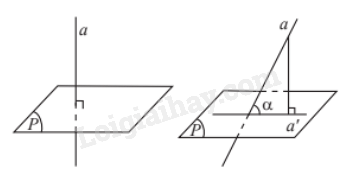
Chú ý:

a) Góc \(\alpha \) giữa đường thẳng và mặt phẳng luôn thỏa mãn \({0^0} \le \alpha \le {90^0}\).

b) Nếu đường thẳng a nằm trong (P) hoặc a song song với (P) thì \(\left( {a,\left( P \right)} \right) = {0^0}\).

2. Góc nhị diện và góc phẳng nhị diện

Góc nhị diện

Cho hai nửa mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\) có chung bờ là đường thẳng d. Hình tạo bởi \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) và d được gọi là góc nhị diện tạo bởi \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\), kí hiệu \(\left[ {{P_1},d,{Q_1}} \right]\).

Hai nửa mặt phẳng \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) gọi là hai mặt của nhị diện và d gọi là cạnh của nhị diện.

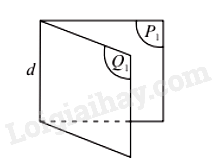
Chú ý:

a) Hai mặt phẳng cắt nhau theo giao tuyến d tạo thành bốn góc nhị diện.

b) Góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\) còn được kí hiệu là \(\left[ {M,d,N} \right]\) với M, N tương ứng thuộc hai nửa mặt phẳng \(\left( {{P_1}} \right),\left( {{Q_1}} \right)\).

Góc phẳng nhị diện

Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.

Chú ý:

a) Đối với một góc nhị diện, các góc phẳng nhị diện đều bằng nhau.

b) Nếu mặt phẳng (R) vuông góc với cạnh d của góc nhị diện và cắt hai mặt \(\left( {{P_1}} \right),\left( {{Q_1}} \right)\) của góc nhị diện theo hai nửa đường thẳng Ou và Ov thì \(\widehat {uOv}\) là góc phẳng nhị diện của góc nhị diện tạo bởi \(\left( {{P_1}} \right),\left( {{Q_1}} \right)\).

c) Góc nhị diện có góc phẳng nhị diện là góc vuông được gọi là góc nhị diện vuông.

d) Số đo góc phẳng nhị diện được gọi là số đo góc nhị diện.

e) Số đo góc nhị diện nhận giá trị từ \({0^0}\) đến \({180^0}\).