 Toán 11, giải toán lớp 11 chân trời sáng tạo
Toán 11, giải toán lớp 11 chân trời sáng tạo
 Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện ..
Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện ..
Giải mục 1 trang 82, 83 SGK Toán 11 tập 2 - Chân trời sáng tạo
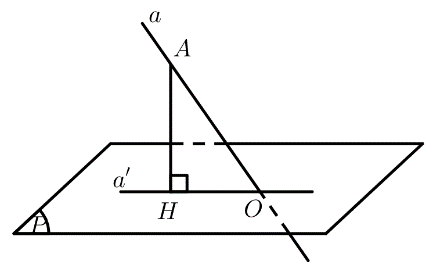
Cho đường thẳng (a) và mặt phẳng (left( P right)).
Hoạt động 1
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).
a) Trong trường hợp \(a\) vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và một đường thẳng \(b\) tuỳ ý trong \(\left( P \right)\).
b) Trong trường hợp \(a\) không vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và đường thẳng \(a'\) là hình chiếu vuông góc của \(a\) trên \(\left( P \right)\).
Phương pháp giải:
Sử dụng tính chất: Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^ \circ }\)
b) Lấy \(A \in a\). Gọi \(O = a \cap \left( P \right)\). Dựng \(AH \bot a'\left( {H \in a'} \right)\).
Ta có: \(\left( {a,a'} \right) = \left( {AO,OH} \right) = \widehat {AOH}\)
Thực hành 1
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa các đường thẳng sau đây với mặt phẳng \(\left( {ABCD} \right)\):
a) \(AA'\);
b) \(BC'\);
c) \(A'C\).
Phương pháp giải:
Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:
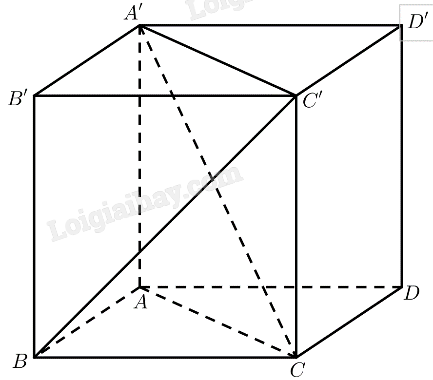
a) \(AA' \bot \left( {ABCD} \right) \Rightarrow \left( {AA',\left( {ABCD} \right)} \right) = {90^ \circ }\).
b) \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {BC',\left( {ABCD} \right)} \right) = \left( {BC',BC} \right) = \widehat {CBC'} = {45^ \circ }\)
c) \(AA' \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {ACA'}\)
\(\begin{array}{l}AC = AB\sqrt 2 = AA'\sqrt 2 \Rightarrow \tan \widehat {ACA'} = \frac{{AA'}}{{AC}} = \frac{{AA'}}{{AA'\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat {ACA'} \approx 35,{26^ \circ }\end{array}\)
Vậy \(\left( {A'C,\left( {ABCD} \right)} \right) \approx 35,{26^ \circ }\)
Vận dụng 1
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết \(AB = 1\,m,AD = 3,5{\rm{ }}m\). Tính góc giữa đường thẳng \(BD\) và đáy hồ.

Phương pháp giải:
Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:
\(DK \bot \left( {ABHK} \right) \Rightarrow \left( {B{\rm{D}},\left( {ABHK} \right)} \right) = \left( {B{\rm{D}},BK} \right) = \widehat {DBK}\)
\(DK = CH = 2,AK = \sqrt {A{{\rm{D}}^2} - D{K^2}} = \frac{{\sqrt {33} }}{2},KB = \sqrt {A{K^2} + A{B^2}} = \frac{{\sqrt {37} }}{2}\)
\(\tan \widehat {DBK} = \frac{{DK}}{{KB}} = \frac{4}{{\sqrt {37} }} \Rightarrow \widehat {DBK} \approx 33,{3^ \circ }\)
Vậy góc giữa đường thẳng \(BD\) và đáy hồ bằng \(33,{3^ \circ }\).
- Giải mục 2 trang 84, 85 SGK Toán 11 tập 2 - Chân trời sáng tạo
- Bài 1 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo
- Bài 2 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo
- Bài 3 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo
- Bài 4 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 136 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 130 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 121 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 113 SGK Toán 11 tập 1 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo












Danh sách bình luận