-
GIẢI SGK TOÁN 11 CHÂN TRỜI SÁNG TẠO - MỚI NHẤT
-
Toán 10 tập 1 - Chân trời sáng tạo
-
Toán 10 tập 2 - Chân trời sáng tạo
Toán 10, giải toán lớp 10 chân trời sáng tạo
Bài 1. Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra ..
Giải Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạo
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Thực hành 2 trang 89 SGK Toán 10 tập 2 – CTST
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
c) \(y = - {x^2}\)
d) \(y = 2{x^2} + 1\)
e) \(y = - \frac{1}{2}{x^2} + 4\)
Phương pháp giải - Xem chi tiết
Bước 1: Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
Bước 2: Tạo các thanh trượt biểu thị các tham số a, b, c bằng cách nhấp chuật liên tiếp vào thanh công cụ và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt (hình 4)
+) Nhập công thúc hàm số bậc hai \(y = a{x^2} + bx + c\) tại vùng nhập lệnh theo cú pháp: y = ax^2 + bx + c
+) Nhập công thức \(\Delta = {b^2} - 4ac\) bằng cách gõ: D = b^2 - 4ac
+) Quan sát đồ thị được vẽ trên vùng làm việc
+) Dùng chuột điều chỉnh các thanh trượt a, b, c để có giá trị mong muốn
+) Quan sát sự thay đổi của hình dạng đồ thị (parabol) và \(\Delta \) theo sự thay đổi các hệ số a, b, c trong công thức hàm số
Bước 3: Nêu kết luận về tính chất của đồ thị quan sát được trên hình vẽ
Lời giải chi tiết
Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
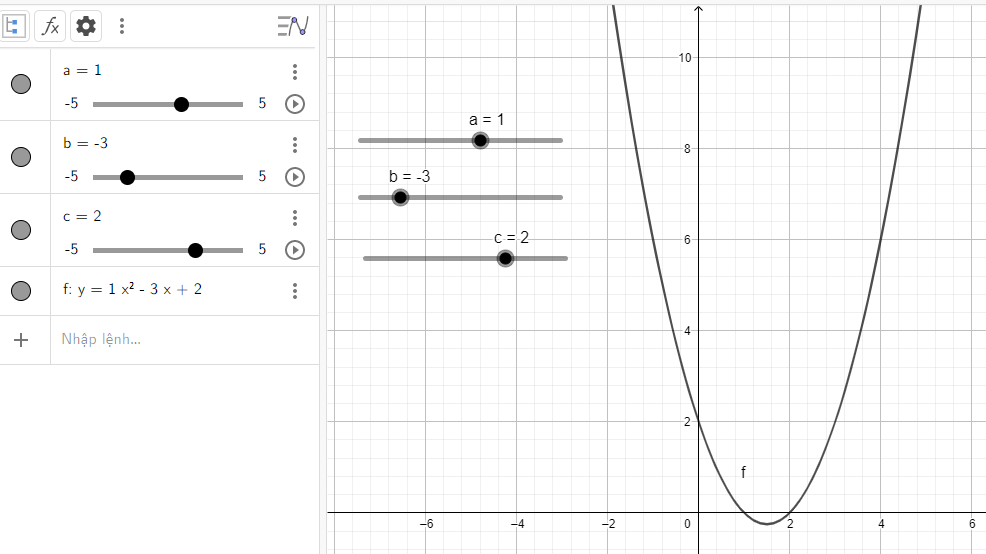
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
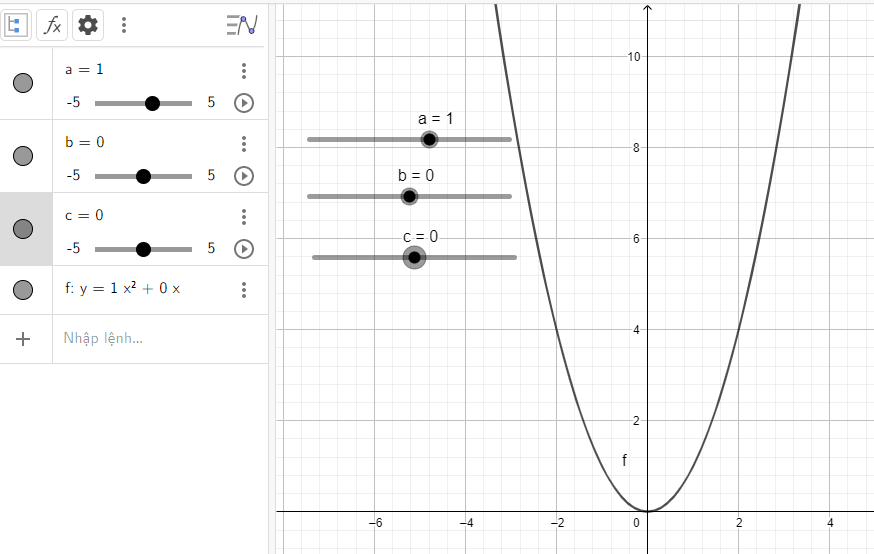
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
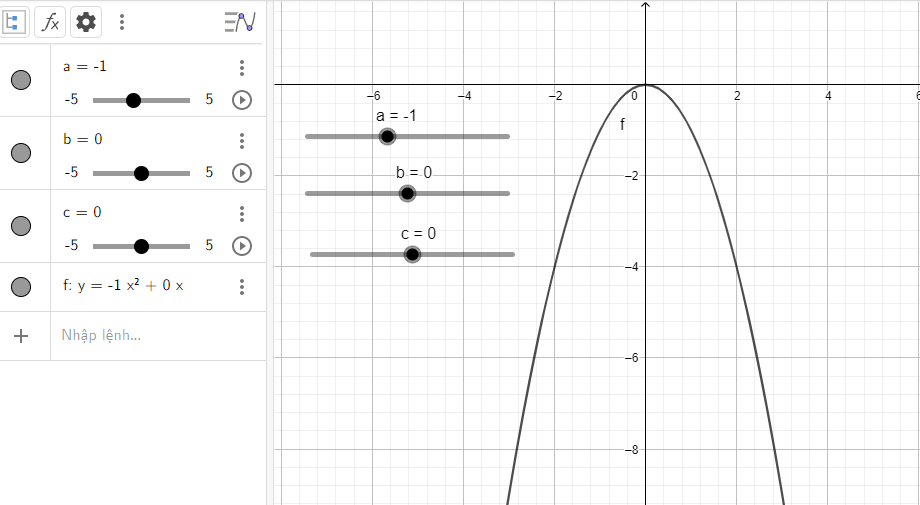
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
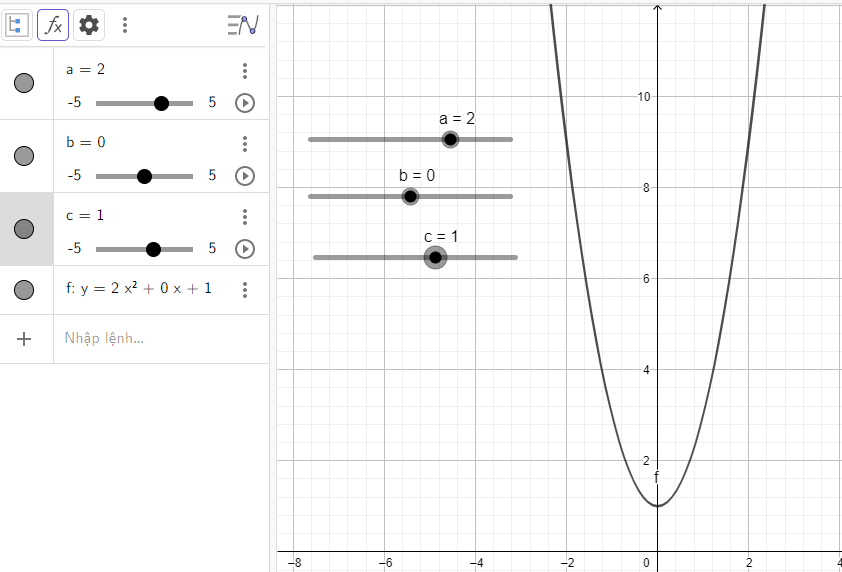
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải Hoạt động 3 trang 96 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 2 trang 94 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 3 trang 90 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 3 trang 96 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 2 trang 94 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 3 trang 90 SGK Toán 10 tập 2 - Chân trời sáng tạo
- Giải Hoạt động 2 trang 89 SGK Toán 10 tập 2 - Chân trời sáng tạo
