Bài 3.5, 3.6, 3.7, 3.8, 3.9, 3.10 trang 12,13 SBT Vật lí 10

3.5.

Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động thẳng nhanh dần đều \(v^2 –{v_0}^2 = 2as\), ta có các điều kiện nào dưới đây?

A. s > 0 ; a > 0 ; v > v₀.

B. s > 0 ; a < 0 ; v < v₀.      

C. s > 0 ; a > 0 ; v < v₀.

D. s > 0 ; a < 0 ; v > v₀.

Phương pháp giải:

Áp dụng công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động thẳng nhanh dần đều \(v^2 –{v_0}^2 = 2as\), trong đó \(s > 0\); \(a > 0\); \(v > v_0\).

Lời giải chi tiết:

Vì công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động thẳng nhanh dần đều \(v^2 –{v_0}^2 = 2as\), trong đó \(s > 0\); \(a > 0\); \(v > v_0\).

Chọn đáp án A

3.6.

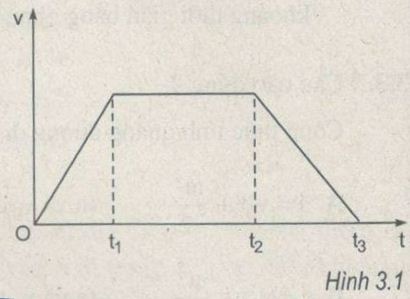
Hình 3.1 là đồ thị vận tốc theo thời gian của một xe máy chuyển động trên một đường thẳng. Trong khoảng thời gian nào, xe máy chuyển động chậm dần đều?

A. Trong khoảng thời gian từ 0 đến t₁ .

B. Trong khoảng thời gian từ t₁ đến t_2 .

C. Trong khoảng thời gian từ t₂ đến t_3 .

D. Các câu trả lời A, B, C đều sai.

Phương pháp giải:

Sử dụng lí thuyết về chuyển động thẳng chậm dần đều:

- Vận tốc giảm dần theo thời gian

- Đồ thị vận tốc theo thời gian là đường thẳng xiên góc đi xuống

Lời giải chi tiết:

+ Trong khoảng thời gian \(0\) đến \(t_1\) xe máy chuyển động nhanh dần đều.

+ Trong khoảng thời gian \(t_1\) đến \(t_2\) xe máy chuyển động thẳng đều.

+ Trong khoảng thời gian \(t_2\) đến \(t_3\) xe máy chuyển động chậm dần đều.

Vì trong khoảng thời gian từ t₂ đến t₃: đồ thị vận tốc theo thời gian là đường thẳng xiên góc đi xuống _.

Chọn đáp án C

3.7.

Khi ô tô đang chạy với vận tốc \(10 m/s\) trên đoạn đường thẳng thì người lái xe tăng ga và ô tô chuyển động nhanh dần đều. Sau \(20 s\), ô tô đạt vận tốc \(14  m/s\). Gia tốc a và vận tốc v của ô tô sau \(40 s\) kể từ lúc bắt đầu tăng ga là bao nhiêu?

A. a = 0,7 m/s² ; v = 38 m/s.

B. a = 0,2 m/s² ; v = 18 m/s.   

C. a = 0,2 m/s² ; v = 8 m/s.

D. a = 1,4 m/s² ; v = 66 m/s.

Phương pháp giải:

Áp dụng công thức: \(v = {v_0} + at\)

Lời giải chi tiết:

Ta có: \(v = {v_0} + at\) \( \to a = \dfrac{{v - {v_0}}}{t}\)

Sau khoảng thời gian \(\Delta t = 20s\) kể từ thời điểm ban đầu: \(a = \dfrac{{14 - 10}}{{20}} = 0,2(m/{s^2})\)

Ta suy ra phương trình vận tốc: \(v=10+0,2t\) \(m/s\)

Tại \(t = 40s\) vận tốc của xe là \(v = 10 + 0,2.40 = 18(m/s)\)

Chọn đáp án B

3.8.

Cũng bài toán trên, hỏi quãng đường \(s\) mà ô tô đã đi được sau \(40 s\) kể từ lúc bắt đầu tăng ga và tốc độ trung bình \(v_{tb}\) trên quãng đường đó là bao nhiêu?

A. s = 480 m ; v_tb = 12 m/s.

B. s = 360 m ; v_tb = 9 m/s.

C. s = 160 m ; v_tb = 4 m/s.

D. s = 560 m ; v_tb = 14 m/s.

Phương pháp giải:

- Áp dụng công thức liên hệ: \({v^2} - v_0^2 = 2aS\)

- Áp dụng công thức tính vận tốc trung bình: \({v_{tb}} = \dfrac{S}{t}\)

Lời giải chi tiết:

Quãng đường mà người đó đã đi được sau \(40 s\) là:

\({v^2} - v_0^2 = 2aS \\\to S = \dfrac{{{v^2} - v_0^2}}{{2a}}\\ = \dfrac{{{{18}^2} - {{10}^2}}}{{2.0,2}} = 560(m)\)

Vận tốc trung bình của người đó là: 

\({v_{tb}} = \dfrac{S}{t} = \dfrac{{560}}{{40}} = 14(m/s)\)

Chọn đáp án D

3.9.

Khi ô tô đang chạy với vận tốc 10 m/s trên đoạn đường thẳng thì người lái xe hãm phanh và ô tô chuyển động chậm dần đều. Cho tới khi dừng hẳn lại thì ô tô đã chạy thêm được 100 m. Gia tốc a của ô tô là bao nhiêu ?

A. a = -0,5 m/s².            C. a = -0,2 m/s².

B. a = 0,2 m/s² .            D. a = 0,5 m/s².

Phương pháp giải:

Áp dụng công thức liên hệ: v² – v₀² = 2as

Lời giải chi tiết:

Ta có:

\({v^2} - v_0^2 = 2aS \\\to a = \dfrac{{{v^2} - v_0^2}}{{2S}}\\= \dfrac{{{0^2} - {{10}^2}}}{{2.100}} =  - 0,5(m/{s^2})\)

Chọn đáp án A

3.10*.

Một ô tô xuống đốc nhanh dần đều không vận tốc đầu. Trong giây thứ 5 nó đi được 13,5 m. Gia tốc của ô tô là:

A. \(3(m/{s^2})\)

B. \(1,08(m/{s^2})\)

C. \(27(m/{s^2})\)

D. \(2,16(m/{s^2})\)

Phương pháp giải:

Áp dụng công thức tính quãng đường vật đi được trong chuyển động thẳng biên đổi đều: \(S = {v_0}t + \dfrac{1}{2}a{t^2}\)

Lời giải chi tiết:

Vì xe xuống dốc không vận tốc đầu nên \({v_0} = 0\) \( \to S = \dfrac{1}{2}a{t^2}\)

Quãng đường xe đi được sau 5s là: \({S_5} = \dfrac{1}{2}a{.5^2}\)

Quãng đường xe đi được sau 4s là: \({S_4} = \dfrac{1}{2}a{.4^2}\)

Suy ra quãng đường xe đi được trong giây thứ 5 là: \(\Delta S = {S_5} - {S_4} \\= \dfrac{1}{2}a{.5^2} - \dfrac{1}{2}a{.4^2} = 4,5a\)

\( \to \Delta S = 4,5a = 13,5m\)

Vậy gia tốc a của xe là: \(a = \dfrac{13,5}{4,5} = 3(m/{s^2})\)

Chọn đáp án A

Loigiaihay.com