Giải Bài 100 trang 98 sách bài tập toán 7 - Cánh diều

Cho tam giác ABC có \(\widehat {BAC} = 110^\circ \). Các đường trung trực của AB và AC cắt cạnh BC lần lượt tại E và F. Khi đó, số đo góc EAF bằng:

Đề bài

Cho tam giác ABC có \(\widehat {BAC} = 110^\circ \). Các đường trung trực của AB và AC cắt cạnh BC lần lượt tại E và F. Khi đó, số đo góc EAF bằng:

A. 20°;

B. 30°;

C. 40°;

D. 50°.

Phương pháp giải - Xem chi tiết

Sử dụng tổng số đo các góc trong tam giác và tam giác cân, đường trung trực của tam giác để tính số đo góc EAF

Lời giải chi tiết

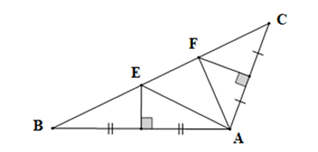
Xét tam giác ABC có:

\(\hat B + \hat C + \widehat {BAC} = 180^\circ \) (tổng ba góc trong một tam giác)

Suy ra \(\hat B + \hat C = 180^\circ - \widehat {BAC} = 180^\circ - 110^\circ = 70^\circ \)

Vì E thuộc đường trung trực của AB nên EB = EA.

Do đó tam giác ABE cân tại E nên \(\widehat {EAB} = \hat B\)

Vì F thuộc đường trung trực của AC nên FC = FA.

Do đó tam giác ACF cân tại F nên \(\widehat {F{\rm{A}}C} = \hat C\)

Ta có \(\widehat {BA{\rm{E}}} + \widehat {E{\rm{A}}F} + \widehat {FAC} = \widehat {BAC}\)

Hay \(\hat B + \widehat {E{\rm{A}}F} + \hat C = \widehat {BAC}\)

Do đó \(\widehat {E{\rm{A}}F} = \widehat {BAC} - \left( {\hat B + \hat C} \right)\)

Suy ra \(\widehat {E{\rm{A}}F} = 110^\circ - 70^\circ = 40^\circ \).

Vậy ta chọn đáp án C.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải Bài 101 trang 98 sách bài tập toán 7 - Cánh diều
Trong các hình 62a, 62b, 62c, 62d, hình nào có điểm cách đều các đỉnh của tam giác đó? Vì sao?
Giải Bài 102 trang 98 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC và điểm G nằm trong tam giác. Chứng minh: Nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.
Giải Bài 103 trang 98 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có ba góc nhọn, AB < AC < BC. Các tia phân giác của góc A và góc C cắt nhau tại O. Gọi F là hình chiếu của O trên BC; H là hình chiếu của O trên AC. Lấy điểm I trên đoạn FC sao cho FI = AH. Chứng minh:
Giải Bài 104 trang 99 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có AB < AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA.
Giải Bài 105 trang 99 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC cân tại A có các đường cao BD và CE cắt nhau tại H.
Giải Bài 106 trang 99 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC vuông tại A có AB < AC. Vẽ AD là tia phân giác của góc BAC (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB.
Giải Bài 99 trang 98 sách bài tập toán 7 - Cánh diều
Cho hai tam giác ABC và MNP có \(\widehat {ACB} = \widehat {MPN}\), \(\widehat {ACB} = \widehat {MPN}\). Cần thêm một điều kiện để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc – cạnh – góc là: